Second
- 2. Jika diberikan suatu barisan aritmatika melalui blog support, siswa kelas XI jurusan pertanian akan dapat: 1. menentukan suku ke-n barisan tersebut dengan benar. 2. menghitung jumlah n suku deret tersebut dengan benar Menerapkan konsep barisan dan deret aritmatika Menerapkan konsep barisan dan deret dalam pemecahan masalah
- 3. PERHATIKAN PERMASALAHAN BERIKUT. Seorang pemilik kebun memetik jeruk setiap hari dan mencatatnya. Ternyata banyak jeruk yang dipetik pada hari pertama 100 buah, hari kedua 120 buah, hari keempat 140 buah, dan seterusnya. Berapakah jeruk yang dipetik pada hari ketujuh?
- 4. Banyak buah jeruk yang dipetik setiap hari adalah 100, 120, 140, . . . Selisish banyak buah jeruk yang dipetik setiap hari adalah konstan , yaitu 20. Barisan bilangan yang mempunyai ciri seperti itu disebut BARISAN ARITMATIKA. Selisih dua bilangan yang berurutan disebut BEDA (b) Bilangan-bilangan pada urutan bilangan disebut SUKU (Un)
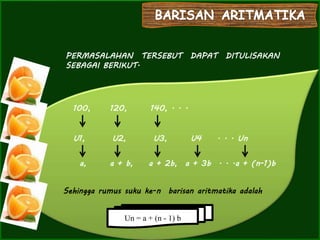
- 5. ooooooooooooooooooooooooo ooooo100, 120, 140, . . . PERMASALAHAN TERSEBUT DAPAT DITULISAKAN SEBAGAI BERIKUT. U1, U2, U3, U4 . . . Un a, a + b, a + 2b, a + 3b . . .a + (n-1)b Sehingga rumus suku ke-n barisan aritmatika adalah Un = a + (n - 1) b
- 6. ooooooooooooooooooooooooo ooooo Sehingga banyak jeruk yang dipetik pada hari ke-7 dapat dihitung sebagai berikut. a = 100 b = 20 n = 7 Jadi banyak jeruk yang dipetik pada hari ketujuh sebanyak 220 buah U7 = 100 + (7 – 1) 20 U7 = 100 + (6) 20 U7 = 100 + 120 U7 = 220 Un = a + (n - 1) b
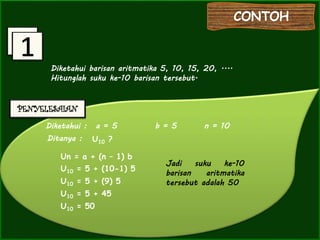
- 7. ooooooooooooooooooooooooo ooooo Diketahui barisan aritmatika 5, 10, 15, 20, .... Hitunglah suku ke-10 barisan tersebut. a = 5 b = 5 n = 10 Jadi suku ke-10 barisan aritmatika tersebut adalah 50 Diketahui : Ditanya : U10 ? Un = a + (n – 1) b U10 = 5 + (10-1) 5 U10 = 5 + (9) 5 U10 = 5 + 45 U10 = 50
- 8. ooooooooooooooooooooooooo ooooo Diketahui barisan aritmatika dengan U6 = 50 dan U41 = 155. Tentukan suku pertama barisan tersebut! U6 = 50 50 = a + 5b U41 = 155 155 = a + 40b X 8 155 = a + 40b 400 = 8a + 40b X 1 - 245 = 7a 245/7 = a 35 = a Jadi suku pertama barisan tersebut adalah 35
- 9. INGAT KEMBALI PERMASALAHAN PADA BARISAN ARITMATIKA BERIKUT. Seorang pemilik kebun memetik jeruk setiap hari dan mencatatnya. Ternyata banyak jeruk yang dipetik pada hari pertama 100 buah, hari kedua 120 buah, hari keempat 140 buah, dan seterusnya. Berapakah jeruk yang terkumpul selama sepuluh hari pertama?
- 10. Untuk mengetahui jeruk yang terkumpul selama sepuluh hari pertama adalah dengan menjumlahkan banyak jeruk setiap harinya. 100 + 120 + 140 + . . . U1 + U2 + U3 + . . . + U10 Jumlah beruntun suku-suku barisan aritmatika disebut deret aritmatika Jumlah n suku pertama deret aritmatika dilambangkan dengan Sn
- 11. Sn = U1 + U2 + U3 + . . . + Un-2 + Un-1 + Un Jika Sn persamaan 1 di atas dibalik maka didapatkan Sn sebagai berikut. Sehingga : Sn = a + (a+b) + (a+2b) + (a+3b) + . . . + (Un-2b) + (Un-b) + Un Persamaan 1 Sn = Un + (Un-b) + (Un-2b) + . . . + (a+3b) + (a+2b) + (a+b) + a Persamaan 2 Jika persamaan 1 dan persamaan 2 di atas dijumlahkan akan didapatkan persamaan berikut.
- 12. Jiadi jumlah n suku pertama suatu deret aritmatika adalah Lanjutan 2Sn = (a+Un)+(a+Un)+(a+Un)+ . . . +(a+Un)+(a+Un)+(a+Un) 2Sn = n (a+Un) Sn = n/2 (a+Un) Sn = n/2 (a + Un)
- 13. Sehingga untuk mengetahui jumlah jeruk yang terkumpul pada sepuluh hari pertama dapat dihitung sebagai berikut: Sn = n/2 (a + Un) a = 100 b = 20 U10 = a + (10 - 1) b = 100 + (9) 20 = 280 S10 = 10/2 (100 + 280) S10 = 5 (380) S10 = 1900 Jadi jeruk yang terkumpul selama 10 hari pertama adalah 1900 buah
- 14. ooooooooooooooooooooooooo ooooo Hitunglah jumlah sepuluh suku pertama deret aritmatika 11 + 16 + 21 + . . . a = 11 b = 5 n = 10Diketahui : Ditanya : S10 ? U10 = a + 9b U10 = 11 + (9) 5 U10 = 11 + 45 U10 = 56 Sn = ½ n (a + Un) S10 = ½ 10 (11 + 56) S10 = ½ 10 (67) S10 = 335 Jadi jumlah sepuluh suku pertama deret aritmatika tersebut adalah 50
- 15. ooooooooooooooooooooooooo oooooU5 = 40 40 = a + 4b U8 = 25 25 = a + 7b X 7 100 = 4a + 28b 280 = 7a + 28b X 4 - 180 = 3a 180/3 = a Jadi jumlah delapan suku pertama deret aritmatika tersebut adalah 340 Suku ke-5 suatu deret aritmatika adalah 40 dan suku ke-8 deret itu adalah 25. Hitunglah jumlah sepuluh suku pertama deret tersebut! S8 = ½ 8 (60 + 25) 60 = a S8 = ½ n (a + U8) = 4 (85)= 340