Section 3: Interpreting Sensitivity Analysis on Excel Solver
- 1. By: Zakaria Elsayed Hasaneen Teaching Assistant at Faculty of Commerce Accounting Department (English Section) Kafrelsheikh University OR Section (3) Interpreting Sensitivity Analysis on Excel Solver Grade 4 ŌĆōTerm 2 Zakaria Hasaneen Zakaria Hasaneen Zakaria Hasaneen
- 2. Interpreting Excel's Solver Report Max 50A + 60B + 55C s.t. A + B + C Ōēż 100 2A + 3B + 2C Ōēż 300 2A + 3B + 2C Ōēź 250 A + 2C Ōēź 60 A,B,C Ōēź0
- 4. Required 1. State the optimal solution 2. What is the optimal objective function value? 3. What would happen to the optimal solution if a) the unit profit on B decreases by 20? b) the unit profit on C decreases to 45? c)the unit profits on A & C change to 53 (Simultaneous Changes-100% Rule)? 4. Interpret the reduced cost for A 5. What would happen to the objective function if a) the RHS of constraint 1 increases by 5? b) the RHS of constraint 2 decreases to 250? c) the RHS of constraint 4 changes to 44? 6. What are the slack/surplus values? 7. Which constraints are binding?
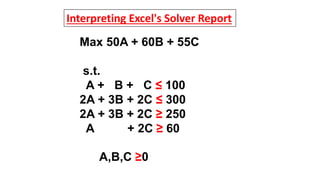
- 5. (1)
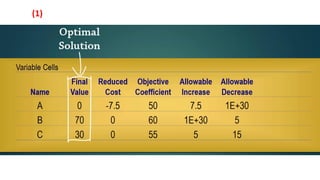
- 6. (2)
- 7. Now, these Allowable Increase & Decrease values specify how much the objective coefficients can change before the optimal solution will change. BEFORE WE SOLVE POINT #3 ,WE SHOULD KNOW :
- 8. For example, since the Allowable Increase for A is 7.5, if we increase the objective coefficient of A, from 50 to any value, up to an upper limit of 57.5, the optimal solution will not change. For the Allowable Decrease, Excel usually represents very large values with 1E+30. So you can think of it as infinity. Thus the lower limit for the coefficient of A is negative infinity.
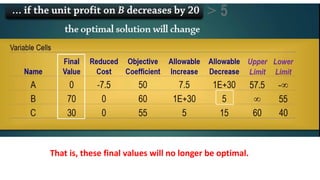
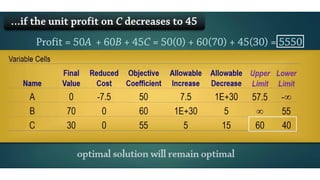
- 9. (3) A- So what will happen to the optimal solution if the unit profit on B (that is, the coefficient) decreases by 20? We can see here that the Allowable Decrease on B is 5. Therefore, the optimal solution will change if we decrease it by 20.
- 10. That is, these final values will no longer be optimal.
- 11. (3) B-
- 13. (3) C-
- 16. (4) The reduced cost of -7.5 here represents the amount by which profit will be reduced if we include a unit of A in the solution.
- 17. so, product A is not attracting enough profit to warrant its inclusion in the product mix. To include product A (or to make A positive), itŌĆÖs profit contribution needs to improve by at least 7.5. But at its current value of 50, making A positive in the optimal solution will bring a reduction of 7.5 to Profit, per unit.
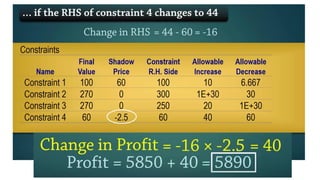
- 18. 5- What would happen to the objective function if a) the RHS of constraint 1 increases by 5? b) the RHS of constraint 2 decreases to 250? c)the RHS of constraint 4 changes to 44? Requirement:
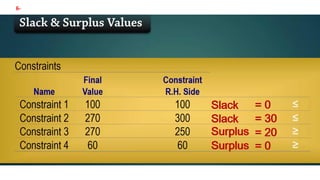
- 24. 6-
- 25. 7.