section-7.ppt
Download as PPT, PDF
0 likes8 views
- Horst Feistel devised the Feistel cipher structure, which partitions the plaintext input block into two halves, and processes them through multiple rounds of substitution and permutation. - Virtually all modern block ciphers, including the Data Encryption Standard (DES), are based on the Feistel cipher structure. Each round performs a substitution on one half of the data using a round function combined with a subkey. - Simplified DES (S-DES) is a simplified version of DES that operates on an 8-bit plaintext block and uses a 10-bit key. It involves an initial permutation, two complex functions fk using substitution and permutation dependent on subkeys, and a final inverse permutation.
section-7.ppt
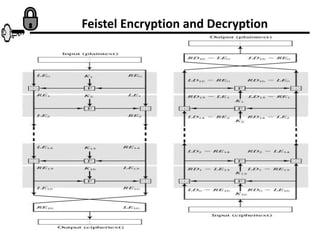
- 1. Feistel Cipher Structure Horst Feistel devised the feistel cipher based on concept of invertible product cipher partitions input block into two halves process through multiple rounds which: perform a substitution on left data half based on round function of right half & sub key then have permutation swapping halves implements Shannons substitution-permutation network concept
- 2. Feistel Cipher Structure (1973) Virtually all conventional block encryption algorithms including data encryption standard (DES) are based on Feistel Cipher Structure. The plaintext is divided into two halves Then the two halves pass through n rounds of processing then combine to produce the cipher block. Each round has as input and derived from the previous round as well as a sub-key derived from the overall 0 0 and R L i K K i i 1 i L 1 i R
- 3. Feistel Cipher Structure (1973) All rounds have the same structure A substitution is performed on the left half of the data. This is done by applying a round function to the right half of the data followed by the XOR of the output of that function and the left half of the data. F
- 6. Design Features of Feistel Network Block Size: (larger block means greater security) 64 bits. Key Size:56-128 bits. Number of Rounds: a single round offers inadequate security, a typical size is 16 rounds. Sub-key Generation Algorithms: greater complexity should lead to a greater difficulty of cryptanalysis. Round function: Again, greater complexity generally means greater resistance to cryptanalysis.
- 7. Design Features of Feistel Network . Round function: Again, greater complexity generally means greater resistance to cryptanalysis. Fast Software encryption/Decryption: the speed of execution of the algorithm is important. Ease of Analysis: to be able to develop a higher level of assurance as to its strength Decryption: use the same algorithm with reversed keys.
- 8. Feistel Encryption and Decryption
- 9. Simplified DES (S-DES) Developed by Prof. Edward Schaefer of Santa Clara University 1996. Takes 8 bit block of plain text and 10 bit key as input and produce an 8 bit block cipher text output. The encryption algorithm involves 5 functions: initial permutation (IP); a complex function fk which involves substitution and permutation depends on the key; simple permutation function (switch) SW; the function fk again and final inverse of the initial permutation( IP-1).
- 11. Overview We can express the encryption algorithm as a composition function: IP-1fk2 SW fk1 IP OR ; Ciphertext=IP-1(fk2(SW(fk1(IP(plaintext))))) Where, K1=P8(shift(P10(key))) K2 =P8 (shift(shift(P10(key)))) The decryption algorithm is: Plaintext=IP-1 (fk1(SW(fk2(IP(Ciphertext)))))
- 12. Key Generation for S-DES
- 13. Key Generation for S-DES First permute the key in the following way: Ex: (1010000010)is permuted to (1000001100) Perform a circular left shift to each bits of the key: Ex: (1000001100)(0000111000) Next apply P8 This yields K1=(10100100) P10 3 5 2 7 4 10 1 9 8 6 P8 6 3 7 4 8 5 10 9
- 14. Continue Then perform again 2 bit circular shift left on each of the five bits: (00001)(11000)(00100)(00011) Finally apply again P8: Then K2=(01000011)
- 15. S-DES Encryption
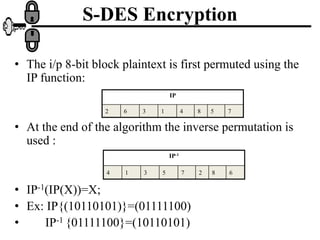
- 16. S-DES Encryption The i/p 8-bit block plaintext is first permuted using the IP function: At the end of the algorithm the inverse permutation is used : IP-1(IP(X))=X; Ex: IP{(10110101)}=(01111100) IP-1 {01111100}=(10110101) IP 2 6 3 1 4 8 5 7 IP-1 4 1 3 5 7 2 8 6
- 17. The Function fk Let L and R be the left most 4 bits and rightmost 4 bits of the 8 bits input fk (L, R)=(LF(R,SK),R) Where SK is a sub key and the is bit-by-bit XOR function. Ex: if the o/p of the IP is (10111101) and F(1101,SK)=(1110) for some SK then fk(10111101)=(1011) (1110)=(0101)
- 18. Continue Recall the first operation is an expansion and permutation to first 4 bits as follows: We can depict the result as : The 8 bit key K1is added to this value using XOR: E / P 4 1 2 3 2 3 4 1 n4 n1 n2 n3 n2 n3 n4 n1 n4+K11 n1+ K12 n2 +K13 n3 +K14 n2 +K15 n3 +K16 n4 +K17 n1 +K18
- 19. Continue Let us rename these bits: The first row of the matrix 4 bits are fed into the S- box S0 to produce 2 bit o/p and the remaining 2 bits are fed to S1 to produce another 2 bits P0,0 P0,1 P0,2 P0,3 P1,0 P1,1 P1,2 P1,3
- 20. S-Box The s-box operates as follows: (P0,0,P0,3 ) determine the row of the S0 matrix and (P0,1,P0,2 )determine the column: Ex: if (P0,0,P0,3 ) =(00), (P0,1,P0,2 )=(10) then the o/p is from row 0 and column 2 in S0 which is equal to 3, i.e., (11) in binary. In a similar way we can produce the other two bits 3 0 1 2 0 1 0 3 3 1 0 2 3 2 1 0 1 , 2 3 1 3 3 1 2 0 0 1 2 3 2 3 0 1 0 S S
- 21. The Switch Function (SW) SW interchange the left and right 4 bits so that the second instance of fK operates on a different 4 bits.