Seminar On Kalman Filter And Its Applications
9 likes4,809 views
The document discusses Kalman filters and their applications. It provides an overview of Kalman filters, explaining that they are used to estimate unknown system states from measurements that contain errors. It describes the basic algorithmic steps of Kalman filters, including prediction to project the state ahead and correction to incorporate new measurements. Finally, it gives examples of applications, such as for channel estimation in direct sequence spread spectrum communication systems.
Seminar On Kalman Filter And Its Applications
- 1. Seminar on Kalman Filter and its applications Presented by: Ms. Barnali Dey M.Tech (DEAC) SMIT
- 2. Overview The Problem Why do we need Kalman Filters? What is a Kalman Filter? Alogorithmic steps of Kalman Filter Applications
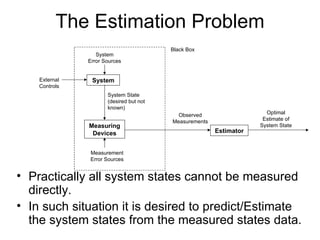
- 3. The Estimation Problem Practically all system states cannot be measured directly. In such situation it is desired to predict/Estimate the system states from the measured states data. Measuring Devices Estimator Measurement Error Sources System State (desired but not known) External Controls Observed Measurements Optimal Estimate of System State System Error Sources System Black Box
- 4. What is a Kalman Filter? Recursive data processing algorithm Generates optimal estimate of desired quantities given the set of measurements Optimal? For linear system and white Gaussian errors, Kalman filter is best estimate based on all previous measurements Recursive? Doesnt need to store all previous measurements and reprocess all data each time step
- 5. Algorithm for discrete-time Kalman Filter Given system model in state space in discrete time Given measurement equation
- 6. For recursive algorithm to work, set following initial conditions Estimation of states by Kalman Filter implementation has two main steps: Prediction also called time update Correction also called measurement update Set to very small value Set to high value
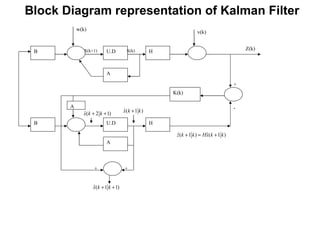
- 7. Theoretical Basis Prediction (Time Update) (1) Project the state ahead (2) Project the error covariance ahead Correction (Measurement Update) (2) Compute the Kalman Gain (3) Correct the estimate with measurement z(k+1) (4) Update Error Covariance matrix (1) Observe new measurement at (k+1)th instant Correction term
- 8. Block Diagram representation of Kalman Filter B U.D H B U.D H A A K(k) A Z(k) v(k) w(k) X(k+1) X(k) + - + +
- 9. Application DSSS ( direct sequence spread spectrum) communication DSSS communication is widely applied in various wireless communication scenarios in which both severe frequency selective multi-path and narrowband interference may occur simultaneously. To receive DSSS signal, we should k now : code delay to obtain pseudo-noise (PN) code synchronization coefficients of multi-path channel narrowband interference. Thus, it becomes necessary to jointly estimate code delay, multi-path channel and narrowband interference parameters in DSSS receiver
- 10. General Channel Estimation Procedure
- 11. Why Channel Estimation ? Allows the receiver to approximate the effect of the channel on the signal. The channel estimate is essential for removing inter symbol interference, noise rejection techniques etc. Also used in diversity combining, ML detection, angle of arrival estimation etc.
- 12. Types of Channel Estimation Methods There Are two Basic types of Channel Estimation Methods: Training Sequence methods Blind Methods
- 13. Algorithm Overview Consider a radio communications system using training sequences to do channel estimation. We use a method of improving on the training sequence based estimate. Additional feature(Jakes Model): Under certain assumptions we can adopt the Jakes model for the channel. This allows us to have a second estimate independent of the data based (training sequence) estimate. The Kalman estimation algorithm uses these two independent estimates of the channel to produce an estimate. The Kalman filter based channel estimator leads to a significant gain in performance as compared to the data-only estimator.