Shannon’s strategy
- 1. Shannon’s strategy • thwart cryptanalysis that is based on statistical analysis • hacker has some knowledge of statistical characteristic of plaintext • if statistics are reflected in ciphertext, then analyst may be able to deduce encryption key, or part of it • In Shannon’s ideal cipher, statistics of ciphertext are independent of plaintext
- 2. Shannon’s building blocks confusion make relation between statistics of ciphertext and the value of the encryption key as complex as possible diffusion diffuse statistical property of plaintext digit across a range of ciphertext digits i.e. each plaintext digits affects value of many ciphertext digits
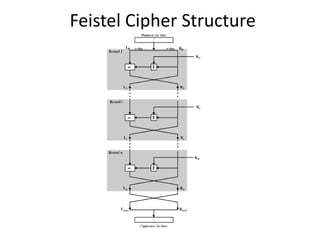
- 3. Feistel cipher • input plaintext of 2w bits • key K = n sub-keys: K1, K2, …, Kn • The plain text is divided into 2 halves Lo and Ro • sequence of n “rounds” each using Ki • substitution followed by a permutation • apply function F(Ki) to right half of data, then exclusive-OR it to left half of data • permutation: interchange two result halves of data • Li+1=Ri Ri+1=Li F(Li+1,Ki)
- 5. Feistel Cipher Design Principles • block size – increasing size improves security, but slows cipher • key size – increasing size improves security, makes exhaustive key searching harder, but may slow cipher • number of rounds – increasing number improves security, but slows cipher • subkey generation – greater complexity can make analysis harder, but slows cipher • round function – greater complexity can make analysis harder, but slows cipher • fast software en/decryption & ease of analysis – are more recent concerns for practical use and testing
- 6. Feistel Cipher Encryption and Decryption
- 7. Decryption • Ri=Li+1 Li=Ri+1 F(Li+1,Ki)