SICP
- 1. SICP 二章 2013年 7月 2.1.1-2.1.4
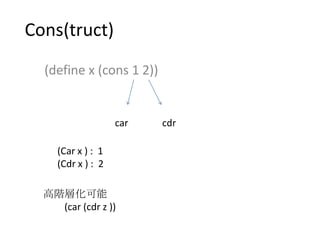
- 2. Cons(truct) (define x (cons 1 2)) car cdr 高階層化可能 (car (cdr z )) (Car x ) : 1 (Cdr x ) : 2
- 4. ラムダ計算 非形式的な概説 (wiki) 例えば、ある数に 2 を加える関数 f を考える。これは通常の書き方では f(x) = x + 2 と書くことができるだろう。この関数 f は、ラムダ計算の式 (ラムダ式という)では λx. x + 2 と書かれる。変数 x の名前は重要では なく、 λy. y + 2 と書いても同じである。同様に、この関数に 3 を適用し た結果の数 f(3) は (λx. x + 2) 3 と書かれる。関数の適用は左結合である。 つまり、 f x y = (f x) y である。今度は、引数(関数の入力)に関数をとり それに 3 を適用する関数を考えてみよう。これはラムダ式では λf. f 3 と なる。この関数に、先ほど作った 2 を加える関数を適用すると、 (λf. f 3) (λx. x + 2) となる。ここで、 (λf. f 3) (λx. x + 2) と (λx. x + 2) 3 と 3 + 2 の3つの表現はいずれも同値である。
- 5. Church数 (wikipedia) 0 ≡ λf.λx. X 1 ≡ λf.λx. f x 2 ≡ λf.λx. f (f x) 3 ≡ λf.λx. f (f (f x))... n ≡ λf.λx. fn x... 直感的には、数 n はラムダ式では f という関数 をもらってそれを n 回適用したものを返す関数 である。つまり、チャーチ数は1引数関数を受け 取り、1引数関数を返す高階関数である。
- 6. Church数 ○n+1 n を受け取って n + 1 を返す関数を定 義することができる。 SUCC := λn f x. f (n f x)
- 7. Church数 ○掛け算 m*n MULT := λm n. m (PLUS n) 0 この定義は、 m と n の乗算は、 0 に n を m回 加えることと等しい、ということを利用して 作られている。 MULT := λm n f. m (n f)
- 8. 問 2.5 (define (print-point p) (newline) (display "(") (display (car p)) (display ",") (display (cdr p)) (display ")")) ; devide by 2 (define (getcar n) (getcar-iter n 0)) (define (getcar-iter n a) (if (= (remainder n 2) 0) (getcar-iter (/ n 2) (+ a 1)) a)) ; devide by 3 (define (getcdr n) (getcdr-iter n 0)) (define (getcdr-iter n b) (if (= (remainder n 3) 0) (getcdr-iter (/ n 3) (+ b 1)) b)) (define (get-num n ) (cons (getcar n) (getcdr n))) (define p (get-num 9)) (print-point p) コメント 赤字が追加部分 remainderのサブルーチンは共通化できるが未実施 (0,2)
- 9. 問 2.6 ; n+1 (define (add1 n) (lambda (f) (lambda (x) (f ((n f) x))))) ;0 (define zero (lambda (f) (lambda (x) x))) ; 1= ramuda f x f x ;;;(print "cunning") ; from danboykis.com ;;;(add-1 zero) ;;;(add-1 (lambda (f) (lambda (x) x))) ;;;(lambda (f) (lambda (x) (f (((lambda (f) (lambda (x) x)) f) x)))) ;;;(lambda (f) (lambda (x) (f ((lambda (x) x) x)))) ;;;(lambda (f) (lambda (x) (f x))) (define one (lambda (f) (lambda (x) (f x )))) ;2 (define two (lambda (f) (lambda (x) (f(f x))))) ;3 (define three (lambda (f) (lambda (x) (f(f(f x))))))
- 10. 問 2.6 その2 ;m+n (define (addc m n) (lambda (f) (lambda (x) ((m f) ((n f) x))))) ;;;;;;; verification (define (inc n) (+ n 1)) (print ((zero inc) 0)) (print ((one inc) 0)) (print ((two inc) 0)) (print ((three inc) 0)) (print (((add1 zero) inc) 0)) (print (((add1 one) inc) 0)) (define (bai n) (* n 2)) (print ((one bai) 1)) (print ((two bai) 1)) (print ((three bai) 1)) ;;;;; Question ;;;;;;; (print "1+3=") (print (((addc one three) inc) 0)) ;(print (((addc2 one three) inc) 0)) (print (((addc one three) bai) 1)) ;;;;; Question ;;;;; (print (((addc three three) bai) 1)) ;;;;; Question ;;;;;