�ݺ�ߣ

Lesson 1:
Simplifying Expressions
Prepared by: Hannaniah S. Jimanga

Objectives:
At the end of this lesson, the learners are expected to:
1. Apply definitions, properties, axioms, theorems to
simplify algebraic expressions, equations and
inequalities.

Evaluate the following by applying the laws in
operations of integers and grouping symbols.
Show your step by step process.

The Properties of the Real Numbers
• Commutative Property
• Commutative Property of Addition
For any real number and ,
• Commutative Property of Multiplication
For any real number and ,

• Associative Property
• Associative Property of Addition
For any real number , ,
• Associative Property of Multiplication
For any real number ,

• Distributive Property
For any real number , ,

• Identity Properties
• Additive Identity Property
For any real number , .
• Multiplicative Identity Property
For any real number , .

• Inverse Properties
• Additive Inverse Property
For any real number , there is a unique number such that
.
Note: The sum of a number a and its additive inverse is zero
• Multiplicative Inverse Property
For any real number , there is a unique number such that
.
Note: The product of a number and its reciprocal is 1

Example: Simplify the following expressions using the properties of
real numbers.

Lesson 2
Linear and Quadratic Equations

Equations
• An equation is a sentence that expresses the equality of
two algebraic expressions.
• Given that , solve for the solution or root of the equation.

The expression has ___ terms.
____ are the variable terms and ___ is the constant
term.
In each variable term, ____ is the numerical
coefficient, and ___ is the variable part.
2 𝑥2
+5 𝑥 − 8

Identify if the given values satisfies the equation (makes
the equation true).
1. when , and
2. when , and
3. when , , and

Application
• The diameter of the base of a right circular cylinder is
5cm. The height of the cylinder is 8.5cm. Find the
volume of the cylinder. Round to the nearest tenth.

Properties of Equality
• Addition Property of Equality (APE)
Adding the same number to both sides of the equation does not
change the solution set to the equation. In symbols, if , then .
• Multiplication Property of Equality
Multiplying both sides of an equation by the same nonzero number
does not change the solution set to the equation. In symbols, if and ,
then .

Solving Equations
Solve for the solution of the given equations by applying the different
properties.

Linear Inequalities
A linear inequality in one variable is any inequality of the
form , when and are real numbers, with . In place of we may
also use .

Properties of Inequalities
• Addition Property of Inequality
If the same number is added to both sides of an inequality, then the
solution set to the inequality is unchanged.
• Multiplication Property of Equality
If both sides of an inequation are multiplied by the same positive
number, then the solution set to the inequality is unchanged.
If both sides of an inequation are multiplied by the same negative
number, and the inequality symbol is reversed, then the solution set to
the inequality is unchanged.

Quadratic Equations
Quadratic equations has the form , where , , and are real
numbers and .
Zero Factor Property
The equation is equivalent to the compound equation or .

Solving Quadratic Equations by
Factoring
Example:
Solve by factoring.

Completing the Square,
Rule for finding the Last Term
The last term of the a perfect square trinomial is the square
of one-half of the coefficient of the middle term. In symbols,
the perfect square whose first two terms are is

Example:
Solve the following by completing the square.

Example: Strategy:
• If , then divide each side by .
• Get only the and the terms on the left-
hand side.
• Add to each side the square of the
coefficient .
• Factor the left-hand side as the square
of binomial.
• Solve for .
• Simplify.

Quadratic Formula
Th solution of with , is given by the formula:

Number of solutions to a Quadratic Equation
The quadratic equation with has;
Two real solutions
One real solutions
No real solutions (two
imaginary solutions)
discriminant

Number of solutions to a Quadratic Equation
Example: Use the discriminant to identify the number of
real solutions and find the roots by using the quadratic
formula.

Quadratic Inequality
A quadratic inequality has one of the forms
Where , , and are real numbers with .

Lesson 3
Absolute Value Inequality

Absolute Value
The absolute value ofis a number whose distance from 0
on the number line is units.
Example:
Solution set:

Absolute Inequality
Basic Absolute Value Inequalities
Absolute value
inequality
Equivalent
Inequality
Solution set Graph of the
Solution Set
) (
-k k
] [
-k k
( )
-k k
[ ]
-k k

Absolute Value
Solve for
Solution: No real numbers. Since , we write inequalities
only when the value of is positive.

Lesson 4
Mathematical modelling

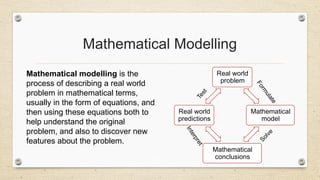
Mathematical Modelling
Mathematical modelling is the
process of describing a real world
problem in mathematical terms,
usually in the form of equations, and
then using these equations both to
help understand the original
problem, and also to discover new
features about the problem.
Real world
problem
Mathematical
model
Mathematical
conclusions
Real world
predictions
F
o
r
m
u
l
a
t
e
Solve
I
n
t
e
r
p
r
e
t
T
e
s
t

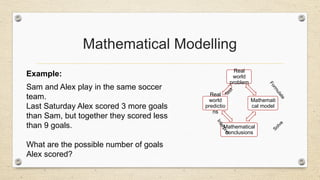
Example:
Sam and Alex play in the same soccer
team.
Last Saturday Alex scored 3 more goals
than Sam, but together they scored less
than 9 goals.
What are the possible number of goals
Alex scored?
Real
world
problem
Mathemati
cal model
Mathematical
conclusions
Real
world
predictio
ns
F
o
r
m
u
l
a
t
e
Solve
I
n
t
e
r
p
r
e
t
T
e
s
t

Example:
Regina makes $6.80 per hour in a café.
To keep her scholarship grant, she may
not earn more than $51 per week. What
is the range of the number of hours per
week that she may work?
Real
world
problem
Mathemati
cal model
Mathematical
conclusions
Real
world
predictio
ns
F
o
r
m
u
l
a
t
e
Solve
I
n
t
e
r
p
r
e
t
T
e
s
t

Example:
A boxing ring is in the shape of a square,
20ft on each sides. How far apart are the
fighters when they are in opposite
corners of the ring?
Real
world
problem
Mathemati
cal model
Mathematical
conclusions
Real
world
predictio
ns
F
o
r
m
u
l
a
t
e
Solve
I
n
t
e
r
p
r
e
t
T
e
s
t

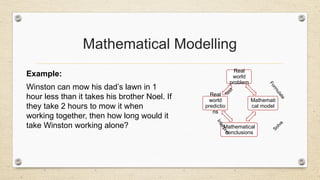
Example:
Winston can mow his dad’s lawn in 1
hour less than it takes his brother Noel. If
they take 2 hours to mow it when
working together, then how long would it
take Winston working alone?
Real
world
problem
Mathemati
cal model
Mathematical
conclusions
Real
world
predictio
ns
F
o
r
m
u
l
a
t
e
Solve
I
n
t
e
r
p
r
e
t
T
e
s
t

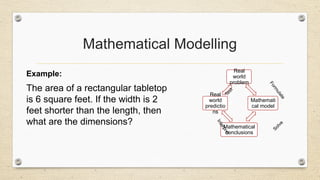
Example:
The area of a rectangular tabletop
is 6 square feet. If the width is 2
feet shorter than the length, then
what are the dimensions?
Real
world
problem
Mathemati
cal model
Mathematical
conclusions
Real
world
predictio
ns
F
o
r
m
u
l
a
t
e
Solve
I
n
t
e
r
p
r
e
t
T
e
s
t

simplifying expressions in algebra lesson 1

�ݺ�ߣ

simplifying expressions in algebra lesson 1

Recommended

More Related Content

Similar to simplifying expressions in algebra lesson 1 (20)

Recently uploaded (20)

simplifying expressions in algebra lesson 1

Editor's Notes