�ݺ�ߣ

T.C. İSTANBUL AYDIN ÜNİVERSİTESİ
-BİLGİSAYAR MÜHENDİSLİĞİ YÜKSEK LİSANS-BYL563İleri Algoritma Analizi-

BAZI SIRALAMA
ALGORİTMALARININ
KARŞILAŞTIRMALI
ANALİZİ

Hazırlayan:Veysi ERTEKİN(YL1213.010020)

İçindekiler
A.

Problemin Tanımı ...................................................................................................................................................... 3

B.

Sıralama Algortimaları............................................................................................................................................... 3
1.

Bouble sort: ........................................................................................................................................................... 3

2.

Insertion sort: ........................................................................................................................................................ 4

3.

Selection Sort: ....................................................................................................................................................... 4

4.

Merge Sort: ........................................................................................................................................................... 5

5.

Quick Sort: ............................................................................................................................................................. 6

6.

Heap Sort: ............................................................................................................................................................. 7

C.

Algoritmaların Analizi ................................................................................................................................................ 8

D.

Ekler ........................................................................................................................................................................ 10
1. TestCase.java:......................................................................................................................................................... 10
2.
3.

BubbleSort.java: .................................................................................................................................................. 11

4.

HeapSort.java: ..................................................................................................................................................... 11

5.

InsertionSort.java: ............................................................................................................................................... 12

6.

MergeSort.java:................................................................................................................................................... 12

7.

QuickSort.java: .................................................................................................................................................... 13

8.

SelectionSort.java: .............................................................................................................................................. 14

9.
E.

Main.java:............................................................................................................................................................ 11

AAlgorithm.java (Abstract Class):........................................................................................................................ 14
Kaynakça ................................................................................................................................................................. 15

A. Problemin Tanımı
Herhangi bir sayıdaki aynı tip verilerin sınırlı bellek ve işlem gücü ile belirli bir sıraya göre dizilmesinin
sağlanmasıdır. Burada önemli olan en optimum bellek/performans ikilisini verecek bir algoritma(yöntem)nın elde
edilmesidir.
Sıralama algoritmaları bazı kriterlere göre sınıflandırılabilir:
Hesaplama karmaşıklığı: oluşturulmuş olan algoritmanın yaptığı işlem sayısının genel bir yapı ile
ifade edilmesidir. Temel üç grup ölçek kullanılır. Bunlar en iyi(best), ortalama(average) ve en
kötü(worst) durum olarak belirtilir. Örnek verilecek olursa Big O belirteci algoritma karmaşıklığının
üst sınırını belirtmek adına oluşturulmuştur. İşlem yoğunluğu zamanın işleyişiyle paralel
olduğundan(ne kadar çok işlem yapılırsa o kadar uzun süre geçer) algoritmanın işleyiş süresini de
etkiler.
Yerdeğiştirmelerin Karmaşıklığı: içerisinde ek bellek kullanmayan(in place) algoritmalarda kullanılan
karşılaştırılabilmesi içinönemli bir ölçüttür.
Bellek Kullanımı: çalışırken ek bellek ihtiyacı duyan algoritmalarda kullanılabilecek bir ölçüttür.
Rekürsiflik: iç içe kendi kendini çağıran algoritmalarda kullanılan bir ölçüttür. Burada en önemli kriter
stack dediğimiz maximum iç içe çağrım kapasitesine dikkat edilmesi ve bu kapasitenin kullanılma
sıklığıdır.
Durağanlık(stability): algoritmanın uygulanması sırasında sıralanmış bir verinin tekrar sıralamaya
tabi tutulup tutulmadığını belirten ölçüttür.

B. Sıralama Algortimaları
1. Bouble sort:
“Kabarcık sıralaması”nda sırasıyla ikililer şeklinde karşılaştırma yapılır, belirlenen sıralama ölçütüne bağlı
olarak verilerin hangisinin önde veya arkada olacağının bulunması ve eğer verilerin yanlış bir sırada olmasının
tespit edilmesi durumunda yerlerinin birbiriyle değiştirilmesine (swapping) dayanır.
En iyi
n.log(n)

Ortalama
n.log(n)

En kötü
n^2

(Genel algoritma yapısı)
functionboubleSort(A:listofitems)
for(i=1;i<A.lenght-1;i++)
for(j=A.lenght;j>i;j--)
ifA[j]<A[j-1]
swap(j,j-1,A)// A[j] ile A[j-1]’in yerlerini değiştir.

Bellek
log(n)~n

Stabil mi?
Evet

2. Insertion sort:
Her bir değerin sırayla alınıp kendinden küçük ve kendinden büyük değerlerin arasına alınmasıyla
gerçekleştirilir.
En iyi
n

Ortalama
n^2

En kötü
n^2

Bellek
1

Stabil mi?
Evet

functioninsertionSort(a:listofitems)
for(i=1;i<a.lenght;i++)// her bir elemanı en az bir kere işle
inttemp=a[i];// seçilen elemanı tamponla
intj;
for(j=i-1;j>=0&&temp<a[j];j--)// en büyükten başlayarak kendinden büyükleri bir
öne al
a[j+1]=a[j]
a[j+1]=temp;// en son öne aldığımızın bir altına o anki elemanı koy

3. Selection Sort:
İlk olarak elimizdeki bütün elemanlardan en küçük olanı bulunur ve ilk sıraya konur. İkinci olarak geriye
kalanların en küçüğü bulunur ve ikinci sıraya konur. Bu şekilde elimizde bir eleman kalana kadar küçük elemanlar
bulunarak dizilirler.
En iyi
n^2

Ortalama
n^2

En kötü
n^2

functionselectionSort(a:listofitems)
inti,j;
intmin;
for(j=0;j<n-1;j++)
min=j;
for(i=j+1;i<n;i++)
if(a[i]<a[min])
min=i;
if(min !=j)// Eğer en küçük sayı bulunmuşsasıraya ekle
swap(a[j],a[min]);

Bellek
1

Stabil mi?
Hayır

4. Merge Sort:
Elimizdeki veri dizisinin logaritmik olarak yarı yarıya bölünüp sonrasında ikişerli gruplar halinde sıralanarak
birleştirilmesi ardındanda birleştirilen grupların kendi aralarında bütün gruplar birleşene kadar seviye seviye
sıralanarak birleştirilmesinden oluşur.

En iyi
n.log(n)

Ortalama
n.log(n)

En kötü
n.log(n)

Bellek
n

Stabil mi?
Evet

functionmerge_sort(listm)// bu kısım elimizdeki liste parçasını önce bülüp sonrasında
//

sonrasında bölünmüş parçaları “merge” methodu ile
// sıralanarak birleştirilmesini sağlıyor.

iflength(m)<=1
returnm
varlistleft,right
varintegermiddle=length(m)/2
foreachxinmbeforemiddle
addxtoleft
foreachxinmafterorequalmiddle
addxtoright
left=merge_sort(left)
right=merge_sort(right)
returnmerge(left,right)
functionmerge(left,right)
varlistresult
whilelength(left)>0orlength(right)>0
iflength(left)>0andlength(right)>0
iffirst(left)<=first(right)
appendfirst(left)toresult
left=rest(left)
else
appendfirst(right)toresult
right=rest(right)
elseiflength(left)>0
appendfirst(left)toresult
left=rest(left)
elseiflength(right)>0
appendfirst(right)toresult
right=rest(right)
endwhile
returnresult

5. Quick Sort:
Şu ana kadar bilinen en gözde ve hızlı algoritmadır. Uygulama adımları şu şekilde sıralanabilir:
Diziden herhangi bir eleman al(pivot eleman).
Pivot elemanından küçük olanları bir diziye, büyükleri bir diziye topla.
Bu alt dizilerden yukarıdaki gibi pivot elemanlar seçip aynı işlemi uygula. İç içe en küçük parçalara
ulaşana kadar bu yöntemi sürdür.
Oluşan dizicikleri birleştir.

En iyi
n.log(n)

Ortalama
n.log(n)

En kötü
n^2

functionquicksort(intlow,inthigh,listnumbers)
inti=low,j=high;
intpivot=numbers[low+(high-low)/2];
while(i<=j)
while(numbers[i]<pivot)
i++;
while(numbers[j]>pivot)
j--;
if(i<=j)
swap(i,j,numbers);
i++;
j--;
if(low<j)
quicksort(low,j);
if(i<high)
quicksort(i,high);
functionswap(inti,intj,listnumbers) // yerlerini değiştir
inttemp=numbers[i];
numbers[i]=numbers[j];
numbers[j]=temp;

Bellek
log(n)~n

Stabil mi?
Evet

6. Heap Sort:
Verilerden bir heap tree oluşturulur. Sonrasında sırayla kökteki elemanlar çekilir. Böylece datamız sıralanmış
olunur.
En iyi
n.log(n)

Ortalama
n.log(n)

privateInteger[]array;
privateintlargest;
privateintsol;
privateintn;
privateintsag;
functionheapSort(Integer[]array)
this.array=array;
heapOlustur();
for(inti=n;i>0;i--)
swap(0,i);
n=n-1;
enBuyuk(0);
returnarray;
functionheapOlustur()
n=array.length-1;
for(inti=n/2;i>=0;i--)
enBuyuk(i);
functionswap(inti,intj)
intt=array[i];
array[i]=array[j];
array[j]=t;
functionenBuyuk(inti)
sol=2*i;
sag=2*i+1;
if(sol<=n&&array[sol]>array[i])
largest=sol;
else
largest=i;
if(sag<=n&&array[sag]>array[largest])
largest=sag;
if(largest !=i)
swap(i,largest);
enBuyuk(largest);

En kötü
n.log(n)

Bellek
1

Stabil mi?
Hayır

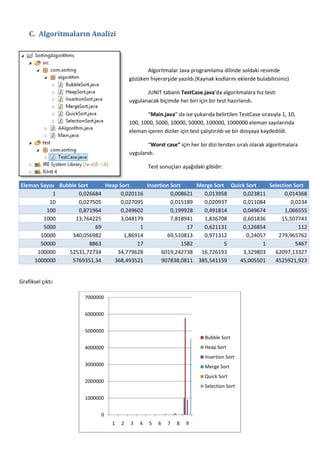
C. Algoritmaların Analizi

Algoritmalar Java programlama dilinde soldaki resimde
gözüken hiyerarşide yazıldı.(Kaynak kodlarını eklerde bulabilirsiniz)
JUNIT tabanlı TestCase.java’da algoritmalara hız testi
uygulanacak biçimde her biri için bir test hazırlandı.
“Main.java” da ise yukarıda belirtilen TestCase sırasıyla 1, 10,
100, 1000, 5000, 10000, 50000, 100000, 1000000 eleman sayılarında
eleman içeren diziler için test çalıştırıldı ve bir dosyaya kaydedildi.
“Worst case” için her bir dizi tersten sıralı olarak algoritmalara
uygulandı.
Test sonuçları aşağıdaki gibidir:
Eleman Sayısı Bubble Sort
Heap Sort
Insertion Sort
Merge Sort Quick Sort
Selection Sort
1
0,026684
0,020116
0,008621
0,013958
0,023811
0,014368
10
0,027505
0,027095
0,015189
0,020937
0,011084
0,0234
100
0,871964
0,249602
0,199928
0,491814
0,049674
1,066555
1000
13,764225
3,048179
7,818941
1,836708
0,601836
15,507743
5000
69
1
17
0,621131
0,126854
112
10000
340,056982
1,86914
69,510813
0,971312
0,24057
279,965762
50000
8863
17
1582
5
1
5467
100000
52531,72734
34,779628
6019,242738 16,726193
3,329803
62097,13327
1000000
5769351,34
368,493521
907838,0811 385,541159
45,005501
4525921,923

Grafiksel çıktı:
7000000
6000000
5000000
Bubble Sort
Heap Sort

4000000

Insertion Sort
3000000

Merge Sort
Quick Sort

2000000

Selection Sort

1000000
0
1

2

3

4

5

6

7

8

9

Yatay grafiksel çıktı:

6000000
5000000

Bubble Sort

4000000

Heap Sort

3000000

Insertion Sort
Merge Sort

2000000

Quick Sort
1000000

Selection Sort
Merge Sort

0
1

2

3

4

5

Bubble Sort
6

7

8

9

Sonuç:Grafiklerden de anlaşılacağı üzere yüksek elemanlı dizilerde hız açısından en hızlıdan en yavaşa olan sıralama
aşağıdaki gibi tespit edilmiştir.

Quick Sort, Merge Sort, Heap Sort, Insertion Sort, Selection Sort,Bouble Sort

D. Ekler
1. TestCase.java:
package com.sorting;
import java.util.HashMap;
import java.util.Map;
import
import
import
import
import

org.junit.After;
org.junit.Before;
org.junit.Rule;
org.junit.Test;
org.junit.rules.TestName;

publicclass TestCase {
AAlgorithm algorithm;
@Rule
public TestName name =new TestName();
Integer[] numbers;
publicstaticint SIZE =0;
publicstatic Map<String, Double> map =new HashMap<String, Double>();
long start;
@Before
publicvoid setUp()throws Exception {
algorithm = createObject(Class.forName("com.sorting.algorithm."+ name.getMethodName()));
numbers = generateArray(SIZE);
start = System.nanoTime();
}
@After
publicvoid tearDown()throws Exception {
double duration =(System.nanoTime()- start)/1000000D;
map.put(name.getMethodName(), duration);
}
@Test
publicvoid BubbleSort(){
algorithm.sort(numbers);
}
@Test
publicvoid HeapSort(){
}
@Test
publicvoid InsertionSort(){
}
@Test
publicvoid MergeSort(){
}
@Test
publicvoid QuickSort(){
}
@Test
publicvoid SelectionSort(){
}
@SuppressWarnings("rawtypes")
publicstatic AAlgorithm createObject(Class klass){
try{
return(AAlgorithm) klass.newInstance();
}
catch(Exception e){
e.printStackTrace();
returnnull;
}
}
publicstatic Integer[] generateArray(Integer size){
Integer[] array =new Integer[size];

for(int i = size -1, j =0; i >=0; i--, j++){
array[j]= i;
}
return array;
}
}

2. Main.java:
import java.io.File;
import java.io.FileNotFoundException;
import java.io.PrintWriter;
import org.junit.runner.JUnitCore;
publicclass Main {
publicstaticvoid main(String[] args)throws FileNotFoundException {
PrintWriter print =new PrintWriter(System.getProperty("user.home")+ File.separator +"Desktop"+
File.separator +"x.csv");
TestCase.SIZE =1;
String line ="";
int repeat =7;
for(int i =0; i < repeat; i++){
JUnitCore.runClasses(TestCase.class);
print.print(line + TestCase.SIZE +"t"+ TestCase.map.get("BubbleSort")+"t"+
TestCase.map.get("HeapSort")+"t"+ TestCase.map.get("InsertionSort")+"t"
+ TestCase.map.get("MergeSort")+"t"+ TestCase.map.get("QuickSort")+"t"+
TestCase.map.get("SelectionSort"));
line ="n";
TestCase.map.clear();
TestCase.SIZE *=10;
}
print.close();
System.out.println();
}
}

3. BubbleSort.java:
package com.sorting.algorithm;
import com.sorting.AAlgorithm;
publicclass BubbleSort extends AAlgorithm {
@Override
public Integer[] sort(Integer[] array){
int length = array.length;
for(int i =0; i < length; i++){
for(int j = length -1; j > i; j--){
if(array[j]< array[j -1]){
swap(j, j -1, array);
}
}
}
return array;
}
}

4. HeapSort.java:
publicclass HeapSort extends AAlgorithm {
private Integer[] array;
privateint largest;
privateint left;
privateint n;
privateint right;
publicvoid buildheap(){
n = array.length -1;
for(int i = n /2; i >=0; i--){
maxheap(i);

}
}
publicvoid exchange(int i,int j){
int t = array[i];
array[i]= array[j];
array[j]= t;
}
publicvoid maxheap(int i){
left =2* i;
right =2* i +1;
if(left <= n && array[left]> array[i]){
largest = left;
}
else{
largest = i;
}
if(right <= n && array[right]> array[largest]){
largest = right;
}
if(largest != i){
exchange(i, largest);
maxheap(largest);
}
}
@Override
this.array = array;
buildheap();
for(int i = n; i >0; i--){
exchange(0, i);
n = n -1;
maxheap(0);
}
return array;
}
}

5. InsertionSort.java:
publicclass InsertionSort extends AAlgorithm {
@Override
for(int i =1; i < array.length; i++){
int temp = array[i];
int j;
for(j = i -1; j >=0&& temp < array[j]; j--){
array[j +1]= array[j];
}
array[j +1]= temp;
}
return array;
}
}

6. MergeSort.java:
publicclass MergeSort extends AAlgorithm {
private Integer[] numbers;
privateint[] helper;
privateint number;
@Override
public Integer[] sort(Integer[] values){
this.numbers = values;
number = values.length;

this.helper =newint[number];
mergesort(0, number -1);
return values;
}
privatevoid mergesort(int low,int high){
if(low < high){
int middle = low +(high - low)/2;
mergesort(low, middle);
mergesort(middle +1, high);
merge(low, middle, high);
}
}
privatevoid merge(int low,int middle,int high){
for(int i = low; i <= high; i++){
helper[i]= numbers[i];
}
int i = low;
int j = middle +1;
int k = low;
while(i <= middle && j <= high){
if(helper[i]<= helper[j]){
numbers[k]= helper[i];
i++;
}
else{
numbers[k]= helper[j];
j++;
}
k++;
}
while(i <= middle){
numbers[k]= helper[i];
k++;
i++;
}
}
}

7. QuickSort.java:
publicclass QuickSort extends AAlgorithm {
private Integer[] numbers;
private Integer number;
@Override
public Integer[] sort(Integer[] values){
if(values ==null|| values.length ==0){
return values;
}
this.numbers = values;
number = values.length;
quicksort(0, number -1);
return values;
}
privatevoid quicksort(int low,int high){
int i = low, j = high;
int pivot = numbers[low +(high - low)/2];
while(i <= j){
while(numbers[i]< pivot){
i++;
}
while(numbers[j]> pivot){
j--;
}
if(i <= j){
swap(i, j, numbers);
i++;
j--;
}
}
if(low < j)
quicksort(low, j);
if(i < high)
quicksort(i, high);
}
}

8. SelectionSort.java:
publicclass SelectionSort extends AAlgorithm {
@Override
Integer i, j;
Integer min;
Integer n = array.length;
for(j =0; j < n -1; j++){
min = j;
for(i = j +1; i < n; i++){
if(array[i]< array[min]){
min = i;
}
}
if(min != j){
swap(j, min, array);
}
}
return array;
}
}

9. AAlgorithm.java (Abstract Class):
publicabstractclass AAlgorithm {
publicabstract Integer[] sort(Integer[] array);
public Integer[] swap(int i,int j, Integer[] array){
int temp = array[i];
array[i]= array[j];
array[j]= temp;
return array;
}
}

E. Kaynakça
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.

http://en.wikipedia.org/wiki/Sorting_algorithm
http://www.vogella.com/articles/JavaAlgorithmsQuicksort/article.html
http://www.vogella.com/articles/JavaAlgorithmsMergesort/article.html
http://en.wikipedia.org/wiki/Bubble_sort
http://www.cprogramming.com/tutorial/computersciencetheory/sorting1.html
http://www.youtube.com/watch?v=EeQ8pwjQxTM
http://en.wikipedia.org/wiki/Merge_sort
http://en.wikipedia.org/wiki/Quicksort
http://www.cs.auckland.ac.nz/~jmor159/PLDS210/qsort.html
http://www.sorting-algorithms.com/quick-sort
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/quickSort.htm
http://algs4.cs.princeton.edu/23quicksort/
http://en.wikipedia.org/wiki/Heapsort
http://www.youtube.com/watch?v=6NB0GHY11Iw

�ݺ�ߣ

Siralama algoritmalari ileri algoritma analizi

More Related Content

Siralama algoritmalari ileri algoritma analizi