Sistem persamaan linear (spl)
- 1. P E R T E M U A N K E - 3 U M M U S A L A M A H Sistem Persamaan Linear (SPL) dan Kuadrat (SPK)
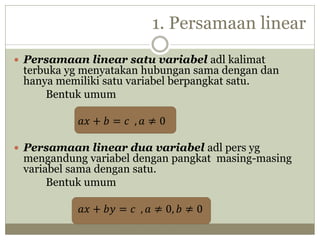
- 2. 1. Persamaan linear Persamaan linear satu variabel adl kalimat terbuka yg menyatakan hubungan sama dengan dan hanya memiliki satu variabel berpangkat satu. Bentuk umum + = , 0 Persamaan linear dua variabel adl pers yg mengandung variabel dengan pangkat masing-masing variabel sama dengan satu. Bentuk umum + = , 0, 0
- 3. 2. Sistem Pers. Linear Dua Variabel (SPLDV) SPLDV adl sistem pers yg mengandung paling sedikit sepasang (dua buah) pers linear dua variabel yg hanya mempunyai satu penyelesaian. Bentuk umum 1 + 1 = 1 2 + 2 = 2 1, 1, 1, 2, 2 dan 2
- 4. Lanjutan 2 Contoh Jika dan memenuhi sistem persamaan 2 + = 5 3 2 = 3 tentukan nilai , dan + y , serta sketsakan grafiknya. Latihan Himpunan penyelesaian sistem persamaan linear 7 + 5 = 2 5 + 7 = 2 adalah {x, y}. Tentukan nilai , serta sketsakan grafiknya.
- 5. Lanjutan 2 Contoh Soal cerita Sepuluh tahun yg lalu umur Aldy dua kali umur Bony, lima tahun yg kemudian umur Aldy 1 1 2 kali umur Bony. Sekarang umur Aldy dan Bony adl Latihan Soal Cerita Dua kali umur Amira ditambah tiga kali umur Yulia adl 61 tahun, sedangkan empat kali umur Yulia dikurangi tiga kali umur Amira adl 19 tahun, umur Amira dijumlahkan dgn umur Yulia adl
- 6. 3. Sistem Pers. Linear Tiga Variabel (SPLTV) Bentuk umum 1 + 1 + 1 = 1 2 + 2 + 2 = 2 3 + 3 + 3 = 3 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, dan3
- 7. Lanjutan 3 Contoh : Himpunan penyelesaian dari sistem persamaan + 2 = 5 2 + = 9 2 + 3 = 4 adalah Latihan 1 Himpunan penyelesaian dari sistem persamaan 2 + 4 6 = 16 3 3 + 2 = 6 4 + 3 = 22 adalah {x, y, z} maka nilai x : y : z =
- 8. Latihan 2 Jika , dan adalah penyelesaian dari sistem persamaan 3 + 2 = 7 4 3 2 + 2 = 6 6 4 3 = 1 maka nilai = .
- 9. 4. Sistem Pers. Linear dan Kuadrat Dua Variabel (SPLKDV) Bentuk umum SPLKDV dengan variabel dan adalah = + (＄ ) = 2 + + (＄ ) dengan , , , ,
- 10. Lanjutan 4 Contoh Himpunan penyelesaian dari sistem persamaan = 3 = 2 4 + 3 adalah Latihan Himpunan penyelesaian sistem persamaan = 7 = 2 + 3 10 adalah {(1, 1); (2, 2)}, maka nilai 1 2
- 11. 5. Sistem Persamaan Kuadrat (SPK) Bentuk umum SPK dengan variabel dan adalah = 2 + + = 2 + + dengan , , , , ,
- 12. Lanjutan 5 Contoh Himpunan penyelesaian dari sistem persamaan = 2 2 3 = 2 2 + 5 adalah Latihan Jika dan adalah penyelesaian dari sistem persamaan = 2 + 7 + 12 = 2 5 + 22 maka nilai 1 + 2 = .
- 13. Program Linear Sistem Pertidaksamaan Linear Pertidaksamaan linear adalah pertidaksamaan dg pangkat tertinggi dari variabelnya satu, gabungan dua atau lebih pertidaksamaan linear disebut sistem pertidaksamaan linear. Lambang yg digunakan (<, , >, ) Himpunan penyelesaian pertidaksamaan dapat ditentukan dengan menggunakan metode grafik dan uji titik. Tanpa melakukan uji titik, daerah himpunan penyelesaian suatu pertidaksamaan linear dapat ditentukan dengan aturan sbb.
- 14. Pertidaksamaan > < + Daerah himpunan penyelesaian berada di kanan/di atas garis + = Daerah himpunan penyelesaian berada di kiri/di bawah garis + = + Daerah himpunan penyelesaian berada di kiri/di bawah garis + = Daerah himpunan penyelesaian berada di kanan/di atas garis + =
- 15. Contoh 1 Himpunan penyelesaian sistem pertidaksamaan 2 + 40 + 2 40 0 0 Terletak pada daerah yang berbentuk .
- 16. Contoh 2 Perhatikan gambar (papan tulis) Daerah yang diarsir pada gambar menunjukkan himpunan penyelesaian dari pembatasan-pembatasan untuk bilangan-bilangan real dan . Tentukan pembatasan-pembatasan atau pertidaksamaannya!
- 17. Latihan 1. Himpunan penyelesaian pertidaksamaan 2 + 4 ; 3 + 4 12 ; 0 ; 0 Dapat digambarkan dengan bagian bidang yang diarsir, yaitu 2. Daerah yang diarsir pada gambar (papan tulis) di samping merupakan himpunan penyelesaian sistem pertidaksamaan
- 18. Program Linear dan Model Matematika Program linear adalah satu bagian dari matematika terapan yang digunakan untuk memecahkan masalah pengoptimalkan (memaksimalkan atau meminimalkan suatu tujuan, seperti mencari keuntungan maksimum dari penjualan suatu produk. Dalam memecahkan masalah pengoptimalkan dgn program linear, terdapat kendala-kendala atau batasan- batasan yang harus diterjemahkan ke dalam suatu pertidaksamaan linear yang disebut pemodelan matematika, dan sistem pertidaksamaan linear yang terbentuk disebut model matematika.
- 19. Contoh Untuk membuat barang A diperlukan 6 jam pada mesin I dan 4 jam pada mesin II, sedangkan membuat barang jenis B memerlukan 2 jam pada mesin I dan 8 jam pada mesin II. Kedua mesin tersebut setiap harinya masing-masing bekerja tidak lebih dari 18 jam. Jika setiap hari dibuat x buah barang A dan y buah barang B, maka model matematika dari uraian tersebut adalah
- 20. Latihan Sebuah pesawat udara mempunyai tempat duduk tidak lebih dari 48 penumpang. Setiap penumpang kelas utama boleh membawa bagasi 60 kg sedangkan untuk kelas ekonomi 20 kg. Pesawat ini hanya dapat membawa bagasi 1440kg, bila dan berturut-turut menyatakan banyak penumpang kelas utama dan ekonomi, maka model matematika dan persoalan di atas adalah .
- 21. Nilai Optimum Suatu Bentuk Objektif Dalam program linear, bentuk objektif atau fungsi objektif adalah bentuk atau fungsi , = + yg hendak dioptimumkan (dimaksimumkan atau diminimumkan) Nilai optimum bentuk objektif dapat ditentukan dengan garis selidik atau metode titik pojok (titik sudut)
- 22. Contoh Tanah seluas 10.000 m2 akan dibangun rumah tipe M dan tipe N. untuk rumah tipe M diperlukan 100 m2 dan tipe N diperlukan 75 m2. jumlah rumah yang dibangun paling banyak 125 unit. Keuntungan rumah tipe M adalah Rp 6.000.000,- /unit dan tipe N adalah Rp 4.000.000,-/unit. Keuntungan maksimum yang dapat diperoleh dari penjualan rumah tersebut adalah
- 23. Latihan Luas daerah parkir 1760 m2, luas rata-rata untuk mobil sedan 4 m2 dan bus 20 m2. daya muat maksimum hanya 200 kendaraan, biaya parkir untuk mobil sedan Rp 2000,- dan untuk bus Rp 5000,-. Tentukan hasil maksimum dari tempat parkir tsb adalah