Sns mid term-test2-solution
1 like704 views
This document contains a mid-term test for a signals and systems engineering diploma assessment. The test contains 4 questions that assess topics such as determining if signals are periodic or aperiodic, sketching signals, evaluating convolution sums and integrals, defining Laplace and z-transforms, and using properties like shifting to find impulse responses of linear time-invariant systems. The test aims to evaluate students' understanding of fundamental concepts in signals and systems.
1 of 8
Downloaded 14 times
![PSDC ENGINEERING DIPLOMA ASSESSMENT
Signals And Systems ¨C Mid-Term Test 2 (B16 CE/B17 EEA&EEB)
7th January 2009, Wednesday 2:00pm ¨C 5:00pm (3 hours)
Question 1 (Signals and Systems)
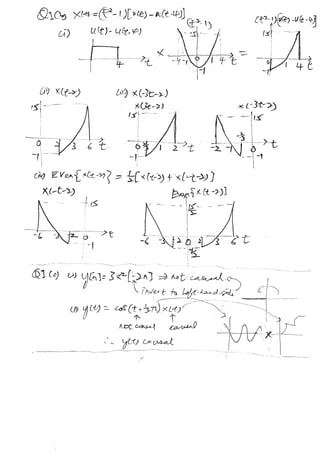
(a) Determine whether the following signals are periodic or aperiodic.
If it is a periodic signal, determine its power.
(i) x[n] = 2cos(?¦Đn) + sin(?¦Đn)
(ii) x(t) = Odd{cos(2¦Đt)}
(b) If x(t) = (t2 ¨C 1) [u(t) ¨C u(t¨C4)],
(i) Sketch x(t)
(ii) Sketch x(t ¨C 2)
(iii) Sketch x(¨C3t ¨C 2)
(iv) Sketch Even{x(t ¨C 2)}
(c) Determine the following systems are casual, linear and time-invariant.
(i) y[n] = 3x2[¨C2n]
(ii) y(t) = cos (t+ ? ¦Đ) x(t)
Question 2 (Convolution)
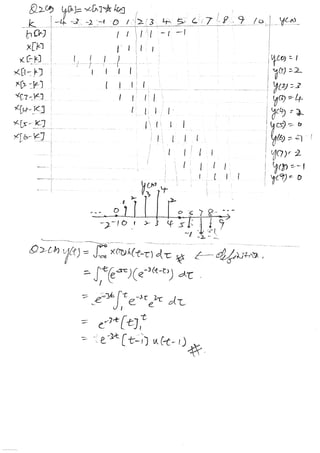
(a) Evaluate the convolution sum for y[n] = x[n]?h[n], where x[n] and h[n] are
shown in Fig. Q2 (a).
Fig. Q2 (a)
(b) Define the convolution of two signals x(t) and h(t).
Then, compute the convolution integral for y(t) = x(t)?h(t) of the following
signals:
h(t) = e¨C3tu(t) and x(t) = e¨C3tu(t¨C1).
1](https://image.slidesharecdn.com/snsmid-term-test2solution-110406043236-phpapp01/85/Sns-mid-term-test2-solution-1-320.jpg)
![PSDC ENGINEERING DIPLOMA ASSESSMENT
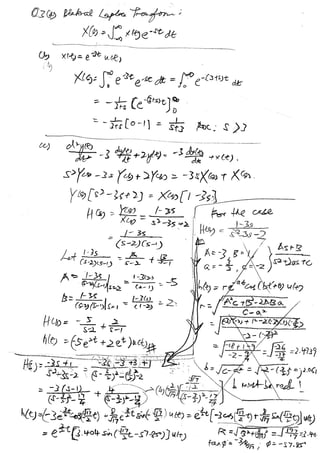
Question 3 (Laplace Transform)
(a) Define Bilateral (two-sided) Laplace Transform.
(b) Consider the signal, x(t) = e¨C3tu(t). Find the Laplace transform of x(t) with
the associated region of convergence (ROC).
(c) Consider a continuous-time LTI system described by
d 2 y( t ) dy( t ) dx( t )
2
?3 ? 2 y( t ) = ?3 + x( t )
dt dt dt
Using the shifting property, find the unit impulse response h(t).
Question 4 (z-Transform)
(a) Define Bilateral (two-sided) z-Transform.
(b) Consider the signal, x[k] = aku[k]. Find the z-transform of x[k] with the
associated region of convergence (ROC).
(c) Consider a discrete-time LTI system described by
y[k] ¨C y[k¨C1] ¨C 2 y[k¨C2] = x[k] + 2 x[k¨C1] + 2 x[k¨C2]
Using the shifting property, find the unit impulse response h[k].
"Learning without thought is useless; thought without learning is dangerous."
ѧ¶ř˛»ËĽÔňŘč,ËĽ¶ř˛»Ń§Ôň´ů.
2](https://image.slidesharecdn.com/snsmid-term-test2solution-110406043236-phpapp01/85/Sns-mid-term-test2-solution-2-320.jpg)



Recommended
Vektor dan Medan Vektor



Vektor dan Medan VektorKelinci Coklat
?
1. Dokumen membahas tentang vektor, termasuk definisi vektor, operasi vektor seperti jumlah vektor dan perkalian vektor dengan skalar, norma vektor, hasil kali titik dan silang dua vektor, proyeksi vektor, divergensi dan curl medan vektor, serta gradien medan skalar.
2. Berisi contoh soal dan penyelesaian tentang operasi vektor seperti hasil kali titik dua vektor, proyeksi vektDielektrik jaringan



Dielektrik jaringanSiti Julaiha
?
Dokumen tersebut membahas tentang sifat dielektrik jaringan tubuh manusia yang meliputi resistansi, kapasitansi, dan permitivitas. Jaringan biologi memiliki nilai konduktivitas dan permitivitas yang bervariasi tergantung frekuensi medan listrik yang diaplikasikan. Perbedaan sifat dielektrik antara jaringan sehat dan kanker disebabkan oleh perubahan komposisi mineral dan potensial membran sel.Pertidaksamaan Nilai Mutlak, Irasional, dan Pecahan



Pertidaksamaan Nilai Mutlak, Irasional, dan Pecahannova147
?
Pertidaksamaan Nilai Mutlak, Irasional, dan PecahanParametric Equations



Parametric EquationsDiponegoro University
?
Dokumen tersebut membahas tentang persamaan parametrik, termasuk definisi, kurva parametrik, turunan pertama dan kedua, luas area dan panjang busur, serta contoh-contoh soal.Calculus of variations



Calculus of variationsSolo Hermelin
?
Describes the mathematics of the Calculus of Variations.
For comments please contact me at solo.hermelin@gmail.com.
For more presentations on different subjects visit my website on http://www.solohermelin.comKalkulus 2



Kalkulus 2Emon Tobat
?
Dokumen tersebut membahas materi integral kalkulus mulai dari pengertian integral, rumus-rumus dasar integral, metode integrasi seperti substitusi dan integral parsial, serta penerapan integral untuk menghitung luas dan volume benda dua dan tiga dimensi.Tugas kalkulus 2 r



Tugas kalkulus 2 rAl Munawwaroh
?
1. Tugas kalkulus 2 membahas konsep-konsep dasar kalkulus seperti turunan, integral, nilai ekstrem, dan aplikasi turunan.
2. Dibahas pula sifat-sifat turunan, turunan fungsi trigonometri, persamaan garis singgung, jenis-jenis nilai stasioner, kecekungan fungsi, dan cara menggambar grafik fungsi.
3. Bagian akhir membahas aplikasi turunan seperti laju perubahanChapter 9 computation of the dft



Chapter 9 computation of the dftmikeproud
?
This document discusses efficient algorithms for computing the discrete Fourier transform (DFT), specifically the fast Fourier transform (FFT). It covers several FFT algorithms including decimation-in-time, decimation-in-frequency, and the Goertzel algorithm. The decimation-in-time algorithm recursively breaks down the DFT computation into smaller DFTs by decomposing the input sequence. This allows the computation to be performed in O(NlogN) time rather than O(N^2) time for a direct DFT computation. The document also discusses optimizations like in-place computation to reduce memory usage.

boylestad_introduccion_al_analisis_de_circuitos.pdfHederth Ayala Gamarra
?
Este documento introduce el concepto de resistencia el¨¦ctrica. Explica que la resistencia depende de cuatro factores: el material, la longitud, el ¨˘rea de secci¨®n transversal y la temperatura. Define la resistividad como una propiedad del material que determina su resistencia. Presenta una ecuaci¨®n para calcular la resistencia de alambres circulares en funci¨®n de estos factores.linear transfermation.pptx



linear transfermation.pptxUmme habiba
?
This document provides an introduction to linear transformations. It defines a linear transformation as a function that maps one vector space to another while preserving vector addition and scalar multiplication. Key concepts discussed include the domain, co-domain, range, and pre-image of a linear transformation. Examples are given to demonstrate linear transformations and functions that are not linear transformations. The relationship between linear transformations and matrices is also explained.Bahan ajar alin 2 rev 2014 pdf



Bahan ajar alin 2 rev 2014 pdfPawit Ngafani
?
Dokumen tersebut memberikan penjelasan tentang ruang vektor umum, ruang bagian, dan beberapa contohnya. Ruang vektor didefinisikan sebagai himpunan dengan operasi penjumlahan vektor dan perkalian skalar yang memenuhi 10 sifat tertentu. Ruang bagian adalah ruang vektor yang merupakan bagian dari ruang vektor lain dengan operasi yang sama.Koefisien binomial



Koefisien binomialoilandgas24
?
Dokumen tersebut membahas tentang koefisien binomial yang merupakan bilangan yang muncul dari hasil penjabaran ekspresi pemangkatan dua variabel seperti (a + b)n. Dokumen tersebut menjelaskan bahwa koefisien binomial dapat ditentukan menggunakan rumus kombinasi dan dibuktikan menggunakan teorema binomial.Second order homogeneous linear differential equations 



Second order homogeneous linear differential equations Viraj Patel
?
1) The document discusses second order linear homogeneous differential equations, which have the general form P(x)y'' + Q(x)y' + R(x)y = 0.
2) It describes methods for finding the general solution including reduction of order, and discusses the solutions when the coefficients are constants.
3) The general solution depends on the nature of the roots of the auxiliary equation: distinct real roots, repeated real roots, or complex roots.Medan vektor



Medan vektorEthelbert Phanias
?
1. Dokumen tersebut membahas konsep-konsep dasar vektor dan operator-operator vektor yang digunakan dalam medan dan gelombang elektromagnetik, seperti gradien, divergensi, dan curl.
2. Dibahas pula sistem koordinat kartesian, silindris, dan bola yang digunakan untuk merepresentasikan vektor dalam ruang tiga dimensi.
3. Operator-operator vektor digunakan untuk menghitung laju perubahan medan skalar dan vektor.Unit-1 Classification of Signals



Unit-1 Classification of SignalsDr.SHANTHI K.G
?
Classification of signals
Deterministic and Random signals
Continuous time and discrete time signal
Even (symmetric) and Odd (Anti-symmetric) signal
Periodic and Aperiodic signal
Energy and Power signal
Causal and Non-causal signal
Power Point Sistem Persamaan Linear Tiga Variabel



Power Point Sistem Persamaan Linear Tiga Variabelrestu sri rahayu
?
Sistem Persamaan Linear Tiga VariabelContoh soal fisika kuantum



Contoh soal fisika kuantumramainoei
?
1. Persamaan Laplacian dalam koordinat sferis dituliskan. Operator Hamiltonian untuk gerak elektron dalam medan listrik dan magnet juga ditulis.
2. Fungsi gelombang radial untuk atom ditulis dan dinormalisasi. Energi elektron untuk fungsi gelombang tersebut dicari.
3. Spinor untuk elektron dalam medan magnet ditulis. Periode getaran spinor tersebut dicari.
4. Persamaan Schwarz dibuktikan.
5. Nilai eigen dan fungsi eigen tSs 2013 midterm



Ss 2013 midtermDharmendra Dixit
?
The document is a mid-semester exam for a signals, systems and controls course. It contains 6 multi-part questions testing various concepts related to continuous-time and discrete-time linear time-invariant systems including impulse responses, step responses, Fourier series, Fourier transforms, and frequency responses. Students are instructed to show all work and write clearly without marking on the exam paper.Ss 2013 midterm



Ss 2013 midtermDharmendra Dixit
?
The document is a mid-semester exam for a signals, systems and controls course. It contains 6 multi-part questions testing various concepts related to continuous-time and discrete-time linear time-invariant systems including impulse responses, step responses, Fourier series, Fourier transforms, and frequency responses. Students are instructed to show all work and can use an open book with the signals and systems textbook.More Related Content
What's hot (20)
Chapter 9 computation of the dft



Chapter 9 computation of the dftmikeproud
?
This document discusses efficient algorithms for computing the discrete Fourier transform (DFT), specifically the fast Fourier transform (FFT). It covers several FFT algorithms including decimation-in-time, decimation-in-frequency, and the Goertzel algorithm. The decimation-in-time algorithm recursively breaks down the DFT computation into smaller DFTs by decomposing the input sequence. This allows the computation to be performed in O(NlogN) time rather than O(N^2) time for a direct DFT computation. The document also discusses optimizations like in-place computation to reduce memory usage.

boylestad_introduccion_al_analisis_de_circuitos.pdfHederth Ayala Gamarra
?
Este documento introduce el concepto de resistencia el¨¦ctrica. Explica que la resistencia depende de cuatro factores: el material, la longitud, el ¨˘rea de secci¨®n transversal y la temperatura. Define la resistividad como una propiedad del material que determina su resistencia. Presenta una ecuaci¨®n para calcular la resistencia de alambres circulares en funci¨®n de estos factores.linear transfermation.pptx



linear transfermation.pptxUmme habiba
?
This document provides an introduction to linear transformations. It defines a linear transformation as a function that maps one vector space to another while preserving vector addition and scalar multiplication. Key concepts discussed include the domain, co-domain, range, and pre-image of a linear transformation. Examples are given to demonstrate linear transformations and functions that are not linear transformations. The relationship between linear transformations and matrices is also explained.Bahan ajar alin 2 rev 2014 pdf



Bahan ajar alin 2 rev 2014 pdfPawit Ngafani
?
Dokumen tersebut memberikan penjelasan tentang ruang vektor umum, ruang bagian, dan beberapa contohnya. Ruang vektor didefinisikan sebagai himpunan dengan operasi penjumlahan vektor dan perkalian skalar yang memenuhi 10 sifat tertentu. Ruang bagian adalah ruang vektor yang merupakan bagian dari ruang vektor lain dengan operasi yang sama.Koefisien binomial



Koefisien binomialoilandgas24
?
Dokumen tersebut membahas tentang koefisien binomial yang merupakan bilangan yang muncul dari hasil penjabaran ekspresi pemangkatan dua variabel seperti (a + b)n. Dokumen tersebut menjelaskan bahwa koefisien binomial dapat ditentukan menggunakan rumus kombinasi dan dibuktikan menggunakan teorema binomial.Second order homogeneous linear differential equations 



Second order homogeneous linear differential equations Viraj Patel
?
1) The document discusses second order linear homogeneous differential equations, which have the general form P(x)y'' + Q(x)y' + R(x)y = 0.
2) It describes methods for finding the general solution including reduction of order, and discusses the solutions when the coefficients are constants.
3) The general solution depends on the nature of the roots of the auxiliary equation: distinct real roots, repeated real roots, or complex roots.Medan vektor



Medan vektorEthelbert Phanias
?
1. Dokumen tersebut membahas konsep-konsep dasar vektor dan operator-operator vektor yang digunakan dalam medan dan gelombang elektromagnetik, seperti gradien, divergensi, dan curl.
2. Dibahas pula sistem koordinat kartesian, silindris, dan bola yang digunakan untuk merepresentasikan vektor dalam ruang tiga dimensi.
3. Operator-operator vektor digunakan untuk menghitung laju perubahan medan skalar dan vektor.Unit-1 Classification of Signals



Unit-1 Classification of SignalsDr.SHANTHI K.G
?
Classification of signals
Deterministic and Random signals
Continuous time and discrete time signal
Even (symmetric) and Odd (Anti-symmetric) signal
Periodic and Aperiodic signal
Energy and Power signal
Causal and Non-causal signal
Power Point Sistem Persamaan Linear Tiga Variabel



Power Point Sistem Persamaan Linear Tiga Variabelrestu sri rahayu
?
Sistem Persamaan Linear Tiga VariabelContoh soal fisika kuantum



Contoh soal fisika kuantumramainoei
?
1. Persamaan Laplacian dalam koordinat sferis dituliskan. Operator Hamiltonian untuk gerak elektron dalam medan listrik dan magnet juga ditulis.
2. Fungsi gelombang radial untuk atom ditulis dan dinormalisasi. Energi elektron untuk fungsi gelombang tersebut dicari.
3. Spinor untuk elektron dalam medan magnet ditulis. Periode getaran spinor tersebut dicari.
4. Persamaan Schwarz dibuktikan.
5. Nilai eigen dan fungsi eigen tViewers also liked (7)
Ss 2013 midterm



Ss 2013 midtermDharmendra Dixit
?
The document is a mid-semester exam for a signals, systems and controls course. It contains 6 multi-part questions testing various concepts related to continuous-time and discrete-time linear time-invariant systems including impulse responses, step responses, Fourier series, Fourier transforms, and frequency responses. Students are instructed to show all work and write clearly without marking on the exam paper.Ss 2013 midterm



Ss 2013 midtermDharmendra Dixit
?
The document is a mid-semester exam for a signals, systems and controls course. It contains 6 multi-part questions testing various concepts related to continuous-time and discrete-time linear time-invariant systems including impulse responses, step responses, Fourier series, Fourier transforms, and frequency responses. Students are instructed to show all work and can use an open book with the signals and systems textbook.Midsem sol 2013



Midsem sol 2013Dharmendra Dixit
?
The document is a mid-semester exam for a signals, systems and controls course containing 6 questions testing various concepts in continuous and discrete time signals and linear time-invariant systems. The questions cover topics such as linearity properties, time shifting and time reversal, Fourier series representation of signals, Fourier transform properties, convolution, frequency response and impulse response of LTI systems.Signals and Systems by Alan v.oppenheim, alan s. willsky & s.hamid nawab(...



Signals and Systems by Alan v.oppenheim, alan s. willsky & s.hamid nawab(...rbatec
?
This document appears to be a solution manual for an unknown topic. However, the document contains no actual content, it is comprised entirely of blank lines. There is no information that can be summarized from the given document.Signals and system notes



Signals and system notesAyush Mittal
?
This very short document does not contain enough substantive information to summarize in 3 sentences or less. It contains only a few words that do not provide any clear meaning or context.

Mi oppenheim - signals and systems 2ed solucionarioBureau Veritas
?
El sitio web ofrece solucionarios gratuitos de libros universitarios, los cuales contienen todos los ejercicios resueltos y explicados de forma clara para que los estudiantes puedan descargarlos libremente.Solved problems



Solved problemsMulugeta Ashango
?
This document summarizes key concepts in digital and analog communications:
1) It defines source coding, channel encoding/decoding, digital modulation/demodulation, and how digital communication system performance is measured in terms of error probability.
2) Thermal noise in receivers is identified as the dominant source of noise limiting performance in VHF and UHF bands.
3) Storing data on magnetic/optical disks is analogous to transmitting a signal over a radio channel, with similar signal processing used for recovery.
4) Digital processing avoids signal degradation but requires more bandwidth, while analog processing is sensitive to variations but does not lose quality over time.
5) Fourier analysis is used to derive theSimilar to Sns mid term-test2-solution (20)
Rdnd2008



Rdnd2008Gautam Sethia
?
This document discusses the emergence of chimera states, a unique collective state where coherent and incoherent dynamics coexist, in a system of non-locally coupled phase oscillators with propagation delays. It presents the complex Ginzburg-Landau equation (CGLE) model of reaction-diffusion systems and derives a phase reduction with propagation time delays. Numerical simulations and solutions to the self-consistency equation validate the existence of chimera clusters induced by time delays.Adc



AdcGautam Sethia
?
This document discusses the emergence of chimera states, a unique collective state where coherent and incoherent dynamics coexist, in a system of non-locally coupled phase oscillators with propagation delays. It presents the complex Ginzburg-Landau equation (CGLE) model of reaction-diffusion systems and derives a phase reduction with propagation time delays. Numerical simulations and solutions to the self-consistency equation reveal chimera cluster states induced by the time delays.Ss



SsSreenadh Naga Venkata
?
The document contains 8 questions pertaining to signals and systems. It covers topics like Fourier series, Fourier transforms, Laplace transforms, Z-transforms, continuous and discrete time linear time-invariant systems, sampling, and more. Students are required to answer any 5 out of the 8 questions, with all questions carrying equal marks. The questions involve theoretical concepts as well as mathematical problems to test the understanding of fundamental signals and systems concepts.Sns pre sem



Sns pre semprabhatviet
?
This document is a past exam paper for an EEC-404 Signals and Systems course. It contains 3 sections with multiple choice and numerical problems related to signals and systems concepts. Section A contains 10 short answer questions testing definitions, properties and operations related to signals, systems, Laplace transforms, Z-transforms, Fourier transforms, convolution, and block diagrams. Section B contains 5 longer answer questions on properties, Fourier transforms, convolution, correlation and filter responses. Section C contains 5 multi-part problems involving plots, proofs, transforms, convolution, correlation and filter characteristics. The document provides an exam for students to test their understanding of key concepts across time, frequency and transform domains for continuous and discrete time signals and systems.cab2602ff858c51113591d17321a80fc_MITRES_6_007S11_hw04.pdf



cab2602ff858c51113591d17321a80fc_MITRES_6_007S11_hw04.pdfTsegaTeklewold1
?
This document presents several problems related to convolution of discrete-time and continuous-time signals. Problem P4.1 asks the reader to determine the output of a linear time-invariant system given different inputs. Problem P4.2 asks the reader to calculate the discrete-time convolution of two signals. Problem P4.3 asks the reader to calculate the continuous-time convolution of three pairs of signals.cab2602ff858c51113591d17321a80fc_MITRES_6_007S11_hw04.pdf



cab2602ff858c51113591d17321a80fc_MITRES_6_007S11_hw04.pdfTsegaTeklewold1
?
This document presents several problems related to convolution of discrete-time and continuous-time signals. Problem P4.1 asks the reader to determine the output of a linear time-invariant system given different inputs. Problem P4.2 asks the reader to calculate the discrete-time convolution of two signals. Problem P4.3 asks the reader to calculate the continuous-time convolution of three pairs of signals.Convolution problems



Convolution problemsPatrickMumba7
?
This document presents several problems related to convolution of discrete-time and continuous-time signals. Problem P4.1 asks the reader to determine the output of a linear time-invariant system given different inputs. Problem P4.2 asks the reader to calculate the discrete-time convolution of two signals. Problem P4.3 asks the reader to calculate the continuous-time convolution of signals.Review for the Third Midterm of Math 150 B 11242014Probl.docx



Review for the Third Midterm of Math 150 B 11242014Probl.docxjoellemurphey
?
Review for the Third Midterm of Math 150 B 11/24/2014
Problem 1
Recall that 1
1?x =
ˇĆˇŢ
n=0 x
n for |x| < 1.
Find a power series representation for the following functions and state the radius of
convergence for the power series
a) f(x) = x
2
(1+x)2
.
b) f(x) = 2
1+4x2
.
c) f(x) = x
4
2?x.
d) f(x) = x
1+x2
.
e) f(x) = 1
6+x
.
f) f(x) = x
2
27?x3 .
Problem 2
Find a Taylor series with a = 0 for the given function and state the radius of conver-
gence. You may use either the direct method (definition of a Taylor series) or known
series.
a) f(x) = ln(1 + x)
b) f(x) = sin x
x
c) f(x) = x sin(3x).
Problem 3
Find the radius of convergence and interval of convergence for the series
ˇĆˇŢ
n=1
(x+2)n
n4n
.
Ans. Radius r=2,
ˇĚ
2 ? 2 < x <
ˇĚ
2 + 2. Problem 4
Find the interval of convergence of the following power series. You must justify your
answers.
ˇĆˇŢ
n=0
n2(x+4)n
23n
.
Ans. ?12 < x < 4.
Problem 5
For the function f(x) = 1/
ˇĚ
x, find the fourth order Taylor polynomial with a=1.
Problem 6
A curve has the parametric equations
x = cos t, y = 1 + sin t, 0 ˇÜ t ˇÜ 2¦Đ
a) Find dy
dx
when t = ¦Đ
4
.
b) Find the equation of the line tangent to the curve at t = ¦Đ/4. Write it in y = mx+b
form.
c) Eliminate the parameter t to find a cartesian (x, y) equation of the curve.
d) Using (c), or otherwise identify the curve.
Problem 7
State whether the given series converges or diverges
a)
ˇĆˇŢ
n=0 (?1)
n+1 n22n
n!
.
b)
ˇĆˇŢ
n=0
n(?3)n
4n?1
.
c)
ˇĆˇŢ
n=1
sin n
2n2+n
.
Problem 8
1
Approximate the value of the integral
ˇŇ 1
0
e?x
2
dx with an error no greater than 5ˇÁ10?4.
Ans.
ˇŇ 1
0
e?x
2
dx = 1 ? 1
3
+ 1
5.2!
? 1
7.3!
+ ... +
(?1)n
(2n+1)n!
+ .... n ˇÝ 5,
for n=5
ˇŇ 1
0
e?x
2
dx ˇÖ 1 ? 1
3
+ 1
5.2!
? 1
7.3!
+ 1
9.4!
? 1
11.5!
ˇÖ 0.747.
Problem 9
Find the radius of convergence for the series
ˇĆˇŢ
n=1
nn(x?2)2n
n!
.
Ans. R = 1ˇĚ
e
.
Problem 10
Let f(x) =
ˇĆˇŢ
n=0
(x?1)n
n2+1
.
a) Calculate the domain of f.
b) Calculate f ˇä(x).
c) Calculate the domain of f ˇä.
Problem 11
Let f(x) =
ˇĆˇŢ
n=0
cos n
n!
xn.
a) Calculate the domain of f.
b) Calculate f ˇä(x).
c) Calculate
ˇŇ
f(x)dx.
Problem 12
Using properties of series, known Maclaurin expansions of familiar functions and their
arithmetic, calculate Maclaurin series for the following.
a) ex
2
b) sin 2x
c)
ˇŇ
x5 sin xdx
d) cos x?1
x2
e)
d((x+1) tan?1(x))
dx
Problem 13
Calculate the Taylor polynomial T5(x), expanded at a=0, for
f(x) =
ˇŇ x
0
ln |sect + tan t|dt.
Ans. T5(x) =
x2
2
+ x
4
4!
.
Problem 14
Suppose we only consider |x| ˇÜ 0.8. Find the best upper bound or maximum value
you can for¨O¨O¨Osin x ? (x ? x33! + x55! )¨O¨O¨O
Same question: If
(
x ? x
3
3!
+ x
5
5!
)
is used to approximate sin x for |x| ˇÜ 0.8. What is
the maximum error? Explain what method you are using.
Problem 15
The Taylor polynomial T5(x) of degree 5 for (4 + x)
3/2 is
(4 + x)3/2 ˇÖ 8 + 3x + 3
16
x2 ? 1
128
x3 + 3
4096
x4 ? 3
32768
x5.
a) Use this polynomial to find Taylor polynomials for (4 + ...Assignment6



Assignment6asghar123456
?
This document contains instructions for 5 assignment questions involving numerical integration and solving differential equations. Question 1 involves using the quad function to evaluate several integrals. Question 2 involves using quad to evaluate Fresnel integrals and plot the results. Question 3 involves using Monte Carlo methods to estimate volumes and double integrals. Question 4 involves using Euler's method to solve an initial value problem and analyze errors. Question 5 involves using lsode to solve a system of differential equations modeling atmospheric circulation and experimenting with initial conditions.Ma8353 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS



Ma8353 TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONSBIBIN CHIDAMBARANATHAN
?
This document appears to be an exam for a third semester engineering course covering topics in transforms and partial differential equations. It contains 15 multiple choice and numerical response questions testing knowledge of various transforms (Fourier, Laplace, Z) and partial differential equations (heat, wave, etc). The questions cover topics such as singular integrals, Fourier series behavior at discontinuities, sketching even/odd extensions, solving PDEs using separation of variables, convolution theorems, and applications of transforms.EC8352-Signals and Systems - Laplace transform



EC8352-Signals and Systems - Laplace transformNimithaSoman
?
The document discusses the Laplace transform and its properties. It begins by introducing Laplace transform as a tool to transform signals from the time domain to the complex frequency (s-domain). It then provides the Laplace transforms of some elementary signals like impulse, step, ramp functions. It discusses properties like linearity, time shifting, frequency shifting. It also covers the region of convergence, causality, stability analysis using poles in the s-plane. The document provides examples of finding the Laplace transform and analyzing signals based on properties like time shifting and frequency shifting. In the end, it summarizes the convolution property and the initial and final value theorems.Es400 fall 2012_lecuture_2_transformation_of_continuous_time_signal.pptx



Es400 fall 2012_lecuture_2_transformation_of_continuous_time_signal.pptxumavijay
?
This document outlines transformations that can be applied to continuous-time signals, including time reversal, time scaling, time shifting, and amplitude transformations. It also discusses properties of even and odd signals. Time reversal flips the signal across the time axis. Time scaling stretches or compresses the time axis. Time shifting slides the signal along the time axis. Amplitude transformations multiply the signal by a constant and add an offset. The product of two even signals is even, while the product of an even and odd signal is odd.Mid term solution



Mid term solutionGopi Saiteja
?
This document contains the mid-term exam for the Communication Networks course EE 333. The exam consists of 3 questions covering topics related to communication networks including:
1) Analytic expressions for the time taken for transmission of N packet blocks in an ARQ scheme with propagation delay. Expressions are given for N=1,2,3.
2) Code words, circular shifts, and error detection for CRC codes. An example error pattern is shown to be undetectable.
3) A Markov chain model for a communication channel and derivation of the maximum success probability.Signals Processing Homework Help



Signals Processing Homework HelpMatlab Assignment Experts
?
The document provides homework problems and solutions related to signals processing. It includes problems on determining the frequency and period of signals, properties of even and odd signals, sampling of continuous signals, and periodicity of sums of signals. It also provides detailed solutions and explanations to each problem.Chapter 3 (maths 3)



Chapter 3 (maths 3)Prathab Harinathan
?
1) The document discusses solving partial differential equations using variable separation. It presents the one-dimensional wave equation and solves it using variable separation.
2) It derives three cases for the solution based on whether k is positive, negative, or zero. It then presents the general solution as a summation involving sines and cosines.
3) It applies the general solution to two example problems of a vibrating string, finding the displacement as a function of position and time by satisfying the boundary conditions.09 a1bs01 mathematics-1



09 a1bs01 mathematics-1jntuworld
?
This document contains 8 questions related to mathematics. Question 2 asks students to (a) form a differential equation by eliminating arbitrary constants from an expression involving logarithms, (b) solve a differential equation, and (c) calculate the temperature of a body cooling over time. Question 3 asks students to (a) find the Laplace transform of a periodic function and (b) solve a differential equation using Laplace transforms.8fbf4451c622e6efbcf7452222d21ea5_MITRES_6_007S11_hw02.pdf



8fbf4451c622e6efbcf7452222d21ea5_MITRES_6_007S11_hw02.pdfTsegaTeklewold1
?
This document provides recommended problems related to signals and systems. Problem P2.1 involves determining the frequency and period of cosine signals with different phase shifts. Problem P2.2 is similar but with discrete-time cosine signals. Problem P2.3 involves sketching shifted and scaled versions of a sample discrete-time signal. The remaining problems involve determining whether signals are even, odd, or neither; evaluating sums; exploring properties of periodic signals; and analyzing sampled continuous-time signals.Signal and Systems part i



Signal and Systems part iPatrickMumba7
?
This document provides recommended problems related to signals and systems. Problem P2.1 involves determining the frequency and period of cosine signals with different phase shifts. Problem P2.2 is similar but with discrete-time cosine signals. Problem P2.3 involves sketching shifted and scaled versions of a sample discrete-time signal. The remaining problems involve determining whether signals are even, odd, or neither; evaluating sums; exploring periodicity of signal sums; properties of even and odd signals; and sampling a continuous-time signal.Engr 213 final 2009



Engr 213 final 2009akabaka12
?
This document contains a 9 question final exam for an applied ordinary differential equations engineering course. The questions cover a range of topics including: finding general and particular solutions to 1st and 2nd order differential equations using various methods; solving initial value problems; solving systems of differential equations; power series solutions; and modeling an LRC circuit with a differential equation. Students are given 3 hours to complete the exam worth a total of 100 points.More from cheekeong1231 (8)
Sns slide 1 2011



Sns slide 1 2011cheekeong1231
?
The document provides information about a signals and systems course taught by Mr. Koay Fong Thai. It includes announcements about course policies, assessments, and schedule. Students are advised to ask questions, work hard, and submit assignments on time. The use of phones and laptops in class is strictly prohibited. The course aims to introduce signals and systems analysis using various transforms. Topics include signals in the time domain, Fourier transforms, Laplace transforms, and z-transforms. Reference books and a lecture schedule are also provided.Chap3



Chap3cheekeong1231
?
This document provides an overview of programming concepts and control structures. It discusses pseudocode and flowcharts as tools for designing algorithms to solve problems. Different control structures are introduced, including sequence, selection, and repetition structures. Examples are provided to illustrate these concepts such as getting user input, making decisions, and repeating steps. The key learning goals are to understand how to design algorithms using control structures and represent them using pseudocode and flowcharts.Bjt tut 9 1(2003)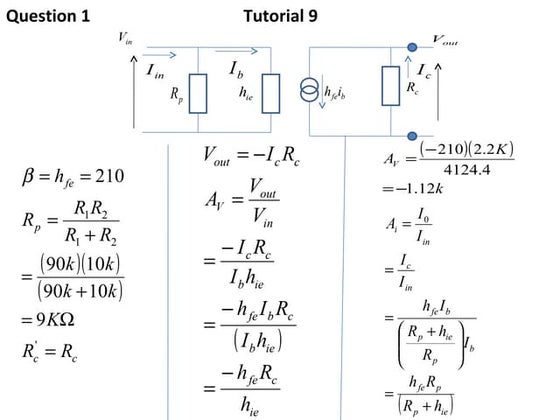



Bjt tut 9 1(2003)cheekeong1231
?
The document discusses key concepts in amplifiers including:
1) Gain is defined as the ratio of output to input voltage, current, or power.
2) An amplifier's frequency response is defined by its change in gain or phase shift over a range of input frequencies.
3) Bandwidth is defined as the difference between the upper and lower cutoff frequencies of an amplifier.Revision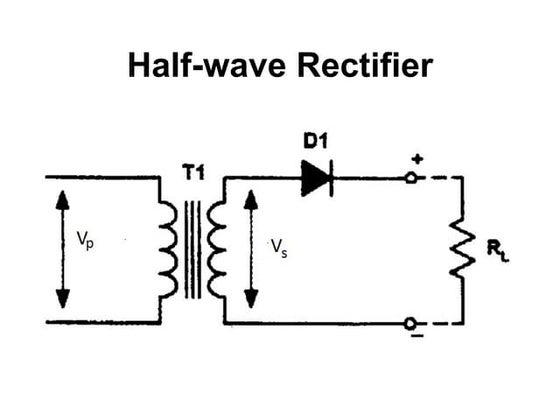



Revisioncheekeong1231
?
The document provides information on different types of rectifiers including half-wave, bi-phase, and bridge rectifiers. It discusses their output characteristics such as peak output, average output, peak inverse voltage, and output frequency. The document also covers BJT biasing techniques including base, emitter, voltage divider, and collector feedback bias. It summarizes the h-parameters used in the hybrid-pi model and provides the common emitter h-parameter equivalent circuit.Revision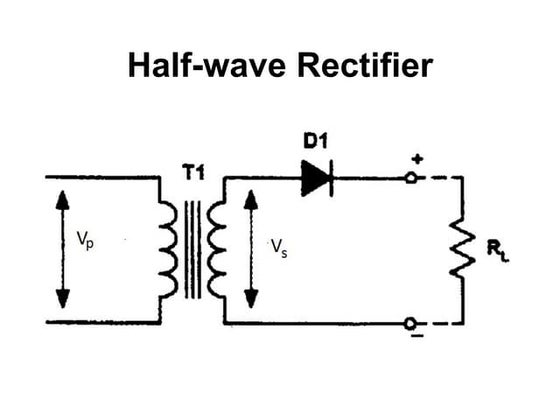



Revisioncheekeong1231
?
This document provides information on various topics related to semiconductor devices and transistor amplifiers, including:
- Types of rectifiers such as half-wave, full-wave, and bridge rectifiers.
- BJT biasing configurations like base, emitter, voltage divider, and collector feedback bias.
- BJT amplifier configurations including common emitter, common base, and common collector.
- Transistor parameters like current gain and their effects on circuit operation.
- Hybrid-pi and h-parameter transistor models for AC analysis.
So in summary, it discusses rectifier circuits, transistor biasing methods, amplifier configurations, key transistor parameters, and transistor modeling for analysis of small-Standard formula



Standard formulacheekeong1231
?
This document contains standard formulas used in electronics. It includes formulas for peak voltage, voltage ripple, DC voltage, voltage gain, current gain, transconductance, drain current, voltage amplification, and input impedance. The formulas contain variables like Vp, Vs, R, L, C, f, XC, Vr, ¦Â, gm, ID, VGS, RL, RC, hfe, Rp, and hie.Et1 practical final examination



Et1 practical final examinationcheekeong1231
?
This document contains 4 questions related to electronics concepts. Question 1 covers semiconductor materials, current carriers, doping, pn junctions, and biasing. Question 2 covers ripple voltage, ripple factor, and calculating branch currents in a diode circuit. Question 3 covers diode clippers, clampers, line regulation, and LED operation conditions. Question 4 covers relationships between DC current gain parameters, transistor biasing, calculating voltage and current gain based on transistor parameters, and determining current and voltage in a transistor circuit.Sns mid term-test2-solution
- 1. PSDC ENGINEERING DIPLOMA ASSESSMENT Signals And Systems ¨C Mid-Term Test 2 (B16 CE/B17 EEA&EEB) 7th January 2009, Wednesday 2:00pm ¨C 5:00pm (3 hours) Question 1 (Signals and Systems) (a) Determine whether the following signals are periodic or aperiodic. If it is a periodic signal, determine its power. (i) x[n] = 2cos(?¦Đn) + sin(?¦Đn) (ii) x(t) = Odd{cos(2¦Đt)} (b) If x(t) = (t2 ¨C 1) [u(t) ¨C u(t¨C4)], (i) Sketch x(t) (ii) Sketch x(t ¨C 2) (iii) Sketch x(¨C3t ¨C 2) (iv) Sketch Even{x(t ¨C 2)} (c) Determine the following systems are casual, linear and time-invariant. (i) y[n] = 3x2[¨C2n] (ii) y(t) = cos (t+ ? ¦Đ) x(t) Question 2 (Convolution) (a) Evaluate the convolution sum for y[n] = x[n]?h[n], where x[n] and h[n] are shown in Fig. Q2 (a). Fig. Q2 (a) (b) Define the convolution of two signals x(t) and h(t). Then, compute the convolution integral for y(t) = x(t)?h(t) of the following signals: h(t) = e¨C3tu(t) and x(t) = e¨C3tu(t¨C1). 1
- 2. PSDC ENGINEERING DIPLOMA ASSESSMENT Question 3 (Laplace Transform) (a) Define Bilateral (two-sided) Laplace Transform. (b) Consider the signal, x(t) = e¨C3tu(t). Find the Laplace transform of x(t) with the associated region of convergence (ROC). (c) Consider a continuous-time LTI system described by d 2 y( t ) dy( t ) dx( t ) 2 ?3 ? 2 y( t ) = ?3 + x( t ) dt dt dt Using the shifting property, find the unit impulse response h(t). Question 4 (z-Transform) (a) Define Bilateral (two-sided) z-Transform. (b) Consider the signal, x[k] = aku[k]. Find the z-transform of x[k] with the associated region of convergence (ROC). (c) Consider a discrete-time LTI system described by y[k] ¨C y[k¨C1] ¨C 2 y[k¨C2] = x[k] + 2 x[k¨C1] + 2 x[k¨C2] Using the shifting property, find the unit impulse response h[k]. "Learning without thought is useless; thought without learning is dangerous." ѧ¶ř˛»ËĽÔňŘč,ËĽ¶ř˛»Ń§Ôň´ů. 2












