Soal Jawab Kalkulus Model Pertumbuhan Gompertz
- 1. Tugas Kalkulus Model Pertumbuhan Gompertz Dadang Amir Hamzah May 10, 2013 Kurva pertumbuhan Gompertz digunakan untuk mempelajari pertum- buhan populasi. Kurva dari model ini mempunyai sifat yang serupa dengan kurva model pertumbuhan logistik. Kurva pertumbuhan Gompertz dinyata- kan dengan N(t) = K exp(aeŌłÆbt ), dengan t Ōēź 0, dan K, b adalah konstanta-konstanta positif. a. Tunjukkan bahwa N(0) = KeŌłÆa dan apabila N0 = N(0) maka a = ln K N0 . Jawab: Diketahui kurva pertumbuhan Gompertz adalah N(t) = K exp(ŌłÆaeŌłÆbt ), (1) untuk t Ōēź 0, dan K, b konstanta positif. N(0) terjadi ketika t = 0, de- ngan mensubstitusi t = 0 ke persamaan (1) didapat N(0) = K exp(ŌłÆa). Kemudian dengan menuliskan N(0) = N0 dan dengan menggunakan sifat eksponen didapat a = ln K N0 . 1
- 2. b. Tunjukkan bahwa y = K adalah asimtot datar. Kemudian tunjukkan pula bahwa jika N0 < K maka N(t) < K, Jika N0 = K maka N(t) = K, dan jika N0 > K maka N(t) > K. Jawab: Akan ditunjukkan bahwa garis y = K adalah asimtot datar dari Kurva N(t), artinya harus ditunjukkan bahwa lim tŌåÆŌł× N(t) = K. Perhatikan bahwa N(t) = K exp(ŌłÆaeŌłÆbt ). Apabila kita limitkan untuk t ŌåÆ Ōł× akan didapat limtŌåÆŌł× K exp(ŌłÆaeŌłÆbt = K exp(ŌłÆaeŌł× ) = K exp(0) = K. Jadi terbukti bahwa garis y = K adalah asimtot datar dari kurva N(t). Selanjutnya akan ditunjukkan jika N0 < K maka Nt < K. Karena K > 0 maka N0 > 0, akibatnya N0 < K dengan mengambil ln dikedua ruas ln N0 < ln K ln K ŌłÆ ln N0 > 0 ln K N0 > 0, (Karena a = ln K N0 ) a > 0, (kalikan kedua ruas dengan ŌłÆ eŌłÆbt ) ŌłÆaeŌłÆbt < 1, (eksponenkan kedua ruas kemudian kalikan dengan K) K exp(ŌłÆaeŌłÆbt ) < K N(t) < K. Jadi terbukti bahwa jika N0 < K maka Nt < K. Dengan cara yang sama dapat juga ditunjukkan bahwa jika N0 = K maka Nt = K, dan 2
- 3. jika N0 > K maka Nt > K. (Catatan: Hati-hati dengan tanda ŌĆØ > ŌĆØ dan ŌĆØ < ŌĆØ) c. Tunjukkan bahwa dN dt = bN (ln K ŌłÆ ln N) dan d2 N dt = b dN dt (ln K ŌłÆ ln N ŌłÆ 1). Jawab: Perhatikan bahwa N(t) = K exp(ŌłÆaeŌłÆbt ) , (dengan menurunkan kedua ruas terhadap t) dN dt = ab eŌłÆby K exp(ŌłÆaeŌłÆbt ) = ab eŌłÆby N = bN aeŌłÆby = bN (ln K ŌłÆ ln N). Jadi terbukti bahwa dN dt = bN (ln K ŌłÆ ln N). Untuk mendapatkan d2N dt turunkan dN dt terhadap t sehigga d2N dt = b dN dt (ln K ŌłÆ ln N) + bN(0 ŌłÆ 1 N dN dt ) = b dN dt (ln K ŌłÆ ln N ŌłÆ 1). Jadi terbukti bahwa d2N dt = b dN dt (ln K ŌłÆ ln N ŌłÆ 1). d. Gunakan hasil pada b dan c untuk menunjukkan jika N0 < K maka N(t) naik sempurna dan jika N0 > K maka N(t) turun sempurna. Jawab: Kurva N(t) naik jika dN dt > 0. Akan ditunjukkan bahwa jika N0 < K maka dN dt > 0. Pada soal bagian b telah ditunjukkan bahwa jika N0 < K maka N < K. 3
- 4. Selanjutnya perhatikan bahwa untuk N < K berlaku ln N < ln K ln K ŌłÆ ln N > 0, (tambahkan kedua ruas dengan ŌłÆ ln N) bN (ln K ŌłÆ ln N) > 0, (kalikan kedua ruas dengan bN) dN dt > 0. Jadi terbukti bahwa jika N0 < K maka N(t) naik sempurna. Dengan cara yang sama perhatikan bahwa N > K ln N > ln K ln K ŌłÆ ln N < 0 bN (ln K ŌłÆ ln N) < 0 dN dt < 0. Jadi terbukti bahwa jika N0 > K maka N(t) turun sempurna. e. Saat t berapakah kurva N(t) melalui titik belok? Diskusikan kecekun- gan dan kecembungannya? Jawab : Dengan menggunakan uji turunan kedua titik belok kurva N(t) dicapai di t yang memenuhi d2N dt = 0, kemudian kurva N(t) cekung keatas jika d2N dt > 0 dan kurva N(t) cekung kebawah jika d2N dt < 0. Dari soal c diketahui d2N dt = b dN dt (ln K ŌłÆ ln N ŌłÆ 1). Titik belok dicapai di t yang memenuhi d2 N dt = b dN dt (ln K ŌłÆ ln N ŌłÆ 1) = 0 Hal ini mungkin terjadi hanya untuk ln K ŌłÆ ln N ŌłÆ 1 = 0 4
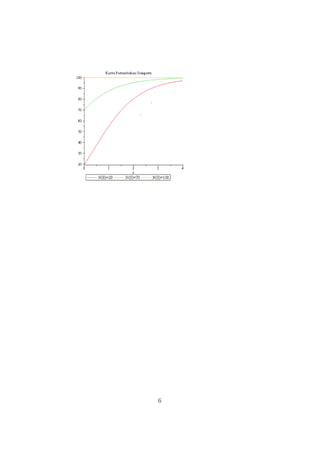
- 5. yakni ln N + 1 = ln K ln K ŌłÆ aeŌłÆbt + 1 = ln K ŌłÆaeŌłÆbt + 1 = 0 1 = aeŌłÆbt ebt = a ln a = bt t = ln a b . Jadi titik belok dari N(t) terjadi saat t = ln a b . Kemudian dengan cara yang sama d2N dt2 > 0 dicapai saat t < ln a b dan d2N dt2 dicapai saat t > ln a b . Artinya kurva N(t) terbuka keatas saat t < ln a b kemudian belok saat t = ln a b dan terbuka kebawah saat t > ln a b . e. Gambarkan kurva N(t) untuk K = 100 , b = 1 dan kondisi-kondisi berikut: i. N0 = 20. ii. N0 = 70. iii. N0 = 150. jawab: 5
- 6. 6