Soal permutasi, kombinasi dan peluang
- 1. Contoh Soal Permutasi, Kombinasi dan Peluang Oleh : Aniza Dwi Anggraeni (292011238) Tri Mulyani (292011249) Nurkholis (292011271)
- 2. 4.8 Ada sebuah ruangan yang lantainya berukuran 8 Ă— 2 satuan, seperti pada gambar di bawah ini. Agus ingin menutupi lantai tersebut dengan ubin yang berbentuk domino. Setiap ubin dapat diletakkan secara tegak maupun mendatar (lihat gambar). Ada berapa cara pemasangan ubin yang mungkin untuk menutupi seluruh lantai tersebut? Ingat tidak boleh ada celah dan setiap ubin tidak boleh saling tumpah tindih!
- 5. 4.8 Dengan pemberian nomer sesuai urutan, maka akan lebih mudah menghitungnya JADI ADA 28 CARA PEMASANGAN UBIN 21 22 23 24 25 26 27 28
- 6. Noether mempunyai anak timbangan 1 kg, 3 kg, 9 kg, dan 27 kg dan sebuah timbangan dua lengan. Dengan alat-alat ini, ia dapat mengukur berat berapa kg? (1.9)
- 7. 1kg 3kg 9kg 27kg
- 8. 1kg 1 kg 1
- 9. 3kg 3 kg 2
- 10. 9kg 9 kg 3
- 11. 27kg 27 kg 4
- 12. 1kg + 9kg 10 kg 5
- 13. 1kg + 3kg 4 kg 6
- 14. 1kg + 27kg 28 kg 7
- 15. 3kg + 9kg 12 kg 8
- 16. 3kg + 27 kg 30 kg 9
- 17. 9kg + 27kg 36 kg 10
- 18. 1kg + 3kg + 9kg 13 kg 11
- 19. 1kg + 3kg + 27kg 31 kg 12
- 20. 1kg + 9kg + 27kg 37 kg 13
- 21. 3kg + 9kg + 27kg 39 kg 14
- 22. 1kg + 3kg + 9kg + 27kg 40 kg 15
- 23. 3kg 2 kg 1kg 16
- 24. 8 kg 1kg 9kg 17
- 26. 11 kg 1kg 3kg + 9kg 19
- 27. 29 kg 1kg 3kg + 27kg 20
- 28. 35 kg 1kg 9kg + 27kg 21
- 29. 38 kg 1kg 3kg + 9kg + 27kg 22
- 30. 9kg 6 kg 3kg 23
- 32. 7 kg 3kg 1kg + 9kg 25
- 33. 25 kg 3kg 1kg + 27kg 26
- 34. 33 kg 3kg 9kg + 27kg 27
- 35. 34 kg 3kg 1kg + 9kg + 27kg 28
- 37. 19 kg 9kg 1kg + 27kg 30
- 38. 21 kg 9kg 3kg + 27kg 31
- 39. 22 kg 9kg 1kg + 3kg +27kg 32
- 40. 5 kg 1kg + 3kg 9kg 33
- 41. 27kg 23 kg 1kg + 3kg 34
- 42. 32 kg 1kg + 3kg 9kg + 27kg 35
- 43. 27kg 17 kg 1kg + 9kg 36
- 44. 15 kg 3kg + 9kg 27kg 37
- 45. 16 kg 3kg + 9kg 1kg + 27kg 38
- 46. 14 kg 1kg + 3kg + 9kg 27kg 39
- 47. 20 kg 1kg + 9kg 3kg + 27kg 40
- 48. Jadi, Noether dapat mengukur 40 berat, yaitu berat 1-40 kg
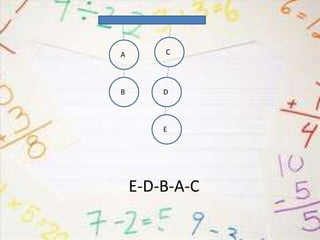
- 49. SOAL A B C D E 49 Paskal dan Lebek bermain tembak-tembakan dengan lima buah target: A, B, C, D, dan E yang digantung (lihat gambar). Seorang pemain harus menembak semua target satu demi satu, dimulai dari target yang paling bawah pada salah satu kolom. Dengan berapa cara yang berbeda target-target tersebut dapat ditembak?
- 50. • Paskal dan Lebek bermain tembak-tembakan dengan lima buah target: A, B, C, D, dan E yang digantung. A B C D E TARGET TARGET
- 51. KETENTUAN • Seorang pemain harus menembak semua target satu demi satu • Dimulai dari target yang paling bawah pada salah satu kolom. target awal A B C D E
- 52. Ada berapa cara yang berbeda target-target tersebut dapat ditembak? A B C D E
- 53. JAWAB:
- 64. Jadi terdapat 10 cara yang berbeda untuk menembak semua target
- 65. Soal 5,9 Fibo berulang tahun ke 12. Fibo ingin menyusun dua belas lilin di atas kue ulang tahunnya dengan cara yang unik. Lilin-lilin tersebut harus terletak dalam 6 buah garis, empat lilin pada setiap garisnya. Ayo coba gambarkan beberapa cara penyusunan yang mungkin!
- 66. Jawaban Bagaimana ya gambarnya? Ayo coba kita gambarkan beberapa cara penyusunannya... Nah lilinnya ada 12, sudah tahu cara menghitungnya kan.. Coba gambar yang lainnya bagaimana ? 1
- 67. 2 3 4 5
- 68. 6 7 8 9
- 69. 10 11 12 13
- 70. 14 15 16 17
- 71. 18 19 20 21
- 72. 22 23 24 25
- 73. 26 27 28 29
- 74. 30 31 32 33
- 75. 34 35 36 37
- 76. 38 39 40 41
- 77. 42 43 44 45
- 78. 46 47 48 49
- 79. 51 50 Jadi, ada kemungkinan 51 cara penyusunan lilin diatas kue ulang tahun.
- 80. Soal 8.2 Ada empat anak yang memakai topi. Ketika hendak masuk kelas, mereka melepaskan topinya, dan meletakkannya ke dalam sebuah keranjang. Ketika mereka hendak pulang, mereka mengambil topi. Namun tidak ada satu anak pun yang mengambil topi miliknya. Ada berapa cara hal ini dapat terjadi?
- 81. SISWA A B C D TOPI 1 2 3 4 DAFTAR KEMUNGKINAN ANAK MEMAKAI TOPI A1 B1 C1 D1 A2 B2 C2 D2 A3 B3 C3 D3 A4 B4 C4 D4 ELIMINASI ANAK YANG MEMAKAI TOPI MILIKNYA SENDIRI A1 B1 C1 D1 A2 B2 C2 D2 A3 B3 C3 D3 A4 B4 C4 D4 JADI ADA 12 CARA MEREKA TIDAK MENGAMBIL TOPI MILIKNYA SENDIRI
- 82. Kita misalkan nama anak A,B,C, dan D. Mereka meletakkan topi dalam keranjang A B C D
- 83. A B C D Topi A bisa dipakai B,C, dan D = 3 cara Topi B bisa dipakai C, D, dan A = 3 cara Topi C bisa dipakai D, A, dan B = 3 cara Topi D bisa dipakai A, B, dan C = 3 cara Jadi ada 3 + 3 + 3 + 3 = 12 cara
- 84. A B C D
- 85. A B C D
- 86. A B C D
- 87. A B C D
- 88. Dari kemungkinan diatas setiap anak dapat mengambil 3 topi yang bukan miliknya. Jadi ada 12 cara yang dapat terjadi untuk 4 anak tersebut dalam mengambil topi .
- 89. • 1.3 Lima buah lingkaran dihubungkan dengan ruas garis seperti pada gambar berikut: • Jon hendak mewarnai setiap lingkaran dengan warna- warna yang tersedia, yaitu biru, kuning, dan merah. • Syaratnya, dua lingkaran yang dihubungkan dengan ruas garis tidak boleh mempunyai warna yang sama. • Ada berapa cara pewarnaan yang mungkin?
- 90. 1
- 95. ADA 33 CARA PEWARNAAN
- 96. Goras mempunyai empat lembar uang Rp.1.000,00 dan tiga lembar uang Rp.5.000,00. Berapa banyak kombinasi nilai uang yang dapat dibentuk Goras, dengan syarat ia harus menggunakan setidaknya satu lembar uang? SOAL
- 97. Strategi Kombinasi Goras memiliki Berapa banyak kombinasi yang dapat di buat Goras??
- 98. c = Menggunakan 1 lembar uang 7 1 7! 1!61 = 7.6! 1.6! = 7 Jadi ada 7 cara
- 99. c = Menggunakan 2 lembar uang 7 2 7! 2!51 = 7.6.5! 2.1.5! = 42 Jadi ada 21 cara 2 = 21
- 100. c = Menggunakan 3 lembar uang 7 3 7! 3!41 = 7.6.5.4! 3.2.1.4! = 35 Jadi ada 35 cara
- 101. c = Menggunakan 4 lembar uang 7 4 7! 3!41 = 7.6.5.4! 3.2.1.4! = 35 Jadi ada 35 cara
- 102. c = Menggunakan 5 lembar uang 7 5 7! 2!51 = 7.6.5! 2.1.5! = 42 Jadi ada 21 cara 2 = 21
- 103. c = Menggunakan 6 lembar uang 7 6 7! 1!61 = 7.6! 1.6! Jadi ada 7 cara = 7
- 104. c = Menggunakan 7 lembar uang 7 7 7! 71 = Jadi ada 1 cara 1
- 105. Jadi kombinasi yang terbentuk
- 106. (4,10). Sebuah tromino berbentuk I adalah susunan tiga persegi seperti ditunjuk pada gambar.
- 107. Sebuah kartu tromino berbentuk I dapat menutup 3 buah persegi pada sebuah papan catur berukuran 4x4. Ada 16 cara menempatkan tromino tersebut, yaitu 8 cara dalam posisi tegak dan 8 cara dalam posisi mendatar. Ada berapa cara meletakkan tromino ini pada papan catur raksasa yang berukuran 2006x2006?
- 108. Jawab : • Jumlaha kotak = 2006 x 2006 = 4.024.036 kotak • 3 susun kotak menjadi C(4.024.036,1) = 4.024.036 ! 1!( 4.024.036 – 1) ! • = 4.024.036 . 4.024.035 ! 1! . 4.024.035 ! = 4.024.036 cara = 2.012.018 cara dalam posisi tegak dan 2.012.018 cara dalam posisi mendatar
- 109. Soal Latihan Ada empat buah warna : merah, kuning, hijau, dan biru. Rino hendak mewarnai daerah-daerah dalam gambar di bawah ini, sedemikian hingga daerah yang bertetangga mempunyai warna yang berbeda. Ada berapa cara pewarnaan yang mungkin? 5. Strategi 1
- 110. 1 2
- 111. 3 4
- 112. 5 6
- 113. 8 7
- 114. 9 1 0
- 115. 11 1 2
- 116. 1 3 1 4
- 117. 1 5 1 6
- 118. 1 7 1 8
- 119. 1 9 2 0
- 120. 2 1 2 2
- 121. 2 3 2 4
- 122. Ada delapan orang di dalam suatu kelas. Setiap orang saling berjabat tangan satu sama lain. Ada berapa jabat tangan yang terjadi? (4.1)
- 124. Mendaftar A B C D E F G H A - BA CA DA EA FA GA HA B AB - CB DB EB FB GB HB C AC BC - DC EC FC GC HC D AD BD CD - ED FD GD HD E AE BE CE DE - FE GE HE F AF BF CF DF EF - GF HF G AG BG CG DG EG FG - HG H AH BH CH DH EH FH GH - Jadi, jabat tangan yang terjadi ada 28
- 125. C 8 2 8! 2!(8-2)! = 8! 2!.6! = 8.7.6! 2!.6! Cara 2 4 4.7= = 28=
- 126. Soal • Tara, Dewi, dan Noni melakukan permainan melempar koin. Dua buah koin Rp100,00 dilempar sekali. Jika hasilnya 2 garuda, Tara menang. Jika hasilnya 1 garuda dan 1 kakak tua, Dewi menang. Jika hasilnya 2 kakak tua, Noni menang. Berapakah peluang • a) Dewi menang • b) Tara menang
- 127. Peluang Tara menang adalah n(A)/n(S) = 1/4 Peluang Dewi menang adalah n(A)/n (S)= 2/4=1/2 n (S) = 4
- 128. Soal • Fibo memiliki dua buah dadu. Satu dadu terdiri dari angka 2, 3, 5, 7, 11, dan 13. • Dadu yang satu lagi terdiri dari angka 4, 6, 8, 10, 12, dan 14. Berapa peluang munculnya • a) jumlah kedua mata dadu sama dengan 10 • b) jumlah kedua mata dadu sama dengan 30
- 129. Mata dadu pertama Matadadukedua 2 3 5 7 11 13 4 (2, 4) (3,4) (5,4) (7,4) (11,4) (13,4) 6 (2, 6) (3,6) (5,6) (7,6) (11, 6) (13,6) 8 (2, 8) (3,8) (5,8) (7,8) (11,8) (13,8) 10 (2,10) (3,10) (5,10) (7,10) (11, 10) (13,10) 12 (2,12) (3,12) (5,12) (7,12) (11,12) (13,12) 14 (2,14) (3,14) (5,14) (7,14) (11,14) (13,14) Keterangan : = jumlah kedua mata dadu sama dengan 10 Jadi peluang munculnya jumlah kedua mata dadu adalah sama dengan 10 1 36 A.
- 130. Sedangkan peluang munculnya jumlah kedua mata dadu sama dengan 30 adalah 0 atau disebut juga kemustahilan Mata dadu pertama Matadadukedua 2 3 5 7 11 13 4 (2, 4) (3,4) (5,4) (7,4) (11,4) (13,4) 6 (2, 6) (3,6) (5,6) (7,6) (11, 6) (13,6) 8 (2, 8) (3,8) (5,8) (7,8) (11,8) (13,8) 10 (2,10) (3,10) (5,10) (7,10) (11, 10) (13,10) 12 (2,12) (3,12) (5,12) (7,12) (11,12) (13,12) 14 (2,14) (3,14) (5,14) (7,14) (11,14) (13,14)