�ݺ�ߣ

Solid state
Crystalline solids
Amorphous
solids
2

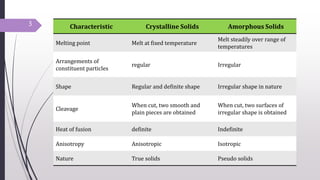
3 Characteristic Crystalline Solids Amorphous Solids
Melting point Melt at fixed temperature
Melt steadily over range of
temperatures
Arrangements of
constituent particles
regular Irregular
Shape Regular and definite shape Irregular shape in nature
Cleavage
When cut, two smooth and
plain pieces are obtained
When cut, two surfaces of
irregular shape is obtained
Heat of fusion definite Indefinite
Anisotropy Anisotropic Isotropic
Nature True solids Pseudo solids

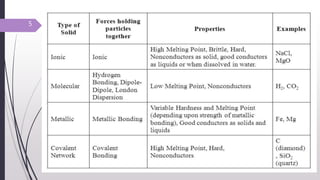
Solid state
1. In a solid, the particles (atoms, molecules or ions) are closely packed
together.
2. The forces between the particles are strong so that the particles cannot eely
but can only vibrate.
3. Thus a solid has a stable, definite shape and a definite volume. Their shape
can be changed only by application of force.
TYPES OF SOLIDS:
1. Following are the different types of solids:
Crystalline solids : It exists as small crystals, each crystal having a
characteristic geometrical shape, in a crystal, the atoms, molecules or ions. are
arranged in a regular repeating three dimensional pattern called the crystal
lattice.
4

Solid state
Amorphous solids :
 It has atoms, molecules or ions arranged at random and lacks the ordered
crystalline lattice.
 In their disordered structure, amorphous solids resemble liquids.
 Crystalline substances are said to be anisotropic (i.e. the magnitude of
physical property varies with directions) whereas amorphous solids are said
to be isotropic (i.e. the magnitude of physical property remains the same in
all directions).
6

Solid state
Depending upon the nature of forces acting the solids can be divided into four
types:
(i) Covalent Solids: In these solids the constituent units are attached by
covalent linkages. Depending on arrangement, these can be divided into
isotropic and anisotropic substances.
Isotropic Substances:
These systems show uniform velocity of light in all directions.
Amorphous substance exhibit this property.
Other parameters like refractive index, thermal and electrical conductivities are
also uniform in all directions.
Eg : Water, glass
7

Solid state
Anisotropic Substances:
 The velocity of light is not uniform in all directions.
 When a ray enters anisotropic substance it splits up into two separate
components which travel with different velocities.
 The other physical properties which are mentioned in isotropic substance also
vary in anisotropic substances.
 Eg: Silver iodide.
8

PROPERTIES OF Crystals:
Crystal habit: The external shape of the crystal is called as the crystal habit.
The plane surfaces of the crystal are called faces and angles between the faces
are called interfacial angles. The interfacial angles for a given crystalline
substance are always the same.
Crystal symmetry: This is an important property of crystals. There are three
types of symmetry elements associated with a crystal. These are called
elements of symmetry.
9

 Plane of symmetry: A crystal is said to have plane of symmetry if it can be
divided by an imaginary line into equal parts, each of which is exact mirror
image of the other.
 Axis of symmetry: It is an imaginary line drawn through the crystal such
that during rotation of crystal through 360°,the crystal looks the same more
than once.
 Centre of symmetry : It is a point at the centre of the crystal so that any
line drawn through it will meet the surface or the crystal at equal distance
on either side.
10

Crystal structure: The particles (atoms, molecules or ions) in crystals are
highly ordered and they are arranged in a regular pattern that extend in all
directions. The overall arrangement of particles in a crystal is called the crystal
lattice, space lattice or lattice.
11

Methods of crystal analysis
 When a beam of X-rays is allowed to pass through crystal lattice, a large
number of images of different intensities are formed.
 A crystal lattice is considered to be made up of regular planes which are
separated by equal distance.
 Since the wavelength of X-ray is comparable to the interatomic distances,
Laue suggested that crystal can act as grating to X-rays.
 So, if the diffracted waves are in the same phase, they reinforce each other
and a series of bright spots are produced on a photographic plate placed in
their path as shown in Fig.
15

Methods of crystal analysis
 On the other hand, if the diffracted waves are out of phase, interference will
result, and dark spots are caused on the photographic plate.
 From the overall diffraction patterns produced by a crystal, we can get the
detailed information regarding the position of particles in the crystal.
16

Bragg's equation
 In 1913 W.L. Bragg made a successful attempt in determining the
interatomic distance in a crystal lattice using X-rays. The study of crystal
structure with the help of X-rays is called X-ray crystallography.
 He showed that:
 X-rays obey laws of reflection
 The extra distance travelled by the second ray [P] is an integral number of
wavelength
𝒏𝝀 = 𝟐𝒅 𝒔𝒊𝒏𝜽
17

Bragg's equation
𝑛λ=2𝑑 𝑠𝑖𝑛𝜃
 For a given set of lattice planes d and A are fixed.
 d - distance between
 λ - wavelength of x-rays
 θ - Angle at which the X-rays strike the crystal
 n - order of reflection.
18

Deviation of Bragg's equation
 As shown in figure a beam of X-ray is following on the crystal surface.
 The 2 successive planes of crystal separated by distance, d.
 Let X-ray of wavelength λ strike the force first plane at an angle θ same rays
are reflected at the same plane. And some will penetrate and get reflected
from the second plane.
 These rays will be in force with those reflected from first plane. If extra
distance (CB+BD) travelled by them is equal to integral no. n of the
wavelengths.
 i.e. n λ = CB+BD -----------(1)
19

Deviation of Bragg's equation
From the geometry we know that
CB = BD = AB sin θ ---------(2)
From (1) and (2)
𝑛λ=2AB 𝑠𝑖𝑛𝜃
𝑛λ=2𝑑 𝑠𝑖𝑛𝜃
This is known as Bragg’s Equation
20

Measurement of diffraction angle θ
1. Rotating crystal method (Bragg 1913)
2. The powder method ( Debye & Scherrer 1916)
21

Rotating crystal method
 A beam of x-rays of known λ falls on a face of the crystal
mounted on a graduated turn table.
 The diffracted rays pass into the ionisation chamber of the
recorder.
 Here they ionise the air and a current flows between the chamber
wall and the electrode inserted in it which is connected to an
electrometer.
 The electrometer reading is proportional to the intensity of x-
rays
23

Rotating crystal method
 As the recorder along with the crystal is rotated, the angles of
maximum intensity are noted on the scale.
 Thus values of θ for n= 1,2,3 etc are used to calculate the
distance d between the lattice planes parallel to the face of the
crystal
24

The powder method
 In this method, the crystalline material contained in a capillary tube is
placed in the camera containing a film strip
 The sample is rotated by means of a motor
 The x-rays passes through the gap between the ends of the film.
 The powdered sample contains small crystals arranged in all
orientations.
 Some will reflect x-rays from each lattice plane at sometimes.
 The reflected X-rays make an angle of 2 θ with the incident X-ray.
 From the geometry of camera, θ can be calculated for different crystal
planes.
25

�ݺ�ߣ

Solid State.pptx

More Related Content

Solid State.pptx