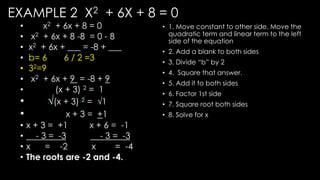Solving Quadratic-Equation.pptx
- 2. ŌĆó Dear God, ŌĆó we humbly gather together virtually. ŌĆó Thinking of starting today's online class. ŌĆó Oh, father, we come to you asking for your guidance, wisdom, and support as we wait to be pumped with knowledge by our teachers. ŌĆó Please help us understand whatever we are being taught, so we can have a brighter future when we finish our program. ŌĆó We pray this trusting your holy name. ŌĆó Amen.
- 3. REMINDERS 2.Always turn on your camera. 1.Be on time. 3.Unmute your audio when called by your teacher. 4.Do have your module, notebook and pen. 6.Be attentive and enjoy learning. 5.Questions will be entertained after a discussed topic.
- 4. ATTENDANCE
- 5. WEEKLY TASK SEPT. 3, 2022 (Saturday) Ō¢║Answer the Pretest Item # 1-5 on pp. 1-2 of your Module
- 6. MATH 9- QUARTER 1 - WEEK 1 QUADRATIC EQUATIONS
- 7. PIC -a- QUAD
- 9. Factoring
- 12. REVIEW: DEFINITIONS: A quadratic equation in one variable is a mathematical sentence of degree 2 that can be written in the standard form ax2 + bx + c = 0, where ØæÄ,ØæÅ, and ØæÉ are real numbers and a ŌēĀ 0. The values of ØæÄ,ØæÅ, and ØæÉ are the numerical coefficients of quadratic term, linear term, and constant term, respectively. ax2 + bx + c = 0 Constant term Linear term Quadratic term
- 13. LESSON 2: SOLVING QUADRATIC EQUATIONS The solution set or roots of quadratic equations are values of the variable that will satisfy the equation.
- 14. METHODS USED TO SOLVE QUADRATIC EQUATIONS 1. Extracting Square Roots 2. Factoring 3. Completing the Square 4. Quadratic Formula
- 15. 1. EXTRACTING SQUARE ROOTS/SQUARE ROOT PROPERTY ŌĆó
- 16. Example 1 x2 ŌĆō 100 = 0 x = ┬▒ 10 3x2 + 15 = 0 x2 ŌĆō 100 + 100 = 0 + 100 x2 = 100 Solution Set: {10, -10} Example 5 Example 4 Example 3 Example 2 x2 = 0 x = 0 Solution Set: {0} 3x2 + 15 (-15) = 0 + (-15) 3x2 = -15 x2 = -5 Solution Set: No Solution 2x2 - 6 = 0 2x2 = 6 x2 = 3 (x ŌĆō 5)2 = 16 x - 5 = ┬▒4 x ŌĆō 5 + 5=┬▒4 +5 x = 5 ┬▒ 4 Solution Set: {9, 1} x = 5 + 4 x = 9 x = 1 x = 5 - 4
- 17. 2. FACTORING Factoring is typically one of the easiest and quickest ways to solve quadratic equations; however, Not all quadratic polynomials can be factored. Applicable whenever the polynomial in the equation is factorable. This means that factoring will not work to solve many quadratic equations.
- 18. EXAMPLE 1: STEPS Solve: ؤæØÆÖ 2 ŌłÆ ؤÅؤōØÆÖ = Ø¤Ä Ø¤æØÆÖ(ØÆÖ ŌĆō 5) = Ø¤Ä Ø¤æØÆÖ = 0 ØÆÖ = 0 ØÆÖ ŌĆō 5 = 0 ØÆÖ = 5 or The roots are 0 and 5. Transform the equation in standard form if necessary Factor the Polynomial Apply the Zero Product Property by setting each factor equal to zero Solve the equation ؤæ ؤæ
- 19. EXAMPLE 2: STEPS Solve: ØÆÖ 2 = 9ØÆÖ - 18 ØÆÖ 2 ŌĆō 9x + 18 = 9x ŌĆō 9x -18 + 18 ØÆÖ - 6 = 0 ØÆÖ = 6 ØÆÖ ŌĆō 3 = 0 ØÆÖ = 3 or The roots are 6 and Transform the equation in standard form if necessary Write the equation in Standard Form by adding -9x and 18 on both sides. Apply the Zero Product Property by setting each factor equal to zero Solve the equation Simplify by combining like terms. Øæź 2 ŌłÆ 9Øæź + 18 = 0 (Øæź ŌĆō 6) (Øæź ŌĆō 3) = 0 Factor the Polynomial.
- 20. 3. COMPLETING THE SQUARE This method will work to solve ALL quadratic equations; however, it is ŌĆ£messyŌĆØ to solve quadratic equations by completing the square if a ŌēĀ 1 and/or b is an odd number. Completing the square is a great choice for solving quadratic equations if a = 1 and b is an even number.
- 21. 3. COMPLETING THE SQUARE Before we use this method for solving quadratic equation, let us recall that if the expression ØæÄØæź2 + ØæÅØæź + ØæÉ is a perfect square trinomial, it can be factored out into two identical binomial factors. Øæź 2 + 4Øæź + 4 Øæź 2 - 10Øæź + 25 4Øæź 2 + 12Øæź + 9 = (Øæź + 2)(Øæź + 2) = (Øæź + 2) 2 = (2Øæź + 3) 2 = (Øæź - 5) 2 = (Øæź - 5)(Øæź - 5) = (2Øæź + 3)(2Øæź + 3)
- 22. EXAMPLE 1 X2 + 12X = 0 ŌĆó x2 + 12x = 0 ŌĆó ŌĆó x2 + 12x + ___ = 0 + ___ ŌĆó b= 12 12 / 2 =6 ŌĆó 62=36 ŌĆó x2 + 12x + 36 = 0 + 36 ŌĆó (x + 6) 2 = 36 ŌĆó ŌłÜ(x + 6) 2 = ŌłÜ36 ŌĆó x + 6 = +6 ŌĆó x + 6 = +6 x + 6 = -6 ŌĆó -6 = -6 - 6 = -6 ŌĆó x = 0 x = -12 ŌĆó The roots are 0 and -12. ŌĆó 1. Make one side a perfect square. Move the quadratic term and linear term to the left side of the equation ŌĆó 2. Add a blank to both sides ŌĆó 3. Divide ŌĆ£bŌĆØ by 2 ŌĆó 4. Square that answer. ŌĆó 5. Add it to both sides ŌĆó 6. Factor 1st side ŌĆó 7. Square root both sides ŌĆó 8. Solve for x
- 23. EXAMPLE 2 X2 + 6X + 8 = 0 ŌĆó x2 + 6x + 8 = 0 ŌĆó x2 + 6x + 8 -8 = 0 - 8 ŌĆó x2 + 6x + ___ = -8 + ___ ŌĆó b= 6 6 / 2 =3 ŌĆó 32=9 ŌĆó x2 + 6x + 9 = -8 + 9 ŌĆó (x + 3) 2 = 1 ŌĆó ŌłÜ(x + 3) 2 = ŌłÜ1 ŌĆó x + 3 = +1 ŌĆó x + 3 = +1 x + 6 = -1 ŌĆó - 3 = -3 - 3 = -3 ŌĆó x = -2 x = -4 ŌĆó The roots are -2 and -4. ŌĆó 1. Move constant to other side. Move the quadratic term and linear term to the left side of the equation ŌĆó 2. Add a blank to both sides ŌĆó 3. Divide ŌĆ£bŌĆØ by 2 ŌĆó 4. Square that answer. ŌĆó 5. Add it to both sides ŌĆó 6. Factor 1st side ŌĆó 7. Square root both sides ŌĆó 8. Solve for x
- 24. 4. QUADRATIC FORMULA This method will work to solve ALL quadratic equations; however, for many equations it takes longer than some of the methods discussed earlier. The quadratic formula is a good choice if the quadratic polynomial cannot be factored, the equation cannot be written as (x+c)2 = n, or a is not 1 and/or b is an odd number.
- 25. Solve using the Quadratic Formula. 1.) x2 = x + 20 1x2 + (ŌĆō1x) + (ŌĆō20) = 0 a=1 b=-1 c=-20 Write in standard form. Identify a, b, and c. Use the quadratic formula. Simplify. Substitute 1 for a, ŌĆō1 for b, and ŌĆō20 for c.
- 26. Solve using the Quadratic Formula. x = 5 or x = ŌĆō4 Simplify. Write as two equations. Solve each equation. x2 = x + 20
- 27. Solve using the Quadratic Formula. 2.) ŌĆō3x2 + 5x + 2 = 0 Identify a, b, and c. Use the Quadratic Formula. Substitute ŌĆō3 for a, 5 for b, and 2 for c. Simplify. ŌĆō3x2 + 5x + 2 = 0 a=-3 b=5 c=2
- 28. Solve using the Quadratic Formula. Simplify. Write as two equations. Solve each equation. x = ŌĆō or x = 2 ŌĆō3x2 + 5x + 2 = 0
- 29. Solve using the Quadratic Formula. 3.) 2 ŌĆō 5x2 = ŌĆō9x Write in standard form. Identify a, b, and c. (ŌĆō5)x2 + 9x + (2) = 0 a=-5 b=9 c=2 Use the Quadratic Formula. Substitute ŌĆō5 for a, 9 for b, and 2 for c. Simplify.
- 30. Method Most appropriate to use Extracting Square Roots or Square- Root Property for quadratic equations of the form Øæź2 = Øæś Factoring If the constant term is 0, or if ØæÄØæź2 + ØæÅØæź + ØæÉ is factorable. Completing the square For any quadratic equation of the form ØæÄØæź2 + ØæÅØæź + ØæÉ, where a is 1 and b is even. Quadratic formula For any quadratic equation. REMEMBER
- 31. EXERCISES: SOLVE THE FOLLOWING USING THE APPROPRIATE METHOD OF SOLVING QUADRATIC EQUATIONS. 1. 2. 3. 4. 5. 2x2 ŌĆō 2x + 3 = 0 x2 + 8x - 84 = 0 x2 = 121 x2 - 4x - 5 = 0 2x2 = ŌĆō 5x + 10