–Ь–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–∞—П —А–µ–≥—А–µ—Б—Б–Є—П
- 1. –Ю—Б–љ–Њ–≤–љ–∞—П —Ж–µ–ї—М –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є вАУ –њ–Њ—Б—В—А–Њ–Є—В—М –Љ–Њ–і–µ–ї—М —Б –±–Њ–ї—М—И–Є–Љ —З–Є—Б–ї–Њ–Љ —Д–∞–Ї—В–Њ—А–Њ–≤, –Њ–њ—А–µ–і–µ–ї–Є–≤ –њ—А–Є —Н—В–Њ–Љ –≤–ї–Є—П–љ–Є–µ –Ї–∞–ґ–і–Њ–≥–Њ –Є–Ј –љ–Є—Е –≤ –Њ—В–і–µ–ї—М–љ–Њ—Б—В–Є, –∞ —В–∞–Ї–ґ–µ —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ–µ –Є—Е –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–µ –љ–∞ –Љ–Њ–і–µ–ї–Є—А—Г–µ–Љ—Л–є –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М.
- 2. пБљ —Б–њ–µ—Ж–Є—Д–Є–Ї–∞—Ж–Є–Є –Љ–Њ–і–µ–ї–Є: –Њ—В–±–Њ—А —Д–∞–Ї—В–Њ—А–Њ–≤ –Є –≤—Л–±–Њ—А –≤–Є–і–∞ —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є. пБљ –§–∞–Ї—В–Њ—А—Л, –≤–Ї–ї—О—З–∞–µ–Љ—Л–µ –≤–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ—Г—О —А–µ–≥—А–µ—Б—Б–Є—О, –і–Њ–ї–ґ–љ—Л –Њ—В–≤–µ—З–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ —В—А–µ–±–Њ–≤–∞–љ–Є—П–Љ: 1. –Ю–љ–Є –і–Њ–ї–ґ–љ—Л –±—Л—В—М –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ–љ–љ–Њ –Є–Ј–Љ–µ—А–Є–Љ—Л. –Х—Б–ї–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –≤–Ї–ї—О—З–Є—В—М –≤ –Љ–Њ–і–µ–ї—М –Ї–∞—З–µ—Б—В–≤–µ–љ–љ—Л–є —Д–∞–Ї—В–Њ—А, –љ–µ –Є–Љ–µ—О—Й–Є–є –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П, —В–Њ –µ–Љ—Г –љ—Г–ґ–љ–Њ –њ—А–Є–і–∞—В—М –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ–љ–љ—Г—О –Њ–њ—А–µ–і–µ–ї–µ–љ–љ–Њ—Б—В—М. пБљ 2. –§–∞–Ї—В–Њ—А—Л –љ–µ –і–Њ–ї–ґ–љ—Л –±—Л—В—М –Є–љ—В–µ—А–Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ—Л –Є —В–µ–Љ –±–Њ–ї–µ–µ –љ–∞—Е–Њ–і–Є—В—М—Б—П –≤ —В–Њ—З–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї—М–љ–Њ–є —Б–≤—П–Ј–Є
- 3. пБљ –Т–Ї–ї—О—З–µ–љ–Є–µ –≤ –Љ–Њ–і–µ–ї—М —Д–∞–Ї—В–Њ—А–Њ–≤ —Б –≤—Л—Б–Њ–Ї–Њ–є –Є–љ—В–µ—А–Ї–Њ—А—А–µ–ї—П—Ж–Є–µ–є (—В.–µ. –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Љ–µ–ґ–і—Г –Њ–±—К—П—Б–љ—П—О—Й–Є–Љ–Є –њ–µ—А–µ–Љ–µ–љ–љ—Л–Љ–Є), –Љ–Њ–ґ–µ—В –њ—А–Є–≤–µ—Б—В–Є –Ї –љ–µ–ґ–µ–ї–∞—В–µ–ї—М–љ—Л–Љ –њ–Њ—Б–ї–µ–і—Б—В–≤–Є—П–Љ вАУ —Б–Є—Б—В–µ–Љ–∞ –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –Љ–Њ–ґ–µ—В –Њ–Ї–∞–Ј–∞—В—М—Б—П –њ–ї–Њ—Е–Њ –Њ–±—Г—Б–ї–Њ–≤–ї–µ–љ–љ–Њ–є –Є –њ–Њ–≤–ї–µ—З—М –Ј–∞ —Б–Њ–±–Њ–є –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В—М –Є –љ–µ–љ–∞–і–µ–ґ–љ–Њ—Б—В—М –Њ—Ж–µ–љ–Њ–Ї –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —А–µ–≥—А–µ—Б—Б–Є–Є. пБљ –Х—Б–ї–Є –Љ–µ–ґ–і—Г —Д–∞–Ї—В–Њ—А–∞–Љ–Є —Б—Г—Й–µ—Б—В–≤—Г–µ—В –≤—Л—Б–Њ–Ї–∞—П –Ї–Њ—А—А–µ–ї—П—Ж–Є—П, —В–Њ –љ–µ–ї—М–Ј—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –Є—Е –Є–Ј–Њ–ї–Є—А–Њ–≤–∞–љ–љ–Њ–µ –≤–ї–Є—П–љ–Є–µ –љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ—Л–є –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М –Є –њ–∞—А–∞–Љ–µ—В—А—Л —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є –Њ–Ї–∞–Ј—Л–≤–∞—О—В—Б—П –љ–µ–Є–љ—В–µ—А–њ—А–µ—В–Є—А—Г–µ–Љ—Л–Љ–Є. пБљ –Т–Ї–ї—О—З–∞–µ–Љ—Л–µ –≤–Њ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ—Г—О —А–µ–≥—А–µ—Б—Б–Є—О —Д–∞–Ї—В–Њ—А—Л –і–Њ–ї–ґ–љ—Л –Њ–±—К—П—Б–љ–Є—В—М –≤–∞—А–Є–∞—Ж–Є—О –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ–є –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є
- 4. пБљ –Х—Б–ї–Є —Б—В—А–Њ–Є—В—Б—П –Љ–Њ–і–µ–ї—М —Б –љ–∞–±–Њ—А–Њ–Љ m —Д–∞–Ї—В–Њ—А–Њ–≤, —В–Њ –і–ї—П –љ–µ–µ —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ—В—Б—П –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М –і–µ—В–µ—А–Љ–Є–љ–∞—Ж–Є–Є , –Ї–Њ—В–Њ—А—Л–є —Д–Є–Ї—Б–Є—А—Г–µ—В –і–Њ–ї—О –Њ–±—К—П—Б–љ–µ–љ–љ–Њ–є –≤–∞—А–Є–∞—Ж–Є–Є —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ–Њ–≥–Њ –њ—А–Є–Ј–љ–∞–Ї–∞ –Ј–∞ —Б—З–µ—В —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л—Е –≤ —А–µ–≥—А–µ—Б—Б–Є–Є —Д–∞–Ї—В–Њ—А–Њ–≤. –Т–ї–Є—П–љ–Є–µ –і—А—Г–≥–Є—Е, –љ–µ —Г—З—В–µ–љ–љ—Л—Е –≤ –Љ–Њ–і–µ–ї–Є —Д–∞–Ї—В–Њ—А–Њ–≤, –Њ—Ж–µ–љ–Є–≤–∞–µ—В—Б—П –Ї–∞–Ї —Б —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–є –Њ—Б—В–∞—В–Њ—З–љ–Њ–є –і–Є—Б–њ–µ—А—Б–Є–µ–є . пБљ –Я—А–Є –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ–Њ–Љ –≤–Ї–ї—О—З–µ–љ–Є–Є –≤ —А–µ–≥—А–µ—Б—Б–Є—О m —Д–∞–Ї—В–Њ—А–∞ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –і–µ—В–µ—А–Љ–Є–љ–∞—Ж–Є–Є –і–Њ–ї–ґ–µ–љ –≤–Њ–Ј—А–∞—Б—В–∞—В—М, –∞ –Њ—Б—В–∞—В–Њ—З–љ–∞—П –і–Є—Б–њ–µ—А—Б–Є—П —Г–Љ–µ–љ—М—И–∞—В—М—Б—П: пБљ –Є . пБљ –Х—Б–ї–Є –ґ–µ —Н—В–Њ–≥–Њ –љ–µ –њ—А–Њ–Є—Б—Е–Њ–і–Є—В –Є –і–∞–љ–љ—Л–µ –њ–Њ–Ї–∞–Ј–∞—В–µ–ї–Є –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –љ–µ –Њ—В–ї–Є—З–∞—О—В—Б—П –і—А—Г–≥ –Њ—В –і—А—Г–≥–∞, —В–Њ –≤–Ї–ї—О—З–∞–µ–Љ—Л–є –≤ –∞–љ–∞–ї–Є–Ј —Д–∞–Ї—В–Њ—А –љ–µ —Г–ї—Г—З—И–∞–µ—В –Љ–Њ–і–µ–ї—М –Є –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є —П–≤–ї—П–µ—В—Б—П –ї–Є—И–љ–Є–Љ —Д–∞–Ї—В–Њ—А–Њ–Љ.
- 5. пБљ –Э–∞—Б—Л—Й–µ–љ–Є–µ –Љ–Њ–і–µ–ї–Є –ї–Є—И–љ–Є–Љ–Є —Д–∞–Ї—В–Њ—А–∞–Љ–Є –љ–µ —Б–љ–Є–ґ–∞–µ—В –≤–µ–ї–Є—З–Є–љ—Г –Њ—Б—В–∞—В–Њ—З–љ–Њ–є –і–Є—Б–њ–µ—А—Б–Є–Є –Є –љ–µ —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М –і–µ—В–µ—А–Љ–Є–љ–∞—Ж–Є–Є –Є –њ—А–Є–≤–Њ–і–Є—В –Ї —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Њ–є –љ–µ–Ј–љ–∞—З–Є–Љ–Њ—Б—В–Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ —А–µ–≥—А–µ—Б—Б–Є–Є –њ–Њ –Ї—А–Є—В–µ—А–Є—О –°—В—М—О–і–µ–љ—В–∞ пБљ –Я–Њ—Н—В–Њ–Љ—Г –Њ—В–±–Њ—А —Д–∞–Ї—В–Њ—А–Њ–≤ –Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П –≤ –і–≤–µ —Б—В–∞–і–Є–Є: –љ–∞ –њ–µ—А–≤–Њ–є –њ–Њ–і–±–Є—А–∞—О—В—Б—П —Д–∞–Ї—В–Њ—А—Л –Є—Б—Е–Њ–і—П –Є–Ј —Б—Г—Й–љ–Њ—Б—В–Є –њ—А–Њ–±–ї–µ–Љ—Л; –љ–∞ –≤—В–Њ—А–Њ–є вАУ –љ–∞ –Њ—Б–љ–Њ–≤–µ –Љ–∞—В—А–Є—Ж—Л –њ–Њ–Ї–∞–Ј–∞—В–µ–ї–µ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Њ–њ—А–µ–і–µ–ї—П—О—В —Б—В–∞—В–Є—Б—В–Є–Ї–Є –і–ї—П –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ —А–µ–≥—А–µ—Б—Б–Є–Є. пБљ –Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Є–љ—В–µ—А–Ї–Њ—А—А–µ–ї—П—Ж–Є–Є (—В.–µ. –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Љ–µ–ґ–і—Г –Њ–±—К—П—Б–љ—П—О—Й–Є–Љ–Є –њ–µ—А–µ–Љ–µ–љ–љ—Л–Љ–Є) –њ–Њ–Ј–≤–Њ–ї—П—О—В –Є—Б–Ї–ї—О—З–∞—В—М –Є–Ј –Љ–Њ–і–µ–ї–Є –і—Г–±–ї–Є—А—Г—О—Й–Є–µ —Д–∞–Ї—В–Њ—А—Л. –°—З–Є—В–∞–µ—В—Б—П, —З—В–Њ –і–≤–µ –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ —П–≤–љ–Њ –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л, —В.–µ. –љ–∞—Е–Њ–і—П—В—Б—П –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є –≤ –ї–Є–љ–µ–є–љ–Њ–є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є, –µ—Б–ї–Є . –Х—Б–ї–Є —Д–∞–Ї—В–Њ—А—Л —П–≤–љ–Њ –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л, —В–Њ –Њ–љ–Є –і—Г–±–ї–Є—А—Г—О—В –і—А—Г–≥ –і—А—Г–≥–∞ –Є –Њ–і–Є–љ –Є–Ј –љ–Є—Е —А–µ–Ї–Њ–Љ–µ–љ–і—Г–µ—В—Б—П –Є—Б–Ї–ї—О—З–Є—В—М –Є–Ј —А–µ–≥—А–µ—Б—Б–Є–Є
- 6. пБљ –Я—Г—Б—В—М, –љ–∞–њ—А–Є–Љ–µ—А, –њ—А–Є –Є–Ј—Г—З–µ–љ–Є–Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Љ–∞—В—А–Є—Ж–∞ –њ–∞—А–љ—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Њ–Ї–∞–Ј–∞–ї–∞—Б—М —Б–ї–µ–і—Г—О—Й–µ–є: –Ю—З–µ–≤–Є–і–љ–Њ, —З—В–Њ —Д–∞–Ї—В–Њ—А—Л —Е1 –Є —Е2 –і—Г–±–ї–Є—А—Г—О—В –і—А—Г–≥ –і—А—Г–≥–∞. –Т –∞–љ–∞–ї–Є–Ј —Ж–µ–ї–µ—Б–Њ–Њ–±—А–∞–Ј–љ–Њ –≤–Ї–ї—О—З–Є—В—М —Д–∞–Ї—В–Њ—А —Е2, –∞ –љ–µ —Е1. –Я–Њ—Н—В–Њ–Љ—Г –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –≤–Ї–ї—О—З–∞—О—В—Б—П —Д–∞–Ї—В–Њ—А—Л —Е2, —Е3.
- 7. пБљ –Я–Њ –≤–µ–ї–Є—З–Є–љ–µ –њ–∞—А–љ—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞–µ—В—Б—П –ї–Є—И—М —П–≤–љ–∞—П –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В—М —Д–∞–Ї—В–Њ—А–Њ–≤. –Э–∞–Є–±–Њ–ї—М—И–Є–µ —В—А—Г–і–љ–Њ—Б—В–Є –≤ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є –∞–њ–њ–∞—А–∞—В–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –≤–Њ–Ј–љ–Є–Ї–∞—О—В –њ—А–Є –љ–∞–ї–Є—З–Є–Є –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В–Є —Д–∞–Ї—В–Њ—А–Њ–≤, –Ї–Њ–≥–і–∞ –±–Њ–ї–µ–µ —З–µ–Љ –і–≤–∞ —Д–∞–Ї—В–Њ—А–∞ —Б–≤—П–Ј–∞–љ—Л –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є –ї–Є–љ–µ–є–љ–Њ–є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М—О, —В.–µ. –Є–Љ–µ–µ—В –Љ–µ—Б—В–Њ —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ–µ –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–µ —Д–∞–Ї—В–Њ—А–Њ–≤ –і—А—Г–≥ –љ–∞ –і—А—Г–≥–∞. –Э–∞–ї–Є—З–Є–µ –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В–Є —Д–∞–Ї—В–Њ—А–Њ–≤ –Љ–Њ–ґ–µ—В –Њ–Ј–љ–∞—З–∞—В—М, —З—В–Њ –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Д–∞–Ї—В–Њ—А—Л –±—Г–і—Г—В –≤—Б–µ–≥–і–∞ –і–µ–є—Б—В–≤–Њ–≤–∞—В—М –≤ —Г–љ–Є—Б–Њ–љ. –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –≤–∞—А–Є–∞—Ж–Є—П –≤ –Є—Б—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е –њ–µ—А–µ—Б—В–∞–µ—В –±—Л—В—М –њ–Њ–ї–љ–Њ—Б—В—М—О –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ–є –Є –љ–µ–ї—М–Ј—П –Њ—Ж–µ–љ–Є—В—М –≤–Њ–Ј–і–µ–є—Б—В–≤–Є–µ –Ї–∞–ґ–і–Њ–≥–Њ —Д–∞–Ї—В–Њ—А–∞ –≤ –Њ—В–і–µ–ї—М–љ–Њ—Б—В–Є.
- 8. пБљ –Т–Ї–ї—О—З–µ–љ–Є–µ –≤ –Љ–Њ–і–µ–ї—М –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л—Е —Д–∞–Ї—В–Њ—А–Њ–≤ –љ–µ–ґ–µ–ї–∞—В–µ–ї—М–љ–Њ –≤ —Б–Є–ї—Г —Б–ї–µ–і—Г—О—Й–Є—Е –њ–Њ—Б–ї–µ–і—Б—В–≤–Є–є: пБљ –Ч–∞—В—А—Г–і–љ—П–µ—В—Б—П –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є—П –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –Ї–∞–Ї —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –і–µ–є—Б—В–≤–Є—П —Д–∞–Ї—В–Њ—А–Њ–≤ –≤ ¬Ђ—З–Є—Б—В–Њ–Љ¬ї –≤–Є–і–µ, –Є–±–Њ —Д–∞–Ї—В–Њ—А—Л –Ї–Њ—А—А–µ–ї–Є—А–Њ–≤–∞–љ—Л; –њ–∞—А–∞–Љ–µ—В—А—Л –ї–Є–љ–µ–є–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є —В–µ—А—П—О—В —Н–Ї–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї. пБљ –Ю—Ж–µ–љ–Ї–Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –љ–µ–љ–∞–і–µ–ґ–љ—Л, –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞—О—В –±–Њ–ї—М—И–Є–µ —Б—В–∞–љ–і–∞—А—В–љ—Л–µ –Њ—И–Є–±–Ї–Є –Є –Љ–µ–љ—П—О—В—Б—П —Б –Є–Ј–Љ–µ–љ–µ–љ–Є–µ–Љ –Њ–±—К–µ–Љ–∞ –љ–∞–±–ї—О–і–µ–љ–Є–є (–љ–µ —В–Њ–ї—М–Ї–Њ –њ–Њ –≤–µ–ї–Є—З–Є–љ–µ, –љ–Њ –Є –њ–Њ –Ј–љ–∞–Ї—Г), —З—В–Њ –і–µ–ї–∞–µ—В –Љ–Њ–і–µ–ї—М –љ–µ–њ—А–Є–≥–Њ–і–љ–Њ–є –і–ї—П –∞–љ–∞–ї–Є–Ј–∞ –Є –њ—А–Њ–≥–љ–Њ–Ј–Є—А–Њ–≤–∞–љ–Є—П. пБљ –Ф–ї—П –Њ—Ж–µ–љ–Ї–Є –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В–Є —Д–∞–Ї—В–Њ—А–Њ–≤ –Љ–Њ–ґ–µ—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –Љ–∞—В—А–Є—Ж—Л –њ–∞—А–љ—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Љ–µ–ґ–і—Г —Д–∞–Ї—В–Њ—А–∞–Љ–Є.
- 10. пБљ –І–µ–Љ –±–ї–Є–ґ–µ –Ї –љ—Г–ї—О –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –Љ–∞—В—А–Є—Ж—Л –Љ–µ–ґ—Д–∞–Ї—В–Њ—А–љ–Њ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є, —В–µ–Љ —Б–Є–ї—М–љ–µ–µ –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В—М —Д–∞–Ї—В–Њ—А–Њ–≤ –Є –љ–µ–љ–∞–і–µ–ґ–љ–µ–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є. –Ш, –љ–∞–Њ–±–Њ—А–Њ—В, —З–µ–Љ –±–ї–Є–ґ–µ –Ї –µ–і–Є–љ–Є—Ж–µ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –Љ–∞—В—А–Є—Ж—Л –Љ–µ–ґ—Д–∞–Ї—В–Њ—А–љ–Њ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є, —В–µ–Љ –Љ–µ–љ—М—И–µ –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В—М —Д–∞–Ї—В–Њ—А–Њ–≤. пБљ –°—Г—Й–µ—Б—В–≤—Г–µ—В —А—П–і –њ–Њ–і—Е–Њ–і–Њ–≤ –њ—А–µ–Њ–і–Њ–ї–µ–љ–Є—П —Б–Є–ї—М–љ–Њ–є –Љ–µ–ґ—Д–∞–Ї—В–Њ—А–љ–Њ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є. –°–∞–Љ—Л–є –њ—А–Њ—Б—В–Њ–є –њ—Г—В—М —Г—Б—В—А–∞–љ–µ–љ–Є—П –Љ—Г–ї—М—В–Є–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ–Њ—Б—В–Є —Б–Њ—Б—В–Њ–Є—В –≤ –Є—Б–Ї–ї—О—З–µ–љ–Є–Є –Є–Ј –Љ–Њ–і–µ–ї–Є –Њ–і–љ–Њ–≥–Њ –Є–ї–Є –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е —Д–∞–Ї—В–Њ—А–Њ–≤. –Ф—А—Г–≥–Њ–є –њ–Њ–і—Е–Њ–і —Б–≤—П–Ј–∞–љ —Б –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ–Љ —Д–∞–Ї—В–Њ—А–Њ–≤, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ —Г–Љ–µ–љ—М—И–∞–µ—В—Б—П –Ї–Њ—А—А–µ–ї—П—Ж–Є—П –Љ–µ–ґ–і—Г –љ–Є–Љ–Є.
- 11. пБљ –Ю–і–љ–Є–Љ –Є–Ј –њ—Г—В–µ–є —Г—З–µ—В–∞ –≤–љ—Г—В—А–µ–љ–љ–µ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є —Д–∞–Ї—В–Њ—А–Њ–≤ —П–≤–ї—П–µ—В—Б—П –њ–µ—А–µ—Е–Њ–і –Ї —Б–Њ–≤–Љ–µ—Й–µ–љ–љ—Л–Љ —Г—А–∞–≤–љ–µ–љ–Є—П–Љ —А–µ–≥—А–µ—Б—Б–Є–Є, —В.–µ. –Ї —Г—А–∞–≤–љ–µ–љ–Є—П–Љ, –Ї–Њ—В–Њ—А—Л–µ –Њ—В—А–∞–ґ–∞—О—В –љ–µ —В–Њ–ї—М–Ї–Њ –≤–ї–Є—П–љ–Є–µ —Д–∞–Ї—В–Њ—А–Њ–≤, –љ–Њ –Є –Є—Е –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є–µ. –Ґ–∞–Ї, –µ—Б–ї–Є , —В–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —Б–Њ–≤–Љ–µ—Й–µ–љ–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П: пБљ –†–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –≤–Ї–ї—О—З–∞–µ—В –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є–µ –њ–µ—А–≤–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ (–≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є–µ –і–≤—Г—Е —Д–∞–Ї—В–Њ—А–Њ–≤). –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ –≤–Ї–ї—О—З–µ–љ–Є–µ –≤ –Љ–Њ–і–µ–ї—М –Є –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є–є –±–Њ–ї–µ–µ –≤—Л—Б–Њ–Ї–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞, –µ—Б–ї–Є –±—Г–і–µ—В –і–Њ–Ї–∞–Ј–∞–љ–∞ –Є—Е —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–∞—П –Ј–љ–∞—З–Є–Љ–Њ—Б—В—М –њ–Њ F- –Ї—А–Є—В–µ—А–Є—О –§–Є—И–µ—А–∞
- 12. пБљ –Ю—В–±–Њ—А —Д–∞–Ї—В–Њ—А–Њ–≤, –≤–Ї–ї—О—З–∞–µ–Љ—Л—Е –≤ —А–µ–≥—А–µ—Б—Б–Є—О, —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Є–Љ –Є–Ј –≤–∞–ґ–љ–µ–є—И–Є—Е —Н—В–∞–њ–Њ–≤ –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П –Љ–µ—В–Њ–і–Њ–≤ —А–µ–≥—А–µ—Б—Б–Є–Є. –Я–Њ–і—Е–Њ–і—Л –Ї –Њ—В–±–Њ—А—Г —Д–∞–Ї—В–Њ—А–Њ–≤ –љ–∞ –Њ—Б–љ–Њ–≤–µ –њ–Њ–Ї–∞–Ј–∞—В–µ–ї–µ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є –Љ–Њ–≥—Г—В –±—Л—В—М —А–∞–Ј–љ—Л–µ. –Ю–љ–Є –њ—А–Є–≤–Њ–і—П—В –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Ї —А–∞–Ј–љ—Л–Љ –Љ–µ—В–Њ–і–Є–Ї–∞–Љ. –Т –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В —В–Њ–≥–Њ, –Ї–∞–Ї–∞—П –Љ–µ—В–Њ–і–Є–Ї–∞ –њ–Њ—Б—В—А–Њ–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є –њ—А–Є–љ—П—В–∞, –Љ–µ–љ—П–µ—В—Б—П –∞–ї–≥–Њ—А–Є—В–Љ –µ–µ —А–µ—И–µ–љ–Є—П –љ–∞ –≠–Т–Ь. пБљ –Э–∞–Є–±–Њ–ї–µ–µ —И–Є—А–Њ–Ї–Њ–µ –њ—А–Є–Љ–µ–љ–µ–љ–Є–µ –њ–Њ–ї—Г—З–Є–ї–Є —Б–ї–µ–і—Г—О—Й–Є–µ –Љ–µ—В–Њ–і—Л –њ–Њ—Б—В—А–Њ–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є: пБљ –Ь–µ—В–Њ–і –Є—Б–Ї–ї—О—З–µ–љ–Є—П вАУ –Њ—В—Б–µ–≤ —Д–∞–Ї—В–Њ—А–Њ–≤ –Є–Ј –њ–Њ–ї–љ–Њ–≥–Њ –µ–≥–Њ –љ–∞–±–Њ—А–∞. пБљ –Ь–µ—В–Њ–і –≤–Ї–ї—О—З–µ–љ–Є—П вАУ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ–Њ–µ –≤–≤–µ–і–µ–љ–Є–µ —Д–∞–Ї—В–Њ—А–∞. пБљ –®–∞–≥–Њ–≤—Л–є —А–µ–≥—А–µ—Б—Б–Є–Њ–љ–љ—Л–є –∞–љ–∞–ї–Є–Ј вАУ –Є—Б–Ї–ї—О—З–µ–љ–Є–µ —А–∞–љ–µ–µ –≤–≤–µ–і–µ–љ–љ–Њ–≥–Њ —Д–∞–Ї—В–Њ—А–∞. пБљ –Я—А–Є –Њ—В–±–Њ—А–µ —Д–∞–Ї—В–Њ—А–Њ–≤ —В–∞–Ї–ґ–µ —А–µ–Ї–Њ–Љ–µ–љ–і—Г–µ—В—Б—П –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –њ—А–∞–≤–Є–ї–Њ–Љ: —З–Є—Б–ї–Њ –≤–Ї–ї—О—З–∞–µ–Љ—Л—Е —Д–∞–Ї—В–Њ—А–Њ–≤ –Њ–±—Л—З–љ–Њ –≤ 6вАУ7 —А–∞–Ј –Љ–µ–љ—М—И–µ –Њ–±—К–µ–Љ–∞ —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В–Є, –њ–Њ –Ї–Њ—В–Њ—А–Њ–є —Б—В—А–Њ–Є—В—Б—П —А–µ–≥—А–µ—Б—Б–Є—П. –Х—Б–ї–Є —Н—В–Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–∞—А—Г—И–µ–љ–Њ, —В–Њ —З–Є—Б–ї–Њ —Б—В–µ–њ–µ–љ–µ–є —Б–≤–Њ–±–Њ–і—Л –Њ—Б—В–∞—В–Њ—З–љ–Њ–є –і–Є—Б–њ–µ—А—Б–Є–Є –Њ—З–µ–љ—М –Љ–∞–ї–Њ. –≠—В–Њ –њ—А–Є–≤–Њ–і–Є—В –Ї —В–Њ–Љ—Г, —З—В–Њ –њ–∞—А–∞–Љ–µ—В—А—Л —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є –Њ–Ї–∞–Ј—Л–≤–∞—О—В—Б—П —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є –љ–µ–Ј–љ–∞—З–Є–Љ—Л–Љ–Є, –∞ -–Ї—А–Є—В–µ—А–Є–є –Љ–µ–љ—М—И–µ —В–∞–±–ї–Є—З–љ–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П.
- 13. пБљ –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –ї–Є–љ–µ–є–љ—Г—О –Љ–Њ–і–µ–ї—М –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є (2.1) пБљ –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–є –њ–Њ–і—Е–Њ–і –Ї –Њ—Ж–µ–љ–Є–≤–∞–љ–Є—О –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –ї–Є–љ–µ–є–љ–Њ–є –Љ–Њ–і–µ–ї–Є –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –Њ—Б–љ–Њ–≤–∞–љ –љ–∞ –Љ–µ—В–Њ–і–µ –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ (–Ь–Э–Ъ). –Ь–Э–Ъ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –њ–Њ–ї—Г—З–Є—В—М —В–∞–Ї–Є–µ –Њ—Ж–µ–љ–Ї–Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤, –њ—А–Є –Ї–Њ—В–Њ—А—Л—Е —Б—Г–Љ–Љ–∞ –Ї–≤–∞–і—А–∞—В–Њ–≤ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–є —Д–∞–Ї—В–Є—З–µ—Б–Ї–Є—Е –Ј–љ–∞—З–µ–љ–Є–є —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ–Њ–≥–Њ –њ—А–Є–Ј–љ–∞–Ї–∞ –Њ—В —А–∞—Б—З–µ—В–љ—Л—Е –Љ–Є–љ–Є–Љ–∞–ї—М–љ–∞: (2.2)
- 14. пБљ –Ъ–∞–Ї –Є–Ј–≤–µ—Б—В–љ–Њ –Є–Ј –Ї—Г—А—Б–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞, –і–ї—П —В–Њ–≥–Њ —З—В–Њ–±—Л –љ–∞–є—В–Є —Н–Ї—Б—В—А–µ–Љ—Г–Љ —Д—Г–љ–Ї—Ж–Є–Є –љ–µ—Б–Ї–Њ–ї—М–Ї–Є—Е –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е, –љ–∞–і–Њ –≤—Л—З–Є—Б–ї–Є—В—М —З–∞—Б—В–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–µ—А–≤–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –њ–Њ –Ї–∞–ґ–і–Њ–Љ—Г –Є–Ј –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Є –њ—А–Є—А–∞–≤–љ—П—В—М –Є—Е –Ї –љ—Г–ї—О. пБљ –Ш—В–∞–Ї. –Ш–Љ–µ–µ–Љ —Д—Г–љ–Ї—Ж–Є—О –∞—А–≥—Г–Љ–µ–љ—В–∞: пБљ –Э–∞—Е–Њ–і–Є–Љ —З–∞—Б—В–љ—Л–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–µ –њ–µ—А–≤–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞:
- 16. пБљ –Ь–µ—В–Њ–і –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ –њ—А–Є–Љ–µ–љ–Є–Љ –Є –Ї —Г—А–∞–≤–љ–µ–љ–Є—О –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –≤ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Є—А–Њ–≤–∞–љ–љ–Њ–Љ –Љ–∞—Б—И—В–∞–±–µ: пБљ –≥–і–µ вАУ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Є—А–Њ–≤–∞–љ–љ—Л–µ –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ: , , –і–ї—П –Ї–Њ—В–Њ—А—Л—Е —Б—А–µ–і–љ–µ–µ –Ј–љ–∞—З–µ–љ–Є–µ —А–∞–≤–љ–Њ –љ—Г–ї—О: , –∞ —Б—А–µ–і–љ–µ–µ –Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ —А–∞–≤–љ–Њ –µ–і–Є–љ–Є—Ж–µ: ; вАУ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —А–µ–≥—А–µ—Б—Б–Є–Є.
- 17. пБљ –°—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —А–µ–≥—А–µ—Б—Б–Є–Є –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В, –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ –µ–і–Є–љ–Є—Ж –Є–Ј–Љ–µ–љ–Є—В—Б—П –≤ —Б—А–µ–і–љ–µ–Љ —А–µ–Ј—Г–ї—М—В–∞—В, –µ—Б–ї–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–є —Д–∞–Ї—В–Њ—А –Є–Ј–Љ–µ–љ–Є—В—Б—П –љ–∞ –Њ–і–љ—Г –µ–і–Є–љ–Є—Ж—Г –њ—А–Є –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–Љ —Б—А–µ–і–љ–µ–Љ —Г—А–Њ–≤–љ–µ –і—А—Г–≥–Є—Е —Д–∞–Ї—В–Њ—А–Њ–≤. –Т —Б–Є–ї—Г —В–Њ–≥–Њ, —З—В–Њ –≤—Б–µ –њ–µ—А–µ–Љ–µ–љ–љ—Л–µ –Ј–∞–і–∞–љ—Л –Ї–∞–Ї —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Є –љ–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ—Л–µ, —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —А–µ–≥—А–µ—Б—Б–Є–Є –Љ–Њ–ґ–љ–Њ —Б—А–∞–≤–љ–Є–≤–∞—В—М –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є. –°—А–∞–≤–љ–Є–≤–∞—П –Є—Е –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ, –Љ–Њ–ґ–љ–Њ —А–∞–љ–ґ–Є—А–Њ–≤–∞—В—М —Д–∞–Ї—В–Њ—А—Л –њ–Њ —Б–Є–ї–µ –Є—Е –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П –љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В. –Т —Н—В–Њ–Љ –Њ—Б–љ–Њ–≤–љ–Њ–µ –і–Њ—Б—В–Њ–Є–љ—Б—В–≤–Њ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —А–µ–≥—А–µ—Б—Б–Є–Є –≤ –Њ—В–ї–Є—З–Є–µ –Њ—В –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ ¬Ђ—З–Є—Б—В–Њ–є¬ї —А–µ–≥—А–µ—Б—Б–Є–Є, –Ї–Њ—В–Њ—А—Л–µ –љ–µ—Б—А–∞–≤–љ–Є–Љ—Л –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є.
- 18. пБљ –Я—А–Є–Љ–µ–љ—П—П –Ь–Э–Ъ –Ї —Г—А–∞–≤–љ–µ–љ–Є—О –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –≤ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Є—А–Њ–≤–∞–љ–љ–Њ–Љ –Љ–∞—Б—И—В–∞–±–µ, –њ–Њ–ї—Г—З–Є–Љ —Б–Є—Б—В–µ–Љ—Г –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є –≤–Є–і–∞ (2.5) пБљ –≥–і–µ –Є вАУ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –њ–∞—А–љ–Њ–є –Є –Љ–µ–ґ—Д–∞–Ї—В–Њ—А–љ–Њ–є –Ї–Њ—А—А–µ–ї—П—Ж–Є–Є. пБљ –Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л ¬Ђ—З–Є—Б—В–Њ–є¬ї —А–µ–≥—А–µ—Б—Б–Є–Є —Б–≤—П–Ј–∞–љ—Л —Б–Њ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є —А–µ–≥—А–µ—Б—Б–Є–Є —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
- 19. пБљ –†–∞—Б—Б–Љ–Њ—В—А–µ–љ–љ—Л–є —Б–Љ—Л—Б–ї —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —А–µ–≥—А–µ—Б—Б–Є–Є –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Є—Е –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –њ—А–Є –Њ—В—Б–µ–≤–µ —Д–∞–Ї—В–Њ—А–Њ–≤ вАУ –Є–Ј –Љ–Њ–і–µ–ї–Є –Є—Б–Ї–ї—О—З–∞—О—В—Б—П —Д–∞–Ї—В–Њ—А—Л —Б –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ –Ј–љ–∞—З–µ–љ–Є–µ–Љ . пБљ –Э–∞ –Њ—Б–љ–Њ–≤–µ –ї–Є–љ–µ–є–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є пБљ (2.7) пБљ –Љ–Њ–≥—Г—В –±—Л—В—М –љ–∞–є–і–µ–љ—Л —З–∞—Б—В–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є: (2.8) пБљ —В.–µ. —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є, –Ї–Њ—В–Њ—А—Л–µ —Б–≤—П–Ј—Л–≤–∞—О—В —А–µ–Ј—Г–ї—М—В–∞—В–Є–≤–љ—Л–є –њ—А–Є–Ј–љ–∞–Ї —Б —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–Љ —Д–∞–Ї—В–Њ—А–Њ–Љ –њ—А–Є –Ј–∞–Ї—А–µ–њ–ї–µ–љ–Є–Є –Њ—Б—В–∞–ї—М–љ—Л—Е —Д–∞–Ї—В–Њ—А–Њ–≤ –љ–∞ —Б—А–µ–і–љ–µ–Љ —Г—А–Њ–≤–љ–µ. –Т —А–∞–Ј–≤–µ—А–љ—Г—В–Њ–Љ –≤–Є–і–µ —Б–Є—Б—В–µ–Љ—Г (2.8) –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ–њ–Є—Б–∞—В—М –≤ –≤–Є–і–µ:
- 20. пБљ –Т –Њ—В–ї–Є—З–Є–µ –Њ—В –њ–∞—А–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є —З–∞—Б—В–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—В –Є–Ј–Њ–ї–Є—А–Њ–≤–∞–љ–љ–Њ–µ –≤–ї–Є—П–љ–Є–µ —Д–∞–Ї—В–Њ—А–∞ –љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В, –Є–±–Њ –і—А—Г–≥–Є–µ —Д–∞–Ї—В–Њ—А—Л –Ј–∞–Ї—А–µ–њ–ї–µ–љ—Л –љ–∞ –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–Љ —Г—А–Њ–≤–љ–µ. –≠—Д—Д–µ–Ї—В—Л –≤–ї–Є—П–љ–Є—П –і—А—Г–≥–Є—Е —Д–∞–Ї—В–Њ—А–Њ–≤ –њ—А–Є—Б–Њ–µ–і–Є–љ–µ–љ—Л –≤ –љ–Є—Е –Ї —Б–≤–Њ–±–Њ–і–љ–Њ–Љ—Г —З–ї–µ–љ—Г —Г—А–∞–≤–љ–µ–љ–Є—П –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є. –≠—В–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –љ–∞ –Њ—Б–љ–Њ–≤–µ —З–∞—Б—В–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є —А–µ–≥—А–µ—Б—Б–Є–Є –Њ–њ—А–µ–і–µ–ї—П—В—М —З–∞—Б—В–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В–Є:
- 21. пБљ –≥–і–µ вАУ–Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —А–µ–≥—А–µ—Б—Б–Є–Є –і–ї—П —Д–∞–Ї—В–Њ—А–∞ –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є, вАУ —З–∞—Б—В–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —А–µ–≥—А–µ—Б—Б–Є–Є. пБљ –Э–∞—А—П–і—Г —Б —З–∞—Б—В–љ—Л–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В–Є –Љ–Њ–≥—Г—В –±—Л—В—М –љ–∞–є–і–µ–љ—Л —Б—А–µ–і–љ–Є–µ –њ–Њ —Б–Њ–≤–Њ–Ї—Г–њ–љ–Њ—Б—В–Є –њ–Њ–Ї–∞–Ј–∞—В–µ–ї–Є —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В–Є: (2.11) пБљ –Ї–Њ—В–Њ—А—Л–µ –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ –њ—А–Њ—Ж–µ–љ—В–Њ–≤ –≤ —Б—А–µ–і–љ–µ–Љ –Є–Ј–Љ–µ–љ–Є—В—Б—П —А–µ–Ј—Г–ї—М—В–∞—В, –њ—А–Є –Є–Ј–Љ–µ–љ–µ–љ–Є–Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–≥–Њ —Д–∞–Ї—В–Њ—А–∞ –љ–∞ 1%. –°—А–µ–і–љ–Є–µ –њ–Њ–Ї–∞–Ј–∞—В–µ–ї–Є —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В–Є –Љ–Њ–ґ–љ–Њ —Б—А–∞–≤–љ–Є–≤–∞—В—М –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–љ–ґ–Є—А–Њ–≤–∞—В—М —Д–∞–Ї—В–Њ—А—Л –њ–Њ —Б–Є–ї–µ –Є—Е –≤–Њ–Ј–і–µ–є—Б—В–≤–Є—П –љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В.
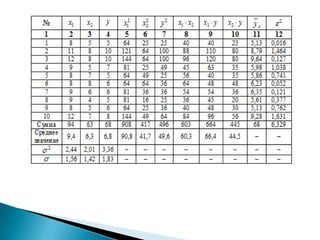
- 22. пБљ –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –њ—А–Є–Љ–µ—А (–і–ї—П —Б–Њ–Ї—А–∞—Й–µ–љ–Є—П –Њ–±—К–µ–Љ–∞ –≤—Л—З–Є—Б–ї–µ–љ–Є–є –Њ–≥—А–∞–љ–Є—З–Є–Љ—Б—П —В–Њ–ї—М–Ї–Њ –і–µ—Б—П—В—М—О –љ–∞–±–ї—О–і–µ–љ–Є—П–Љ–Є). –Я—Г—Б—В—М –Є–Љ–µ—О—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–µ –і–∞–љ–љ—Л–µ (—Г—Б–ї–Њ–≤–љ—Л–µ) –Њ —Б–Љ–µ–љ–љ–Њ–є –і–Њ–±—Л—З–µ —Г–≥–ї—П –љ–∞ –Њ–і–љ–Њ–≥–Њ —А–∞–±–Њ—З–µ–≥–Њ y (—В), –Љ–Њ—Й–љ–Њ—Б—В–Є –њ–ї–∞—Б—В–∞ (–Љ) –Є —Г—А–Њ–≤–љ–µ –Љ–µ—Е–∞–љ–Є–Ј–∞—Ж–Є–Є —А–∞–±–Њ—В (%), —Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є–µ –њ—А–Њ—Ж–µ—Б—Б –і–Њ–±—Л—З–Є —Г–≥–ї—П –≤ 10 —И–∞—Е—В–∞—Е. пБљ –Я—А–µ–і–њ–Њ–ї–∞–≥–∞—П, —З—В–Њ –Љ–µ–ґ–і—Г –њ–µ—А–µ–Љ–µ–љ–љ—Л–Љ–Є y , , —Б—Г—Й–µ—Б—В–≤—Г–µ—В –ї–Є–љ–µ–є–љ–∞—П –Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–∞—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М, –љ–∞–є–і–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ —А–µ–≥—А–µ—Б—Б–Є–Є y –њ–Њ –Є . пБљ –Ф–ї—П —Г–і–Њ–±—Б—В–≤–∞ –і–∞–ї—М–љ–µ–є—И–Є—Е –≤—Л—З–Є—Б–ї–µ–љ–Є–є —Б–Њ—Б—В–∞–≤–ї—П–µ–Љ —В–∞–±–ї–Є—Ж—Г ( ):
- 24. пБљ –Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ —Г—А–∞–≤–љ–µ–љ–Є—П —А–µ–≥—А–µ—Б—Б–Є–Є –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —А–µ—И–Є—В—М —Б–ї–µ–і—Г—О—Й—Г—О —Б–Є—Б—В–µ–Љ—Г –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є: пБљ –Ю—В–Ї—Г–і–∞ –њ–Њ–ї—Г—З–∞–µ–Љ, —З—В–Њ . –Ґ.–µ. –њ–Њ–ї—Г—З–Є–ї–Є —Б–ї–µ–і—Г—О—Й–µ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є: пБљ –Ю–љ–Њ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є —В–Њ–ї—М–Ї–Њ –Љ–Њ—Й–љ–Њ—Б—В–Є –њ–ї–∞—Б—В–∞ (–њ—А–Є –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–Љ ) –љ–∞ 1 –Љ –і–Њ–±—Л—З–∞ —Г–≥–ї—П –љ–∞ –Њ–і–љ–Њ–≥–Њ —А–∞–±–Њ—З–µ–≥–Њ y —Г–≤–µ–ї–Є—З–Є—В—Б—П –≤ —Б—А–µ–і–љ–µ–Љ –љ–∞ 0,854 —В, –∞ –њ—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є —В–Њ–ї—М–Ї–Њ —Г—А–Њ–≤–љ—П –Љ–µ—Е–∞–љ–Є–Ј–∞—Ж–Є–Є —А–∞–±–Њ—В (–њ—А–Є –љ–µ–Є–Ј–Љ–µ–љ–љ–Њ–Љ ) –љ–∞ 1% вАУ –≤ —Б—А–µ–і–љ–µ–Љ –љ–∞ 0,367 —В.
- 25. пБљ –Э–∞–є–і–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–є —А–µ–≥—А–µ—Б—Б–Є–Є –≤ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ–Њ–Љ –Љ–∞—Б—И—В–∞–±–µ: пБљ –њ—А–Є —Н—В–Њ–Љ —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —А–µ–≥—А–µ—Б—Б–Є–Є –±—Г–і—Г—В пБљ –Ґ.–µ. —Г—А–∞–≤–љ–µ–љ–Є–µ –±—Г–і–µ—В –≤—Л–≥–ї—П–і–µ—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: пБљ –Ґ–∞–Ї –Ї–∞–Ї —Б—В–∞–љ–і–∞—А—В–Є–Ј–Њ–≤–∞–љ–љ—Л–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —А–µ–≥—А–µ—Б—Б–Є–Є –Љ–Њ–ґ–љ–Њ —Б—А–∞–≤–љ–Є–≤–∞—В—М –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є, —В–Њ –Љ–Њ–ґ–љ–Њ —Б–Ї–∞–Ј–∞—В—М, —З—В–Њ –Љ–Њ—Й–љ–Њ—Б—В—М –њ–ї–∞—Б—В–∞ –Њ–Ї–∞–Ј—Л–≤–∞–µ—В –±–Њ–ї—М—И–µ–µ –≤–ї–Є—П–љ–Є–µ –љ–∞ —Б–Љ–µ–љ–љ—Г—О –і–Њ–±—Л—З—Г —Г–≥–ї—П, —З–µ–Љ —Г—А–Њ–≤–µ–љ—М –Љ–µ—Е–∞–љ–Є–Ј–∞—Ж–Є–Є —А–∞–±–Њ—В.
- 26. пБљ –°—А–∞–≤–љ–Є–≤–∞—В—М –≤–ї–Є—П–љ–Є–µ —Д–∞–Ї—В–Њ—А–Њ–≤ –љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В –Љ–Њ–ґ–љ–Њ —В–∞–Ї–ґ–µ –њ—А–Є –њ–Њ–Љ–Њ—Й–Є —Б—А–µ–і–љ–Є—Е –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —Н–ї–∞—Б—В–Є—З–љ–Њ—Б—В–Є (2.11): пБљ –Т—Л—З–Є—Б–ї—П–µ–Љ: пБљ –Ґ.–µ. —Г–≤–µ–ї–Є—З–µ–љ–Є–µ —В–Њ–ї—М–Ї–Њ –Љ–Њ—Й–љ–Њ—Б—В–Є –њ–ї–∞—Б—В–∞ (–Њ—В —Б–≤–Њ–µ–≥–Њ —Б—А–µ–і–љ–µ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П) –Є–ї–Є —В–Њ–ї—М–Ї–Њ —Г—А–Њ–≤–љ—П –Љ–µ—Е–∞–љ–Є–Ј–∞—Ж–Є–Є —А–∞–±–Њ—В –љ–∞ 1% —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В –≤ —Б—А–µ–і–љ–µ–Љ —Б–Љ–µ–љ–љ—Г—О –і–Њ–±—Л—З—Г —Г–≥–ї—П –љ–∞ 1,18% –Є–ї–Є 0,34% —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ–Њ–і—В–≤–µ—А–ґ–і–∞–µ—В—Б—П –±–Њ–ї—М—И–µ–µ –≤–ї–Є—П–љ–Є–µ –љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В y —Д–∞–Ї—В–Њ—А–∞ , —З–µ–Љ —Д–∞–Ї—В–Њ—А–∞ .