マハラノビス距离とユークリッド距离の违い
- 1. 2011.02 作成 マハラノビス距离とユークリッド距离の违い 車のスピードと停車するまでに必要な距 離を測定した2変数の cars データセットを 100 120 用いて、データ中心からの各データポイント 図1 の距離を測定する。 我々が通常距離と呼んでいるものはユーク 80 リッド距離だが、相関のある多変量データを dist 60 取り扱う際にはマハラノビス距離の方が便利。 40 方法 1 標準化してユークリッド距離を測定 20 変数 dist と speed はそれぞれ尺度が違う 0 のでそのままで距離計算をすると第 1 変数 5 10 15 20 25 の影響が第 2 変数よりも大きくなる。 speed これを避けるために、 まず2変数をそれぞ れ標準化し(図 2)、それから二乗和の平方根 をとって距離を計算する。 3 Histogram of d1 図2 2 図3 1 15 dist Frequency 10 0 -1 5 0 -2 -1 0 1 speed 0 40 80 120 3 d1 図4 2 距離 d1 が 120 を越える外れ値は 49 番のデ 1 dist ータポイント。次に他のデータから外れ気 0 味なのは緑で示すデータポイントで、距離 が遠い順に 48, 47, 509, 35, 23 番が分布の -1 外側にあるということになる。 -2 -1 0 1 speed
- 2. 方法 2 マハラノビス距離による測定 方法 1 のユークリッド距離のかわりに、平均値ベクトルと共分散行列から算出するマハ ラノビス距離を使用してみる。 方法 1 と同様、ヒストグラム(図 5)を作成し、で大きな距離とる柱二つ分の色を変えて データポイントを表示したのが図 6。緑表示されているのは、データ番号 23 番のみ。 Histogram of d2 120 図5 30 80 Frequency dist 20 40 10 0 0 0 2 4 6 8 10 5 10 15 20 25 d2 speed 「標準化+ユークリッド距離」と「マハラノビス距離」の違いは、マ ハラノビス距離がデータ分散だけでなく相関も考慮しているというこ と。つまり、データを多変量標準化して距離尺度を作成していること になる。 ○ マハラノビス距離 平均値ベクトルが 、共分散行列がΣである多変量デー タ は、以下により算出される。
- 3. おまけ:マハラノビス距离とユークリッド距离の违い データ NmA は、独立なデータ数 1000 の正規乱数を二つ組み合わせたもので、NmB もデ ータ数 1000 の正規乱数だが変数間に 0.8 の相関がある。 この二種類のデータについて、それぞれユークリッド距離とマハラノビス距離を計算し、 データ中心から距離 2 以内の部分を緑、さらに距離 1 以内の部分を赤に塗ってみた。 無相関ユーク ッ リド 無相関マ ノ ス ハラ ビ 3 3 2 2 1 1 NmA[,2] NmA[,2] 0 0 -1 -1 -2 -2 -3 -3 -3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3 NmA[,1] NmA[,1] 相関0.8ユーク ッ リド 相関0.8マ ノ ス ハラ ビ 3 3 2 2 NmB[,2] NmB[,2] 1 1 0 0 -1 -1 -2 -2 -3 -3 -3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3 NmB[,1] NmB[,1] データが正規分布に従う場合、各データポイントのデータ中心(平均値ベクトル)から のマハラノビス距離は F 分布に従う。
- 4. Rコード data(cars) # cars データ呼び出し dat<- as.matrix(cars) # リスト属性の cars データを行列属性に変換して dat に格納 d <- ncol(dat) # d: 変数の数 n <- nrow(dat) # n: データ数 plot(dat) # 図 1 が表示される ##### ユークリッド距離による試算 dat.s<- scale(dat) # 標準化 plot(dat.s) # 図 2 が表示される d1 <- sqrt(dat[,1]^2 + dat[,2]^2) # 第一変数と第二変数の二乗和の平方根で距 離計算 hist(d1) # 計算された距離をヒストグラムに。図 3。 flg<- rep(1, n) # 色表示用のデータフラグ作成。初期値は 1(黒) flg[which(d1>80)] <- 3 # 距離 d1 が 80 を越えるデータを 3(緑)に flg[which(d1>120)] <- 2 # 距離 d1 が 120 を越えるデータを 2(赤)に plot(dat.s, pch=20, col=flg) # 図 4 表示 which(flg==2) # 赤表示されるデータの番号がわかる。No.49 which(flg==3) # 緑表示されるデータの番号がわかる。No. 23, 35, 47, 48, 509 ##### マハラノビス距離による試算 cv <- cov(dat) # 共分散行列計算 mn<- colMeans(dat) # 平均値ベクトル算出 d2 <- mahalanobis(dat, mn, cv) # マハラノビス距離算出 hist(d2) # 図 5 の表示 flg2 <- rep(1, n) # 色表示用のデータフラグ作成。初期値は 1(黒) flg2[which(d2>6)] <- 3 # 距離 d1 が 6 を越えるデータだけ 3(緑)に flg2[which(d2>8)] <- 2 # 距離 d1 が 8 を越えるデータだけ 2(赤)に plot(dat, pch=20, col=flg2) # 図 4 表示 which(flg2==2) # 赤表示されるデータの番号がわかる。No.49
- 5. #################### おまけ #################### rm(list=ls(all=TRUE)) # 作業領域のクリア library(mvtnorm) # rmvnorm(多変量正規乱数)関数用 set.seed(25) # 乱数の再現性確保のため # 共分散行列作成 c08 <- matrix(0.8, ncol=2, nrow=2) # # 対角成分を 1 に (diag(c08) <- 1) # 算式を括弧で囲むと内容表示 n1 <- 1000 # 作成するデータ数 # 正規分布データ NmA<- cbind(rnorm(n1), rnorm(n1)) # 単変量の独立な正規分布データを組み合わせただけ NmB<- rmvnorm(n=n1, mean=c(0, 0), sigma=c08) # 相関 0.8 の多変量正規分布データ cor(NmA); cor(NmB) # 実相関 # ユークリッド距離の計算 #eucA<- sqrt(diag(scale(NmA) %*% t(scale(NmA)))) #eucB<- sqrt(diag(scale(NmB) %*% t(scale(NmB)))) eucA<- sqrt(diag(NmA %*% t(NmA))) eucB<- sqrt(diag(NmB %*% t(NmB))) #マハラノビス距離の計算 mahA<- mahalanobis(NmA, apply(NmA, 2, mean), cov(NmA)) mahB<- mahalanobis(NmB, apply(NmB, 2, mean), cov(NmB)) # パラメータはデータ?平均値ベクトル?共分散行列 # ユークリッド距離と比較可能にする # F 検定統計量の計算 eucA.s <- eucA * (n1 - 2)* n1 /((n1^2 - 1)* 2) eucB.s<- eucB * (n1 - 2)* n1 /((n1^2 - 1)* 2) mahA.s <- mahA * (n1 - 2)* n1 /((n1^2 - 1)* 2) mahB.s<- mahB * (n1 - 2)* n1 /((n1^2 - 1)* 2) # 正規分布の 1σ(約 68.27%) 、2σ(約 95.45%)にあたるF分布の%値を算出 cf1<- qf(0.6827,2, n1 - 2) cf2<- qf(0.9545, 2, n1 - 2) # 色設定 距離 1 より内側を赤に eucA.cl <- rep(1, 1000); eucA.cl[which(eucA< 2)] <- 3 eucA.cl[which(eucA< 1)] <- 2 eucB.cl <- rep(1, 1000); eucB.cl[which(eucB< 2)] <- 3
- 6. eucB.cl[which(eucB< 1)] <- 2 mahA.cl <- rep(1, 1000); mahA.cl[which(mahA.s<cf2)] <- 3 mahA.cl[which(mahA.s<cf1)] <- 2 mahB.cl <- rep(1, 1000); mahB.cl[which(mahB.s<cf2)] <- 3 mahB.cl[which(mahB.s<cf1)] <- 2 par(mfrow=c(2,2)) # 2 行 2 列にグラフィック画面分割 plot(NmA, pch=20, col=eucA.cl, main="無相関ユークリッド") plot(NmA, pch=20, col=mahA.cl, main="無相関マハラノビス") plot(NmB, pch=20, col=eucB.cl, main="相関 0.8 ユークリッド") plot(NmB, pch=20, col=mahB.cl, main="相関 0.8 マハラノビス")

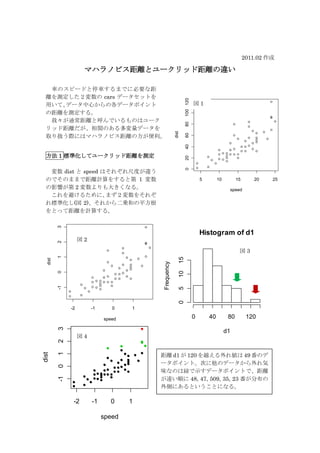

![おまけ:マハラノビス距离とユークリッド距离の违い
データ NmA は、独立なデータ数 1000 の正規乱数を二つ組み合わせたもので、NmB もデ
ータ数 1000 の正規乱数だが変数間に 0.8 の相関がある。
この二種類のデータについて、それぞれユークリッド距離とマハラノビス距離を計算し、
データ中心から距離 2 以内の部分を緑、さらに距離 1 以内の部分を赤に塗ってみた。
無相関ユーク ッ
リド 無相関マ ノ ス
ハラ ビ
3
3
2
2
1
1
NmA[,2]
NmA[,2]
0
0
-1
-1
-2
-2
-3
-3
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
NmA[,1] NmA[,1]
相関0.8ユーク ッ
リド 相関0.8マ ノ ス
ハラ ビ
3
3
2
2
NmB[,2]
NmB[,2]
1
1
0
0
-1
-1
-2
-2
-3
-3
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
NmB[,1] NmB[,1]
データが正規分布に従う場合、各データポイントのデータ中心(平均値ベクトル)から
のマハラノビス距離は F 分布に従う。](https://image.slidesharecdn.com/slideshare-121217051446-phpapp02/85/-3-320.jpg)
![Rコード
data(cars) # cars データ呼び出し
dat<- as.matrix(cars) # リスト属性の cars データを行列属性に変換して
dat に格納
d <- ncol(dat) # d: 変数の数
n <- nrow(dat) # n: データ数
plot(dat) # 図 1 が表示される
##### ユークリッド距離による試算
dat.s<- scale(dat) # 標準化
plot(dat.s) # 図 2 が表示される
d1 <- sqrt(dat[,1]^2 + dat[,2]^2) # 第一変数と第二変数の二乗和の平方根で距
離計算
hist(d1) # 計算された距離をヒストグラムに。図 3。
flg<- rep(1, n) # 色表示用のデータフラグ作成。初期値は 1(黒)
flg[which(d1>80)] <- 3 # 距離 d1 が 80 を越えるデータを 3(緑)に
flg[which(d1>120)] <- 2 # 距離 d1 が 120 を越えるデータを 2(赤)に
plot(dat.s, pch=20, col=flg) # 図 4 表示
which(flg==2) # 赤表示されるデータの番号がわかる。No.49
which(flg==3) # 緑表示されるデータの番号がわかる。No. 23, 35, 47, 48,
509
##### マハラノビス距離による試算
cv <- cov(dat) # 共分散行列計算
mn<- colMeans(dat) # 平均値ベクトル算出
d2 <- mahalanobis(dat, mn, cv) # マハラノビス距離算出
hist(d2) # 図 5 の表示
flg2 <- rep(1, n) # 色表示用のデータフラグ作成。初期値は 1(黒)
flg2[which(d2>6)] <- 3 # 距離 d1 が 6 を越えるデータだけ 3(緑)に
flg2[which(d2>8)] <- 2 # 距離 d1 が 8 を越えるデータだけ 2(赤)に
plot(dat, pch=20, col=flg2) # 図 4 表示
which(flg2==2) # 赤表示されるデータの番号がわかる。No.49](https://image.slidesharecdn.com/slideshare-121217051446-phpapp02/85/-4-320.jpg)
![#################### おまけ ####################
rm(list=ls(all=TRUE)) # 作業領域のクリア
library(mvtnorm) # rmvnorm(多変量正規乱数)関数用
set.seed(25) # 乱数の再現性確保のため
# 共分散行列作成
c08 <- matrix(0.8, ncol=2, nrow=2)
# # 対角成分を 1 に
(diag(c08) <- 1) # 算式を括弧で囲むと内容表示
n1 <- 1000 # 作成するデータ数
# 正規分布データ
NmA<- cbind(rnorm(n1), rnorm(n1))
# 単変量の独立な正規分布データを組み合わせただけ
NmB<- rmvnorm(n=n1, mean=c(0, 0), sigma=c08)
# 相関 0.8 の多変量正規分布データ
cor(NmA); cor(NmB) # 実相関
# ユークリッド距離の計算
#eucA<- sqrt(diag(scale(NmA) %*% t(scale(NmA))))
#eucB<- sqrt(diag(scale(NmB) %*% t(scale(NmB))))
eucA<- sqrt(diag(NmA %*% t(NmA)))
eucB<- sqrt(diag(NmB %*% t(NmB)))
#マハラノビス距離の計算
mahA<- mahalanobis(NmA, apply(NmA, 2, mean), cov(NmA))
mahB<- mahalanobis(NmB, apply(NmB, 2, mean), cov(NmB))
# パラメータはデータ?平均値ベクトル?共分散行列
# ユークリッド距離と比較可能にする
# F 検定統計量の計算
eucA.s <- eucA * (n1 - 2)* n1 /((n1^2 - 1)* 2)
eucB.s<- eucB * (n1 - 2)* n1 /((n1^2 - 1)* 2)
mahA.s <- mahA * (n1 - 2)* n1 /((n1^2 - 1)* 2)
mahB.s<- mahB * (n1 - 2)* n1 /((n1^2 - 1)* 2)
# 正規分布の 1σ(約 68.27%) 、2σ(約 95.45%)にあたるF分布の%値を算出
cf1<- qf(0.6827,2, n1 - 2)
cf2<- qf(0.9545, 2, n1 - 2)
# 色設定 距離 1 より内側を赤に
eucA.cl <- rep(1, 1000);
eucA.cl[which(eucA< 2)] <- 3
eucA.cl[which(eucA< 1)] <- 2
eucB.cl <- rep(1, 1000);
eucB.cl[which(eucB< 2)] <- 3](https://image.slidesharecdn.com/slideshare-121217051446-phpapp02/85/-5-320.jpg)
![eucB.cl[which(eucB< 1)] <- 2
mahA.cl <- rep(1, 1000);
mahA.cl[which(mahA.s<cf2)] <- 3
mahA.cl[which(mahA.s<cf1)] <- 2
mahB.cl <- rep(1, 1000);
mahB.cl[which(mahB.s<cf2)] <- 3
mahB.cl[which(mahB.s<cf1)] <- 2
par(mfrow=c(2,2)) # 2 行 2 列にグラフィック画面分割
plot(NmA, pch=20, col=eucA.cl, main="無相関ユークリッド")
plot(NmA, pch=20, col=mahA.cl, main="無相関マハラノビス")
plot(NmB, pch=20, col=eucB.cl, main="相関 0.8 ユークリッド")
plot(NmB, pch=20, col=mahB.cl, main="相関 0.8 マハラノビス")](https://image.slidesharecdn.com/slideshare-121217051446-phpapp02/85/-6-320.jpg)