Žįėžā¨Ž≤°ŪĄį
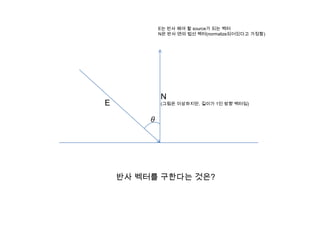
- 1. EŽäĒ Žįėžā¨ Ūēīžēľ Ūē† sourceÍįÄ ŽźėŽäĒ Ž≤°ŪĄį NžĚÄ Žįėžā¨ Ž©īžĚė Ž≤ēžĄ† Ž≤°ŪĄį(normalizeŽźėžĖīžěąŽč§Í≥† ÍįÄž†ēŪē®) N E (Í∑łŽ¶ľžĚÄ žĚīžÉĀŪēėžßÄŽßĆ, ÍłłžĚīÍįÄ 1žĚł Žį©ŪĖ• Ž≤°ŪĄįžěĄ) Žįėžā¨ Ž≤°ŪĄįŽ•ľ ÍĶ¨ŪēúŽč§ŽäĒ Í≤ÉžĚÄ?
- 2. N E žĚī ŽĻ®ÍįĄ žĄ†žĚė Ž≤°ŪĄįŽ•ľ ÍĶ¨ŪēėÍ≥† žč∂Žč§ŽäĒ Í≤É
- 3. N -E žēĄžĚīŽĒĒžĖīŽäĒ žēĄž£ľ ÍįĄŽč®ŪēėŽč§. 1. EŽ•ľ Ží§žßĎžĖīžĄú ( -E)
- 4. N -E 2. -EžôÄ NžĚĄ Žāīž†ĀŪēú Í≤Éžóź (Žāīž†ĀŪēėŽ©ī ŽĻ®ÍįĄ žĄ†žĚė ÍłłžĚīÍįÄ Žāėžė®Žč§.) ž≤®Ž∂ÄžĄ§Ž™Ö : Žāīž†ĀžĚī ŽĻ®ÍįĄ žĄ†žĚė ÍłłžĚīÍįÄ ŽźėŽäĒ žĚīžú† žßĀÍįĀ žāľÍįĀŪėēžĚīŽĚľÍ≥† žÉĚÍįĀŪēėŽ©ī, cos@ = ŽįĎŽ≥Ä/ŽĻóŽ≥Ä ( ||N|| / ||E||) ŽįĎŽ≥Ä = ŽĻóŽ≥Ä * cos@ ( ŽĻ®ÍįĄ žĄ†žĚė ÍłłžĚī = ||E|| cos@ )
- 5. N -E 3. Í∑ł ÍłłžĚīžĚė ŽĎź ŽįįŽ°ú ŽßƎ吏ĖīžĄú Žāīž†ĀžĚė ÍįížĚÄ scalar ž¶Č, Ūēú ÍįúžĚė ÍįížĚīŽč§.(float[1])
- 6. N -E 4. NŽį©ŪĖ•žĚĄ ÍįÄžßÄŽäĒ Ž≤°ŪĄįžóź Í≥ĪŪēīž£ľÍ≥† Žį©ŪĖ• Ž≤°ŪĄį(ÍłłžĚīÍįÄ 1žĚł)žóź ÍłłžĚī Íįí (len)žĚĄ Í≥ĪŪēėŽ©ī, ÍłłžĚīŽßĆ (len)Ž°ú ŽäėžĖīŽāú ÍįôžĚÄ Žį©ŪĖ•žĚĄ ÍįÄŽ¶¨Ūā§ŽäĒ Ž≤°ŪĄįÍįÄ Žāėžė®Žč§.
- 7. E N E 4. ÍĪįÍłįžóź EŽ•ľ ŽćĒŪēėŽ©ī ÍĶ¨ŪēėÍ≥†žěź ŪĖąŽćė Žįėžā¨Ž≤°ŪĄįŽ•ľ ÍĶ¨Ūē† žąėÍįÄ žěąŽč§. ŽĎź Ž≤°ŪĄįŽ•ľ ŽćĒŪēėŽ©ī, žõźž†źžóźžĄú ŽĎź Ž≤°ŪĄįŽßĆŪĀľ žĚīŽŹôŪēú žúĄžĻėŽ°ú ŪĖ•ŪēėŽäĒ Ž≤°ŪĄįÍįÄ ŽßƎ吏ĖīžßĄŽč§. ž¶Č, ŽĻ®ÍįĄ Ž≤°ŪĄį ŽĎź ÍįúŽ•ľ ŽćĒŪēėŽ©ī ŽÖĻžÉČ Ž≤°ŪĄįÍįÄ Žāėžėī.
- 8. E N E



![N
-E
3. Í∑ł ÍłłžĚīžĚė ŽĎź ŽįįŽ°ú ŽßƎ吏ĖīžĄú
Žāīž†ĀžĚė ÍįížĚÄ scalar
ž¶Č, Ūēú ÍįúžĚė ÍįížĚīŽč§.(float[1])](https://image.slidesharecdn.com/random-130317214532-phpapp02/85/-5-320.jpg)


