–ü–ĺ–Ĺ—Ź—ā—ā—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó
- 1. –Ę–Ķ–ľ–į: –§—É–Ĺ–ļ—Ü—Ė—Ź. 1. –ü–ĺ–Ĺ—Ź—ā—ā—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó. 2. –°–Ņ–ĺ—Ā–ĺ–Ī–ł –∑–į–ī–į–Ĺ–Ĺ—Ź —Ą—É–Ĺ–ļ—Ü—Ė–Ļ. 3. –ö–Ľ–į—Ā–ł—Ą—Ė–ļ–į—Ü—Ė—Ź –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ł—Ö —Ą—É–Ĺ–ļ—Ü—Ė–Ļ. 4. –ú–ĺ–Ĺ–ĺ—ā–ĺ–Ĺ–Ĺ—Ė —Ą—É–Ĺ–ļ—Ü—Ė—ó. 5. –ü–į—Ä–Ĺ—Ė —ā–į –Ĺ–Ķ–Ņ–į—Ä–Ĺ—Ė —Ą—É–Ĺ–ļ—Ü—Ė—ó. 6. –ü–Ķ—Ä—Ė–ĺ–ī–ł—á–Ĺ—Ė —Ą—É–Ĺ–ļ—Ü—Ė—ó. 7. –ü–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė–Ļ.
- 2. –ě–∑–Ĺ. 1. –§—É–Ĺ–ļ—Ü—Ė—Ē—é –Ĺ–į–∑–ł–≤–į—é—ā—Ć –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ—Ė—Ā—ā—Ć –ľ—Ė–∂ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł –ī–≤–ĺ—Ö –ľ–Ĺ–ĺ–∂–ł–Ĺ —Ö —ā–į —É, –Ņ—Ä–ł —Ź–ļ—Ė–Ļ –ļ–ĺ–∂–Ĺ–ĺ–ľ—É –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤—Ė –Ņ–Ķ—Ä—ą–ĺ—ó –ľ–Ĺ–ĺ–∂–ł–Ĺ–ł —Ö –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–į—Ē –Ĺ–Ķ –Ī—Ė–Ľ—Ć—ą–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į —É –ī—Ä—É–≥–ĺ—ó –ľ–Ĺ–ĺ–∂–ł–Ĺ–ł. –• –£
- 3. –ó–ľ—Ė–Ĺ–Ĺ–į —Ö –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ĺ–Ķ–∑–į–Ľ–Ķ–∂–Ĺ–ĺ—é –∑–ľ—Ė–Ĺ–Ĺ–ĺ—é, –į–Ī–ĺ –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–ľ, –į –∑–ľ—Ė–Ĺ–Ĺ–į —É ‚Äď –∑–į–Ľ–Ķ–∂–Ĺ–ĺ—é –∑–ľ—Ė–Ĺ–Ĺ–ĺ—é, –į–Ī–ĺ —Ą—É–Ĺ–ļ—Ü—Ė—Ē—é. –ü—Ė–ī —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ —É = f(—Ö) —Ä–ĺ–∑—É–ľ—Ė—é—ā—Ć —ā–Ķ –Ņ—Ä–į–≤–ł–Ľ–ĺ, –∑–į —Ź–ļ–ł–ľ –ļ–ĺ–∂–Ĺ–ĺ–ľ—É —Ö –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–į—Ē —É, –į–Ī–ĺ —ā—Ė –ĺ–Ņ–Ķ—Ä–į—Ü—Ė—ó, —Ź–ļ—Ė —ā—Ä–Ķ–Ī–į –≤–ł–ļ–ĺ–Ĺ–į—ā–ł –Ĺ–į–ī –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–ľ, —Č–ĺ–Ī –ī—Ė—Ā—ā–į—ā–ł –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó.
- 4. –ě–∑–Ĺ. 2: –ú–Ĺ–ĺ–∂–ł–Ĺ–į –≤—Ā—Ė—Ö —ā–ł—Ö –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā—Ė–≤ –∑ –•, –ī–Ľ—Ź —Ź–ļ–ł—Ö —Ē –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ—Ė –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł –ľ–Ĺ–ĺ–∂–ł–Ĺ–ł –£, –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –ĺ–Ī–Ľ–į—Ā—ā—é –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź, –į –ľ–Ĺ–ĺ–∂–ł–Ĺ–į –≤—Ā—Ė—Ö —ā–ł—Ö –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā—Ė–≤ –∑ –£, —Č–ĺ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–į—é—ā—Ć –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ –∑ –•, ‚ąí –ĺ–Ī–Ľ–į—Ā—ā—é –∑–Ĺ–į—á–Ķ–Ĺ—Ć –ī–į–Ĺ–ĺ—ó —Ą—É–Ĺ–ļ—Ü—Ė—ó. –ü—Ä–ł–ļ–Ľ–į–ī: –Ē–Ľ—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó —É = —Ö + 4 –ĺ–Ī–Ľ–į—Ā—ā—Ć –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź: —Ö —Ē R. –ě–Ī–Ľ–į—Ā—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ—Ć: —É —Ē R . –Ē–Ľ—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó –ĺ–Ī–Ľ–į—Ā—ā—Ć –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź: –ĺ–Ī–Ľ–į—Ā—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ—Ć: √Ķ √≥ 4 ÔÄĹ ÔÄ® ÔÄ© ÔÄ® ÔÄ© ÔÄęÔā• ÔÉą Ôā• ÔÄ≠ ÔÉé ; 0 0 ; —Ö ÔÄ® ÔÄ© ÔÄ® ÔÄ© ÔÄęÔā• ÔÉą Ôā• ÔÄ≠ ÔÉé ; 0 0 ; —É
- 5. –ě–∑–Ĺ. 3: –ď—Ä–į—Ą—Ė–ļ–ĺ–ľ —Ą—É–Ĺ–ļ—Ü—Ė—ó f –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –ľ–Ĺ–ĺ–∂–ł–Ĺ–į —ā–ĺ—á–ĺ–ļ (—Ö;—É) –Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ—Ė–Ļ –Ņ–Ľ–ĺ—Č–ł–Ĺ—Ė, —ā–į–ļ–ł—Ö, —Č–ĺ –Ņ–Ķ—Ä–Ķ–Ī—Ė–≥–į—é—ā—Ć –≤—Ā—é –ľ–Ĺ–ĺ–∂–ł–Ĺ—É D(f), –į —É = f(—Ö). —É=2—Ö+3.
- 6. –°–Ņ–ĺ—Ā–ĺ–Ī–ł –∑–į–ī–į–Ĺ–Ĺ—Ź —Ą—É–Ĺ–ļ—Ü—Ė—ó –ź–Ĺ–į–Ľ—Ė—ā–ł—á–Ĺ–ł–Ļ –ď—Ä–į—Ą—Ė—á–Ĺ–ł–Ļ –Ę–į–Ī–Ľ–ł—á–Ĺ–ł–Ļ —É=2—Ö-3 —Ö 0 1 —É -3 -1
- 7. –ě–∑–Ĺ. 4: –õ—Ė–Ĺ—Ė–Ļ–Ĺ–ĺ—é –Ĺ–į–∑–ł–≤–į—é—ā—Ć —Ą—É–Ĺ–ļ—Ü—Ė—é, —Ź–ļ—É –ľ–ĺ–∂–Ĺ–į –∑–į–ī–į—ā–ł —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é —É = –į—Ö + b, –ī–Ķ —Ö ‚Äď –į—Ä–≥—É–ľ–Ķ–Ĺ—ā, –į —Ė b ‚Äď –Ī—É–ī—Ć-—Ź–ļ—Ė —á–ł—Ā–Ľ–į. 1.–ě–Ī–Ľ–į—Ā—ā—Ć –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź: —Ö —Ē R . 2.–ě–Ī–Ľ–į—Ā—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ—Ć: —É —Ē R . 3.–ü—Ä–ł –į>0 —Ą—É–Ĺ–ļ—Ü—Ė—Ź –∑—Ä–ĺ—Ā—ā–į—Ē, –Ņ—Ä–ł –į<0 —Ā–Ņ–į–ī–į—Ē.
- 8. –ě–∑–Ĺ. 5: –ó–ľ—Ė–Ĺ–Ĺ—É —É –Ĺ–į–∑–ł–≤–į—é—ā—Ć –ĺ–Ī–Ķ—Ä–Ĺ–Ķ–Ĺ–ĺ –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü—Ė–Ļ–Ĺ–ĺ—é –ī–ĺ –∑–ľ—Ė–Ĺ–Ĺ–ĺ—ó —Ö, —Ź–ļ—Č–ĺ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ—Ė –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —Ü–ł—Ö –∑–ľ—Ė–Ĺ–Ĺ–ł—Ö –∑–≤‚Äô—Ź–∑–į–Ĺ—Ė —Ä—Ė–≤–Ĺ—Ė—Ā—ā—é 1.–ě–Ī–Ľ–į—Ā—ā—Ć –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź: 2.–ě–Ī–Ľ–į—Ā—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ—Ć: 3.–ü—Ä–ł k>0 —Ą—É–Ĺ–ļ—Ü—Ė—Ź —Ā–Ņ–į–ī–į—Ē, –Ņ—Ä–ł k<0‚Äď–∑—Ä–ĺ—Ā—ā–į—Ē. ÔÄ® ÔÄ© ÔÄ® ÔÄ© ÔÄęÔā• ÔÉą Ôā• ÔÄ≠ ÔÉé ; 0 0 ; —Ö ÔÄ® ÔÄ© ÔÄ® ÔÄ© ÔÄęÔā• ÔÉą Ôā• ÔÄ≠ ÔÉé ; 0 0 ; —É —Ö k —É ÔÄĹ
- 9. –ě–∑–Ĺ. 6: –ö–≤–į–ī—Ä–į—ā–ł—á–Ĺ–ĺ—é –Ĺ–į–∑–ł–≤–į—é—ā—Ć —Ą—É–Ĺ–ļ—Ü—Ė—é, —Ź–ļ—É –ľ–ĺ–∂–Ĺ–į –∑–į–ī–į—ā–ł —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é —É=–į—Ö2+b—Ö+—Ā, –ī–Ķ —Ö ‚Äď –∑–ľ—Ė–Ĺ–Ĺ–į, –į ‚Ȇ 0, b —Ė —Ā ‚Äď —á–ł—Ā–Ľ–į. 1. –ě–Ī–Ľ–į—Ā—ā—Ć –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź: —Ö —Ē R . 2. –ě–Ī–Ľ–į—Ā—ā—Ć –∑–Ĺ–į—á–Ķ–Ĺ—Ć: —É —Ē R . –ď—Ä–į—Ą—Ė–ļ–ĺ–ľ –ļ–≤–į–ī—Ä–į—ā–ł—á–Ĺ–ĺ—ó —Ą—É–Ĺ–ļ—Ü—Ė—ó —Ē –Ņ–į—Ä–į–Ī–ĺ–Ľ–į; —Ź–ļ—Č–ĺ –į>0, —ā–ĺ —ó—ó –≥—Ė–Ľ–ļ–ł –Ĺ–į–Ņ—Ä—Ź–ľ–Ľ–Ķ–Ĺ—Ė –≤–≥–ĺ—Ä—É; —Ź–ļ—Č–ĺ –į < 0, —ā–ĺ —ó—ó –≥—Ė–Ľ–ļ–ł –Ĺ–į–Ņ—Ä—Ź–ľ–Ľ–Ķ–Ĺ—Ė –≤–Ĺ–ł–∑. –í–Ķ—Ä—ą–ł–Ĺ–į —Ü—Ė—Ē—ó –Ņ–į—Ä–į–Ī–ĺ–Ľ–ł –ľ–į—Ē –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł ÔÉ∑ ÔÉł ÔÉ∂ ÔÉß ÔÉ® Ôɶ ÔÄ≠ ÔÄ≠ a b c a b 4 ; 2 2
- 10. –į<0, D<0 –į<0, D>0 –į<0, D=0 –į>0, D<0 –į>0, D>0 –į>0, D=0
- 11. –ú–ĺ–Ĺ–ĺ—ā–ĺ–Ĺ–Ĺ—Ė —Ą—É–Ĺ–ļ—Ü—Ė—ó –ě–∑–Ĺ. 7: –Ě–Ķ—Ö–į–Ļ —Ą—É–Ĺ–ļ—Ü—Ė—Ź —É = f(—Ö) –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–į –Ĺ–į –ľ–Ĺ–ĺ–∂–ł–Ĺ—Ė –ź. –Į–ļ—Č–ĺ –ī–Ľ—Ź –ī–≤–ĺ—Ö –ī–ĺ–≤—Ė–Ľ—Ć–Ĺ–ł—Ö —Ä—Ė–∑–Ĺ–ł—Ö –∑–Ĺ–į—á–Ķ–Ĺ—Ć —Ö1 —Ė —Ö2 –į—Ä–≥—É–ľ–Ķ–Ĺ—ā—É, –≤–∑—Ź—ā–ł—Ö —Ė–∑ –ľ–Ĺ–ĺ–∂–ł–Ĺ–ł –ź, –∑ –Ĺ–Ķ—Ä—Ė–≤–Ĺ–ĺ—Ā—ā—Ė —Ö1 < —Ö2 –≤–ł–Ņ–Ľ–ł–≤–į—Ē, —Č–ĺ: Ôāó –į) f(—Ö1) < f(—Ö2) , —ā–ĺ —Ą—É–Ĺ–ļ—Ü—Ė—Ź –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –∑—Ä–ĺ—Ā—ā–į—é—á–ĺ—é; Ôāó –Ī) f(—Ö1) > f(—Ö2), —Ą—É–Ĺ–ļ—Ü—Ė—Ź –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź —Ā–Ņ–į–ī–Ĺ–ĺ—é.
- 12. –ü–į—Ä–Ĺ—Ė —ā–į –Ĺ–Ķ–Ņ–į—Ä–Ĺ—Ė —Ą—É–Ĺ–ļ—Ü—Ė—ó. –ě–∑–Ĺ. 8: –Ě–Ķ—Ö–į–Ļ —Ą—É–Ĺ–ļ—Ü—Ė—Ź f(—Ö) –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–į –Ĺ–į –ľ–Ĺ–ĺ–∂–ł–Ĺ—Ė –ź. –§—É–Ĺ–ļ—Ü—Ė—é f(—Ö) –Ĺ–į–∑–ł–≤–į—é—ā—Ć –Ņ–į—Ä–Ĺ–ĺ—é, —Ź–ļ—Č–ĺ f(‚Äď—Ö)= f(—Ö), —Ė –Ĺ–Ķ–Ņ–į—Ä–Ĺ–ĺ—é, —Ź–ļ—Č–ĺ f(‚Äď—Ö)=‚Äď f(—Ö). –ď—Ä–į—Ą—Ė–ļ –Ņ–į—Ä–Ĺ–ĺ—ó —Ą—É–Ĺ–ļ—Ü—Ė—ó —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł–Ļ –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ĺ—Ā—Ė –ě—É, –į –Ĺ–Ķ–Ņ–į—Ä–Ĺ–ĺ—ó ‚Äď –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –Ņ–ĺ—á–į—ā–ļ—É –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā.
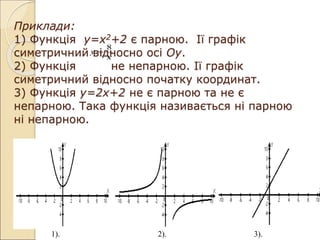
- 13. –ü—Ä–ł–ļ–Ľ–į–ī–ł: 1) –§—É–Ĺ–ļ—Ü—Ė—Ź —É=—Ö2+2 —Ē –Ņ–į—Ä–Ĺ–ĺ—é. –Ü—ó –≥—Ä–į—Ą—Ė–ļ —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł–Ļ –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ĺ—Ā—Ė –ě—É. 2) –§—É–Ĺ–ļ—Ü—Ė—Ź –Ĺ–Ķ –Ĺ–Ķ–Ņ–į—Ä–Ĺ–ĺ—é. –Ü—ó –≥—Ä–į—Ą—Ė–ļ —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł–Ļ –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –Ņ–ĺ—á–į—ā–ļ—É –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. 3) –§—É–Ĺ–ļ—Ü—Ė—Ź —É=2—Ö+2 –Ĺ–Ķ —Ē –Ņ–į—Ä–Ĺ–ĺ—é —ā–į –Ĺ–Ķ —Ē –Ĺ–Ķ–Ņ–į—Ä–Ĺ–ĺ—é. –Ę–į–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė—Ź –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ĺ—Ė –Ņ–į—Ä–Ĺ–ĺ—é –Ĺ—Ė –Ĺ–Ķ–Ņ–į—Ä–Ĺ–ĺ—é. —Ö —É 8 ÔÄĹ 1). 2). 3).
- 14. –ü–Ķ—Ä—Ė–ĺ–ī–ł—á–Ĺ—Ė —Ą—É–Ĺ–ļ—Ü—Ė—ó. –ě–∑–Ĺ. 9: –§—É–Ĺ–ļ—Ü—Ė—Ź f(—Ö), –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–į –Ĺ–į –≤—Ā—Ė–Ļ —á–ł—Ā–Ľ–ĺ–≤—Ė–Ļ –Ņ—Ä—Ź–ľ—Ė–Ļ, –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ņ–Ķ—Ä—Ė–ĺ–ī–ł—á–Ĺ–ĺ—é, —Ź–ļ—Č–ĺ —Ė—Ā–Ĺ—É—Ē —ā–į–ļ–Ķ —á–ł—Ā–Ľ–ĺ –Ę, —Č–ĺ f(—Ö+–Ę)= f(—Ö). –ß–ł—Ā–Ľ–ĺ –Ę –Ĺ–į–∑–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ņ–Ķ—Ä—Ė–ĺ–ī–ĺ–ľ —Ą—É–Ĺ–ļ—Ü—Ė—ó. –Į–ļ—Č–ĺ –Ę ‚Äď –Ņ–Ķ—Ä—Ė–ĺ–ī —Ą—É–Ĺ–ļ—Ü—Ė—ó, —ā–ĺ —ó—ó –Ņ–Ķ—Ä—Ė–ĺ–ī–į–ľ–ł —Ē —ā–į–ļ–ĺ–∂ —á–ł—Ā–Ľ–į –ļ–Ę, –ī–Ķ –ļ —Ē Z.
- 15. –ü–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė–Ļ 1. –ď—Ä–į—Ą—Ė–ļ —Ą—É–Ĺ–ļ—Ü—Ė—ó y=f(x)+b –ĺ—ā—Ä–ł–ľ—É—Ē–ľ–ĺ –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł–ľ –Ņ–Ķ—Ä–Ķ–Ĺ–Ķ—Ā–Ķ–Ĺ–Ĺ—Ź–ľ –≤–∑–ī–ĺ–≤–∂ –ĺ—Ā—Ė –ě—É –Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ—É, —Č–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē b.
- 16. –ü–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė–Ļ 2. –ď—Ä–į—Ą—Ė–ļ —Ą—É–Ĺ–ļ—Ü—Ė—ó y=f(x+–į) –ĺ—ā—Ä–ł–ľ—É—Ē–ľ–ĺ –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ–ł–ľ –Ņ–Ķ—Ä–Ķ–Ĺ–Ķ—Ā–Ķ–Ĺ–Ĺ—Ź–ľ –≤–∑–ī–ĺ–≤–∂ –ĺ—Ā—Ė –ě—Ö –Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ—É, —Č–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –į.
- 17. –ü–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė–Ļ 3. –ď—Ä–į—Ą—Ė–ļ —Ą—É–Ĺ–ļ—Ü—Ė—ó, –ĺ—ā—Ä–ł–ľ—É—Ē–ľ–ĺ –∑ –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė—ó –Ņ—Ä–ł 0<—Ā<1 –∑–į –ī–ĺ–Ņ–ĺ–ľ–ĺ–≥–ĺ—é —Ā—ā–ł—Ā–ļ—É–≤–į–Ĺ–Ĺ—Ź –≤ —Ä–į–∑—Ė–≤ –ĺ—Ä–ī–ł–Ĺ–į—ā –ĺ—Ā—ā–į–Ĺ–Ĺ—Ć–ĺ–≥–ĺ, –į –Ņ—Ä–ł —Ā>1 –∑–į –ī–ĺ–Ņ–ĺ–ľ–ĺ–≥–ĺ—é —Ä–ĺ–∑—ā—Ź–≥—É–≤–į–Ĺ–Ĺ—Ź –≤ —Ā —Ä–į–∑—Ė–≤ –Ļ–ĺ–≥–ĺ –ĺ—Ä–ī–ł–Ĺ–į—ā —Ė–∑ –∑–Ī–Ķ—Ä–Ķ–∂–Ķ–Ĺ–Ĺ—Ź–ľ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ł—Ö –į–Ī—Ā—Ü–ł—Ā.
- 18. –ü–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė–Ļ 4. –ď—Ä–į—Ą—Ė–ļ —Ą—É–Ĺ–ļ—Ü—Ė—ó , –ī—Ė—Ā—ā–į—Ē–ľ–ĺ –∑ –≥—Ä–į—Ą—Ė–ļ–į —Ą—É–Ĺ–ļ—Ü—Ė—ó –Ņ—Ä–ł 0<k<1 –∑–į –ī–ĺ–Ņ–ĺ–ľ–ĺ–≥–ĺ—é –∑–Ī—Ė–Ľ—Ć—ą–Ķ–Ĺ–Ĺ—Ź–ľ –≤ —Ä–į–∑—Ė–≤ –į–Ī—Ā—Ü–ł—Ā –Ļ–ĺ–≥–ĺ —ā–ĺ—á–ĺ–ļ, –į –Ņ—Ä–ł k>1 –∑–ľ–Ķ–Ĺ—ą–Ķ–Ĺ–Ĺ—Ź–ľ –≤ k —Ä–į–∑—Ė–≤ –į–Ī—Ā—Ü–ł—Ā –Ļ–ĺ–≥–ĺ —ā–ĺ—á–ĺ–ļ —Ė–∑ –∑–Ī–Ķ—Ä–Ķ–∂–Ķ–Ĺ–Ĺ—Ź–ľ —ó—Ö–Ĺ—Ė—Ö –ĺ—Ä–ī–ł–Ĺ–į—ā.
- 19. –ü—Ä–ł–ļ–Ľ–į–ī: –ö–ĺ—Ä–ł—Ā—ā—É—é—á–ł—Ā—Ć –≥—Ä–į—Ą—Ė–ļ–ĺ–ľ —Ą—É–Ĺ–ļ—Ü—Ė—ó —É=—Ö2, –Ņ–ĺ–Ī—É–ī—É–≤–į—ā–ł –≥—Ä–į—Ą—Ė–ļ —Ą—É–Ĺ–ļ—Ü—Ė—ó —É=(—Ö+1)2+2. .