连立方程式の解き方?线形代数とグレブナー基底?
- 2. 自己紹介 ? グレブナー基底が大好きなbot ? ツイートはすべて手動 ? グレブナー基底についてツイート することでグレブナー基底を普及する bot ? 数学ラノベ「最近、妹がグレブナー基底 に興味を持ち始めたのだが。」(数理学院 出版)の著者 ? 「グレブナー基底にはポン酢が合う」の生みの親 グレブナー基底大好きbotとは?
- 4. 連立方程式を解く ? 加減法 (1)を2倍して(2)を引く。つまり、(1)×2-(2) を計算。 よって、 を(1)に代入して、 答えは、
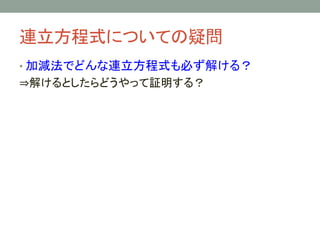
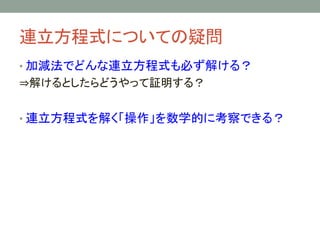
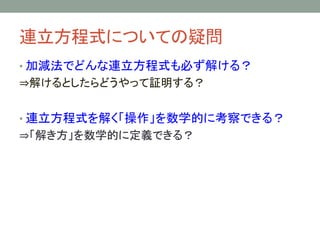
- 8. 連立方程式についての疑問 ? 加減法でどんな連立方程式も必ず解ける? ?解けるとしたらどうやって証明する? ? 連立方程式を解く「操作」を数学的に考察できる? ?「解き方」を数学的に定義できる?
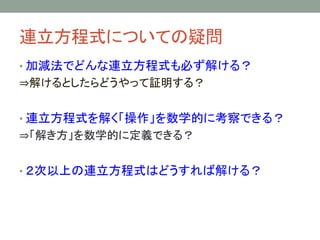
- 9. 連立方程式についての疑問 ? 加減法でどんな連立方程式も必ず解ける? ?解けるとしたらどうやって証明する? ? 連立方程式を解く「操作」を数学的に考察できる? ?「解き方」を数学的に定義できる? ? 2次以上の连立方程式はどうすれば解ける?
- 10. 連立方程式についての疑問 ? 加減法でどんな連立方程式も必ず解ける? ?解けるとしたらどうやって証明する? ? 連立方程式を解く「操作」を数学的に考察できる? ?「解き方」を数学的に定義できる? ? 2次以上の连立方程式はどうすれば解ける? ? はどうやって解く?
- 11. 連立方程式についての疑問 ? 加減法でどんな連立方程式も必ず解ける? ?解けるとしたらどうやって証明する? ? 連立方程式を解く「操作」を数学的に考察できる? ?「解き方」を数学的に定義できる? ? 2次以上の连立方程式はどうすれば解ける? ? はどうやって解く? 線形代数 グレブナー基底
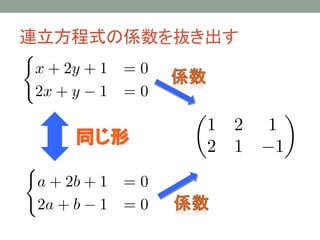
- 12. 连立方程式の係数を抜き出す
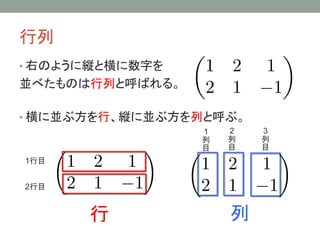
- 14. 色々な行列
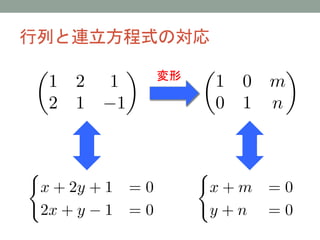
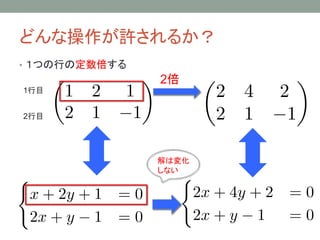
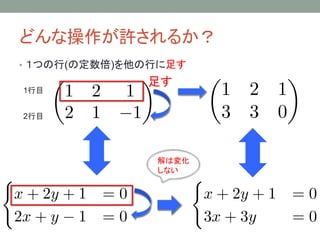
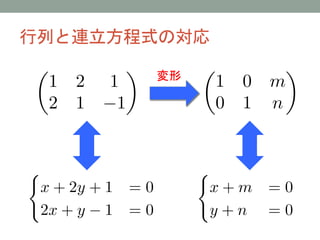
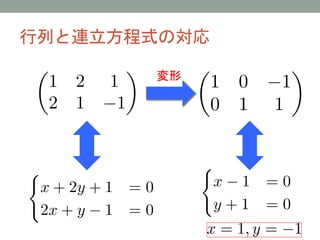
- 16. 行列と連立方程式の対応 変形
- 19. 行列と連立方程式の対応 変形
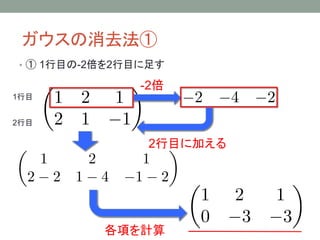
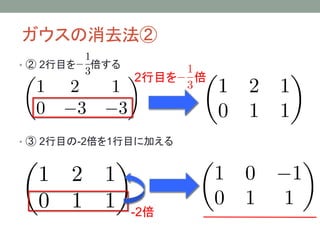
- 21. ガウスの消去法② ? ② 2行目を 倍する ? ③ 2行目の-2倍を1行目に加える 2行目を 倍 -2倍
- 22. 行列と連立方程式の対応 変形
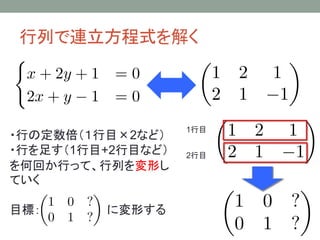
- 23. 連立方程式と行列 ? 連立方程式を行列で表した ?係数を行と列に並べる ? 連立方程式を解く操作は、行の操作(行基本変形)に対応す る ?行を定数倍する、行を足す操作は加減法に対応している ? 行基本変形で(線形)連立方程式が解けることは数学的に証 明できる ? 「線形代数」では、行列の様々な計算について考察する
- 26. 連立方程式の重要性 ? 解が有限個とは限らない連立方程式も考えられる。 これらは代数幾何学の言葉で代数多様体(アフィン多様体)と 呼ばれる。 多くの数学者によって、代数多様体は研究されてきている。
- 27. 数学とコンピュータ ? 行列の計算やグレブナー基底はコンピュータで計算すること ができる ? 行列は純粋数学以外にも、人工知能や暗号理論にも用いら れる ? 近年ではコンピュータを用いた数学の研究も盛んになってきて いる
- 28. まとめ ? 連立方程式は行列を使って解くことができる ? 行列は線形代数において重要な概念である ? 連立方程式は代数幾何学などで扱われる ? 次数が大きい連立方程式はグレブナー基底を使って解ける