Stadium Evacuation
- 1. Evacuation of UNL Memorial Stadium Sunil Gyawali & Adrian Lara
- 2. Introductrivia • Population of Omaha? 408,958 • Population of Lincoln? 258,379 • Population of Bellevue? 50,137 • Capacity of UNL Memorial Stadium? 91,000 It is true that Memorial Stadium is the 3rd most crowded city in Nebraska! …. How long does it take to evacuate?
- 3. Problem and assumptions • Problem: Time to evacuate the fans from Memorial Stadium at full capacity? • Assumptions: • The stadium is full • Leave stadium=Out of the system
- 4. Objectives • To model the UNL Memorial Stadium as a queueing system • To compare the observed results with other simulation processes • To discuss if the simulation times obtained are compliant with current evacuation regulation
- 5. Data collection and assumptions (1) 148 blocks in total 91,000 fans => 615 fans per block 33 blocks, 7 gates 33 * 615 = 20295 fans 20295/7 = 2900 fans per gate Assumed capacity: 91,000 fans
- 6. Data collection and assumptions (2) Side #Blocks Estimated #fans Gates Estimated population gate South 31 19065 4 4767 North 33 20295 5 4059 East 33 20295 7 2900 West 51 31365 4 7842 Table 1: Estimated population per gate. per
- 7. Data collection and assumptions (3) Population = 4059/Gates Population = 4767/Gates GATES: 24,1,2,3 Population =2900/Gates = GATES: 4,6,8,10 Population= 7842/Gates GATES: 11,12,14,15,16 GATES:17,18,19, 20,21,22,23 The big picture of how our queues look like
- 8. Data collection and analysis (4) • How many fans arrive at a gate per minute: • Uniform between 200 and 300 per minute • How many fans exit a gate per minute: • Constant 180 per minute • Transfer time from seat to gate: • Uniform between 1 and 10 minutes Note: Observations were done on November 9th, Huskers vs Wolverines. Does this look like an emergency evacuation? (Hint: how did we win that match? )
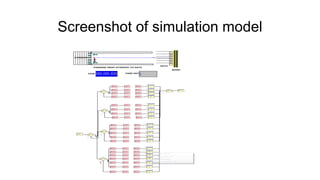
- 9. Arena model construction • We have 20 of these: • Max arrival is different for each gate (based on population) • Arrival rate, service rate and transfer time are the same for each queue Time for Arena demo!!!!!
- 10. Screenshot of simulation model
- 11. Results Simulation of each side of the stadium Sides South West North East Total Population Numer of gates Number of servers 4767 7842 4059 2900 4 4 5 7 6 6 6 6 Arrival rate Service rate Simulation time (minutes) Uniform (0.2,0.3) seconds Uniform (0.2,0.3) seconds Uniform (0.2,0.3) seconds Uniform (0.2,0.3) seconds Constant (2 s) Constant (2 s) Constant (2 s) Constant (2 s) 30.883 47.967 26.950 21.850 Arrival rate Service rate per server Simulation time (minutes) Uniform (0.01.0.015) seconds Constant (2 s) 48.4 Complete simulation Gate All Total Poulation Number of gates Number of servers 91031 20 20*6 Evacuation Time
- 12. Validation Direct Estimation: Highest Population = 7842 (west Gate) Service Rate = 30 minute *6 /fan Total time for serving fan = 7842/180= 43.57 minutes Considering walk time = 5.5 minutes (Uniform (1,10)) Total Time for evacuation = 43.57+5.5 = 49.57 minutes Simulated evacuation time = 48.4 minutes Percentage Error = (48.54-49.57)/49.57 = -2.08 %
- 13. Conclusions • We found that: • The evacuation time obtained from the simulation is 48 minute and 25 second • The simulation result matches the estimation. • Accomplishment of objectives: • To model the UNL Memorial Stadium as a queueing system: Done! • To compare the observed results with other simulation processes: Next week! • To discuss if the simulation times obtained are compliant with current evacuation regulation: Next week!
- 14. Thank you!