1 of 15
Download to read offline





Ad
Recommended
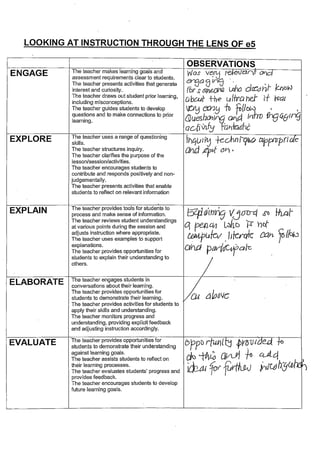
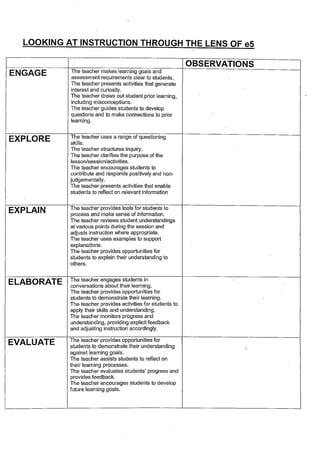
e5 Ultranet PD Observations - Assessment
e5 Ultranet PD Observations - Assessmentcoburgmaths
╠²
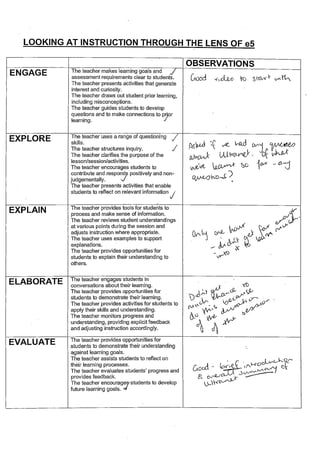
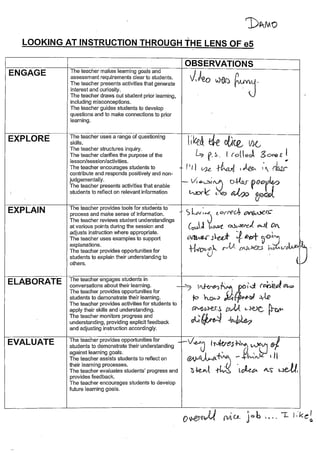
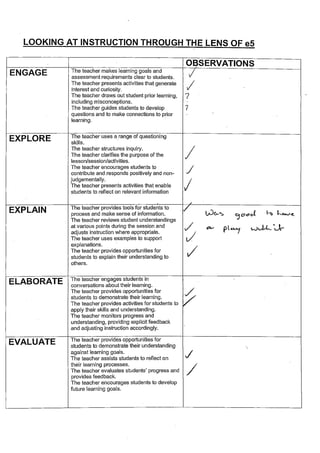
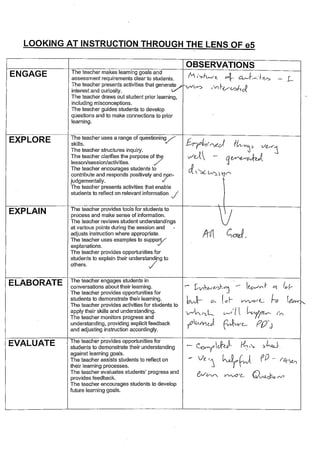
Staff assessed a PD Vanaja and I delivered on the UltranetCAS Instructions
CAS Instructionscoburgmaths
╠²
1) The document provides instructions for using the basic features and applications of the TI-nspire CAS calculator, including the calculator, graphing, geometry, lists and spreadsheet, notes, and data analysis applications.
2) Key functions and menus are demonstrated for drawing graphs and shapes, performing calculations and regressions, and moving between applications.
3) Examples show how to enter and manipulate equations, tables, text, and geometric objects, as well as perform statistical analysis and regressions using the built-in data tools.Ultranet booklet session 2
Ultranet booklet session 2coburgmaths
╠²
This document describes the features of an online platform called Ultranet, including a personalized home page for all users, an express page for personal space, a collaborative space for student learning and work, a community space, a professional development space for teachers, and a content storage and search area called "My content".Linear equations part i
Linear equations part icoburgmaths
╠²
The document discusses linear equations and graphing lines. It covers plotting points, calculating slope, writing equations in slope-intercept form, and graphing lines by making a table or using the slope and y-intercept. Methods are presented for finding the equation of a line given two points, the slope and a point, or from a graph.Sam maths pres
Sam maths prescoburgmaths
╠²
The document discusses various types of transformations that can be performed on the graph of the function f(x)=logax. It explains that dilations on the x-axis are shown by coefficients in front of x in the equation, dilations on the y-axis by coefficients in front of the log term. Translations are shown by adding or subtracting terms from x or at the end of the equation for x-axis or y-axis translations respectively. Reflections are shown by changing the sign in front of terms or dividing the entire equation by 1. It also discusses finding degrees from radians and vice versa, finding intercepts of log equations, and determining the composition of two functions.Wedderburn College Newsletter 28th March 2012
Wedderburn College Newsletter 28th March 2012coburgmaths
╠²
The document provides information about upcoming parent-teacher-student interviews at Wedderburn College in Victoria, Australia. It discusses that the interviews will take place on March 29th in Wedderburn and March 28th in Inglewood to discuss student learning. It also mentions several other events happening at the end of the term like a casual day fundraiser and working bees planned for the start of next term.2011 Whole School Action Plan Curriculum PD Presentation
2011 Whole School Action Plan Curriculum PD Presentationcoburgmaths
╠²
This document outlines a curriculum professional development session focused on developing a whole school action plan. Key points discussed include:
- The session focused on improving understanding of the e5 framework and identifying different types of questioning.
- A whole school action plan was proposed to improve student learning outcomes through a collaborative approach focusing on areas like learning intentions, feedback, and higher-order questioning.
- Data was presented indicating the need for improvement, and professional learning teams would be formed to design inquiries around addressing this need through collaborative learning and feedback cycles.Ultranet booklet
Ultranet bookletcoburgmaths
╠²
This document describes the features of an online platform called Ultranet, including a personalized home page for all users, an express page for personal space, a collaborative space for student learning and work, a community space, a professional development space for teachers, and a content storage and search area called "My content".Multi modal think board placemat
Multi modal think board placematcoburgmaths
╠²
This document discusses a multi-modal approach to teaching mathematics that involves exploring, engaging, explaining, elaborating and evaluating using different modes such as numbers, words, stories, real-life examples, symbols, diagrams, and thinking mathematically. It focuses on using calculation, communication, application, manipulation, visualization and strategies to teach mathematical concepts in a technological age.Multi modal think board details
Multi modal think board detailscoburgmaths
╠²
This document discusses using a multi-modal think board approach to teach mathematics. It involves using concrete manipulatives, diagrams, illustrations, pictures, charts and graphs to develop students' mental models and understanding of abstract mathematical concepts. Students learn by doing physical activities, making demonstrations, and using manipulatives like paper, cubes and tiles. Diagrams vary in abstraction from literal pictures to representations using dots. They convey ideas vividly. The multi-modal think board can be used for lesson planning, assessment, integrating technology, and reflecting on student and teacher learning.Thinking and working mathematically
Thinking and working mathematically coburgmaths
╠²
The document discusses using a multi-modal think board approach to teaching mathematics. It describes the six mathematical modes of thinking - number, word, diagram, symbol, real thing, and story. Examples are provided of how to differentiate mathematics instruction for students using open-ended questions within these six modes. The goal is to engage students in thinking and working mathematically in a variety of ways.Kim Solving
Kim Solvingcoburgmaths
╠²
This document provides instructions on how to solve various types of equations, including:
- Linear equations by rearranging to isolate the variable
- Equations using the null factor law to find zeros
- Exponential and logarithmic equations by equating exponents or rearranging into logarithmic form
- Logarithmic functions using properties of logarithms
- Using the "solve" command to solve equations on a calculator
- Circular function equations by rearranging to isolate the variable
It also provides examples and exercises to practice these techniques.Kim Modelling Functions
Kim Modelling Functionscoburgmaths
╠²
The document discusses different types of modeling involving functions. It provides examples of exponential, logarithmic, and circular functions where the variables or constants are missing and points on the graphs are given. Readers are instructed to find the values of the missing variables or constants by inserting the points into the corresponding function equations. Exercises from the textbook are assigned for practice.Aleesha guide to evaluating and converting
Aleesha guide to evaluating and convertingcoburgmaths
╠²
This document provides guidance on evaluating and converting between radians and degrees.
It defines conversion as changing the form of a quantity without changing its value. The angle in radians swept out in one revolution of a circle is 2ŽĆ radians (where ŽĆ radians = 180 degrees).
When converting between radians and degrees, the formula 1 degree = ŽĆ/180 radians is used. For example, to convert 30 degrees to radians, 30 ├Ś ŽĆ/180 = ŽĆ/6 radians.
Evaluation is defined as calculating the numerical value of an expression. Trigonometric functions are evaluated on the unit circle, where P(╬Ė) = (cos╬Ė, sin╬Ė) and symmetry properties allow determining values in eachSample Choc Chip Simulation Report Writing
Sample Choc Chip Simulation Report Writingcoburgmaths
╠²
1. The simulation involved modeling the making of chocolate chip cookies with a random number of chips in each cookie. Data was collected from 5 batches of 10 cookies each to determine the average number of chips used.
2. On average, 88.8 chips were needed per batch, with 19 chips wasted on average since the goal was 7 chips per cookie. Each cookie ended up having an average of 9 chips.
3. The simulation could have used a deck of cards instead of a calculator to generate random numbers by removing some cards and flipping them over randomly. This would allow modeling different chip requirements like 6 chips per cookie.Mathsmate Glossary
Mathsmate Glossarycoburgmaths
╠²
- The glossary defines key mathematical terms like accuracy, acute angle, addition, algebra, area, ascending order, and more.
- Definitions provide the meaning of each term along with visual examples to illustrate concepts like acute triangles, adjacent angles, and alternate interior angles.
- The glossary acts as a reference for mathematical vocabulary, concepts, properties, and notations.Stationary Points Handout
Stationary Points Handoutcoburgmaths
╠²
There are three types of stationary points: maximum points, minimum points, and points of inflection. A maximum point occurs when the gradient is positive on one side and negative on the other. A minimum point occurs when the gradient is negative on one side and positive on the other. A point of inflection occurs when the gradient is zero but the second derivative is also zero. To determine the type of stationary point, the gradient on each side is considered and the second derivative at that point is examined. Sketching the curve involves finding any stationary points, where the curve meets the axes, and using the information to plot the general shape.Equations of Tangents and Normals
Equations of Tangents and Normalscoburgmaths
╠²
This document provides questions about finding the equations of tangents and normals to various polynomial functions at given points. It contains 8 parts with multiple questions each about finding the equations of tangents to polynomial curves and normals to polynomial curves at specified points using differentiation.Differentiation of Polynomials Questions
Differentiation of Polynomials Questionscoburgmaths
╠²
This document provides 30 problems involving differentiating polynomials, where the task is to find the derivative (dy/dx) of each given polynomial function y=f(x). The polynomials range in degree from 1 to 4 and include both standard and fractional exponent terms. The problems are presented systematically to comprehensively cover the basic differentiation rules for polynomials.More Related Content
More from coburgmaths (20)
2011 Whole School Action Plan Curriculum PD Presentation
2011 Whole School Action Plan Curriculum PD Presentationcoburgmaths
╠²
This document outlines a curriculum professional development session focused on developing a whole school action plan. Key points discussed include:
- The session focused on improving understanding of the e5 framework and identifying different types of questioning.
- A whole school action plan was proposed to improve student learning outcomes through a collaborative approach focusing on areas like learning intentions, feedback, and higher-order questioning.
- Data was presented indicating the need for improvement, and professional learning teams would be formed to design inquiries around addressing this need through collaborative learning and feedback cycles.Ultranet booklet
Ultranet bookletcoburgmaths
╠²
This document describes the features of an online platform called Ultranet, including a personalized home page for all users, an express page for personal space, a collaborative space for student learning and work, a community space, a professional development space for teachers, and a content storage and search area called "My content".Multi modal think board placemat
Multi modal think board placematcoburgmaths
╠²
This document discusses a multi-modal approach to teaching mathematics that involves exploring, engaging, explaining, elaborating and evaluating using different modes such as numbers, words, stories, real-life examples, symbols, diagrams, and thinking mathematically. It focuses on using calculation, communication, application, manipulation, visualization and strategies to teach mathematical concepts in a technological age.Multi modal think board details
Multi modal think board detailscoburgmaths
╠²
This document discusses using a multi-modal think board approach to teach mathematics. It involves using concrete manipulatives, diagrams, illustrations, pictures, charts and graphs to develop students' mental models and understanding of abstract mathematical concepts. Students learn by doing physical activities, making demonstrations, and using manipulatives like paper, cubes and tiles. Diagrams vary in abstraction from literal pictures to representations using dots. They convey ideas vividly. The multi-modal think board can be used for lesson planning, assessment, integrating technology, and reflecting on student and teacher learning.Thinking and working mathematically
Thinking and working mathematically coburgmaths
╠²
The document discusses using a multi-modal think board approach to teaching mathematics. It describes the six mathematical modes of thinking - number, word, diagram, symbol, real thing, and story. Examples are provided of how to differentiate mathematics instruction for students using open-ended questions within these six modes. The goal is to engage students in thinking and working mathematically in a variety of ways.Kim Solving
Kim Solvingcoburgmaths
╠²
This document provides instructions on how to solve various types of equations, including:
- Linear equations by rearranging to isolate the variable
- Equations using the null factor law to find zeros
- Exponential and logarithmic equations by equating exponents or rearranging into logarithmic form
- Logarithmic functions using properties of logarithms
- Using the "solve" command to solve equations on a calculator
- Circular function equations by rearranging to isolate the variable
It also provides examples and exercises to practice these techniques.Kim Modelling Functions
Kim Modelling Functionscoburgmaths
╠²
The document discusses different types of modeling involving functions. It provides examples of exponential, logarithmic, and circular functions where the variables or constants are missing and points on the graphs are given. Readers are instructed to find the values of the missing variables or constants by inserting the points into the corresponding function equations. Exercises from the textbook are assigned for practice.Aleesha guide to evaluating and converting
Aleesha guide to evaluating and convertingcoburgmaths
╠²
This document provides guidance on evaluating and converting between radians and degrees.
It defines conversion as changing the form of a quantity without changing its value. The angle in radians swept out in one revolution of a circle is 2ŽĆ radians (where ŽĆ radians = 180 degrees).
When converting between radians and degrees, the formula 1 degree = ŽĆ/180 radians is used. For example, to convert 30 degrees to radians, 30 ├Ś ŽĆ/180 = ŽĆ/6 radians.
Evaluation is defined as calculating the numerical value of an expression. Trigonometric functions are evaluated on the unit circle, where P(╬Ė) = (cos╬Ė, sin╬Ė) and symmetry properties allow determining values in eachSample Choc Chip Simulation Report Writing
Sample Choc Chip Simulation Report Writingcoburgmaths
╠²
1. The simulation involved modeling the making of chocolate chip cookies with a random number of chips in each cookie. Data was collected from 5 batches of 10 cookies each to determine the average number of chips used.
2. On average, 88.8 chips were needed per batch, with 19 chips wasted on average since the goal was 7 chips per cookie. Each cookie ended up having an average of 9 chips.
3. The simulation could have used a deck of cards instead of a calculator to generate random numbers by removing some cards and flipping them over randomly. This would allow modeling different chip requirements like 6 chips per cookie.Mathsmate Glossary
Mathsmate Glossarycoburgmaths
╠²
- The glossary defines key mathematical terms like accuracy, acute angle, addition, algebra, area, ascending order, and more.
- Definitions provide the meaning of each term along with visual examples to illustrate concepts like acute triangles, adjacent angles, and alternate interior angles.
- The glossary acts as a reference for mathematical vocabulary, concepts, properties, and notations.Stationary Points Handout
Stationary Points Handoutcoburgmaths
╠²
There are three types of stationary points: maximum points, minimum points, and points of inflection. A maximum point occurs when the gradient is positive on one side and negative on the other. A minimum point occurs when the gradient is negative on one side and positive on the other. A point of inflection occurs when the gradient is zero but the second derivative is also zero. To determine the type of stationary point, the gradient on each side is considered and the second derivative at that point is examined. Sketching the curve involves finding any stationary points, where the curve meets the axes, and using the information to plot the general shape.Equations of Tangents and Normals
Equations of Tangents and Normalscoburgmaths
╠²
This document provides questions about finding the equations of tangents and normals to various polynomial functions at given points. It contains 8 parts with multiple questions each about finding the equations of tangents to polynomial curves and normals to polynomial curves at specified points using differentiation.Differentiation of Polynomials Questions
Differentiation of Polynomials Questionscoburgmaths
╠²
This document provides 30 problems involving differentiating polynomials, where the task is to find the derivative (dy/dx) of each given polynomial function y=f(x). The polynomials range in degree from 1 to 4 and include both standard and fractional exponent terms. The problems are presented systematically to comprehensively cover the basic differentiation rules for polynomials.