Statistics and big data for justice and fairness
- 1. Statistics for justice and fairness ÓĖ£ÓĖ©.ÓĖöÓĖŻ.ÓĖŁÓĖ▓ÓĖÖÓĖÖÓĖŚÓ╣ī ÓĖ©ÓĖ▒ÓĖüÓĖöÓĖ┤Ó╣īÓĖ¦ÓĖŻÓĖ¦ÓĖ┤ÓĖŖÓĖŹÓ╣ī ÓĖ£ÓĖ╣Ó╣ēÓĖŁÓĖ▓ÓĖÖÓĖ¦ÓĖóÓĖüÓĖ▓ÓĖŻÓĖ½ÓĖźÓĖ▒ÓĖüÓĖ¬ÓĖ╣ÓĖĢÓĖŻ Ph.D. and M.Sc. in Business Analytics and Data Science ÓĖŁÓĖ▓ÓĖłÓĖ▓ÓĖŻÓĖóÓ╣īÓĖøÓĖŻÓĖ░ÓĖłÓĖ▓ÓĖ¬ÓĖ▓ÓĖéÓĖ▓ÓĖ¦ÓĖ┤ÓĖŖÓĖ▓ÓĖ¦ÓĖ┤ÓĖŚÓĖóÓĖ▓ÓĖüÓĖ▓ÓĖŻÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖĀÓĖ▒ÓĖóÓ╣üÓĖźÓĖ░ÓĖüÓĖ▓ÓĖŻÓĖÜÓĖŻÓĖ┤ÓĖ½ÓĖ▓ÓĖŻÓĖäÓĖ¦ÓĖ▓ÓĖĪÓ╣ĆÓĖ¬ÓĖĄÓ╣łÓĖóÓĖć ÓĖäÓĖōÓĖ░ÓĖ¬ÓĖ¢ÓĖ┤ÓĖĢÓĖ┤ÓĖøÓĖŻÓĖ░ÓĖóÓĖĖÓĖüÓĖĢÓ╣ī ÓĖ¬ÓĖ¢ÓĖ▓ÓĖÜÓĖ▒ÓĖÖÓĖÜÓĖ▒ÓĖōÓĖæÓĖ┤ÓĖĢÓĖ×ÓĖ▒ÓĖÆÓĖÖÓĖÜÓĖŻÓĖ┤ÓĖ½ÓĖ▓ÓĖŻÓĖ©ÓĖ▓ÓĖ¬ÓĖĢÓĖŻÓ╣ī
- 6. Roles of statistics in fairness and justice ŌĆó Facilitate fairness ŌĆó Detect anomaly and fraud ŌĆó Prevent crime and anomaly ŌĆó Regulatory Impact Assessment
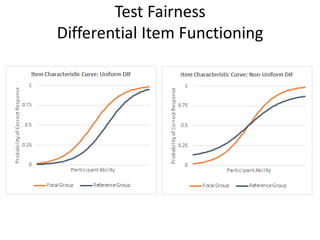
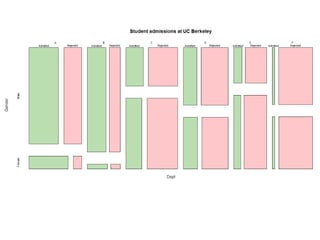
- 8. Test Fairness Differential Item Functioning
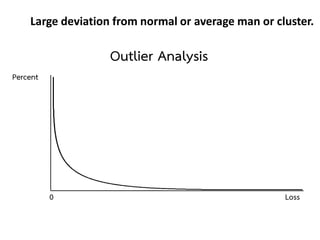
- 15. There is no crime without any trace! -Large deviation from normal or average man or cluster. -Large deviation from past behavior. -Inconsistency with themselves and surroundings. -Repeated anomaly pattern. -Caution on statistical detection of cheating and anomalous detection Anomaly Detection
- 16. Outlier Analysis 0 Percent Loss Large deviation from normal or average man or cluster.
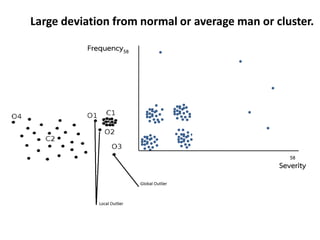
- 17. Large deviation from normal or average man or cluster. v 58 Severity Frequency58
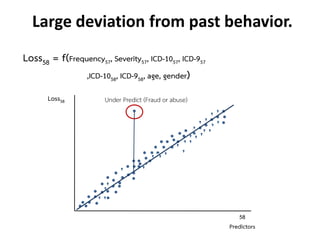
- 18. Loss58 = f(Frequency57, Severity57, ICD-1057, ICD-957 ,ICD-1058, ICD-958, age, gender) Loss58 58 Predictors Under Predict (Fraud or abuse) v vvvvv vvvvv vvvvv vv vv v v vv v vv Large deviation from past behavior.
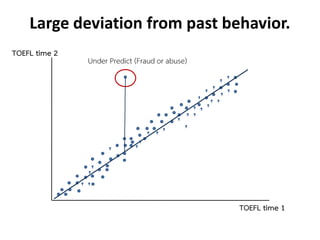
- 19. Large deviation from past behavior. TOEFL time 2 TOEFL time 1 Under Predict (Fraud or abuse) v v vv vv vv vvv vv vvv vv vv v v vv v v v
- 20. Inconsistency with themselves and surroundings. -Low ability test taker can answer difficult item. -K-index for copying! Eight dimensions -Scoring test with contaminated response vector -Influence function + Robust estimators
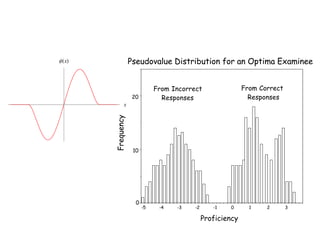
- 22. -5 -4 -3 -2 -1 0 1 2 3 0 10 20 Pseudovalue Distribution for an Optima Examinee Proficiency Estimaate Frequency From Incorrect Responses From Correct Responses
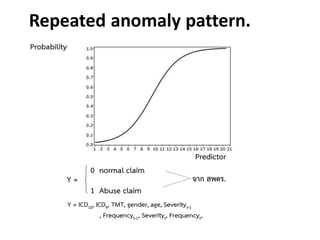
- 24. Repeated anomaly pattern. Predictor Probability Y = 0 normal claim 1 Abuse claim ÓĖłÓĖ▓ÓĖü ÓĖ¬ÓĖ×ÓĖĢÓĖŻ. Y = ICD10, ICD9, TMT, gender, age, Severityt-1 , Frequencyt-1, Severityt, Frequencyt,
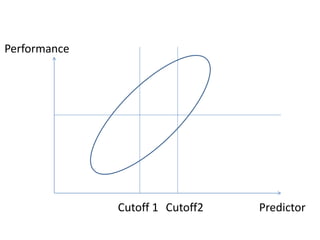
- 25. Caution on statistical detection of cheating
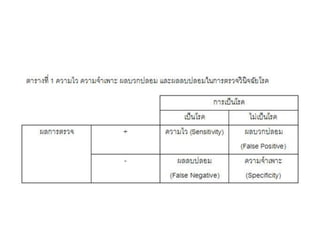
- 28. ŌĆó Positive Predictive Value: PPV Caution on statistical detection of cheating 64.76 % 99.30%
- 29. ŌĆó Statistical evidence as a red flag or warning ŌĆó Physical evidence is always needed. ŌĆó Early detection, protection, and prevention. ŌĆó Bayesian flip is needed. Caution on statistical detection of cheating P(Cheating=Yes|Detection=Yes) P(Detection=Yes|Cheating=Yes) P(Cheating=No|Detection=No) P(Detection=No|Cheating=No) P(Cheating=Yes|Detection=Yes)=P(Detection=Yes|Cheating=Yes)*P(Cheating=Yes) P(Detection=Yes)
- 30. ÓĖüÓĖ▓ÓĖŻÓĖ¬ÓĖŻÓ╣ēÓĖ▓ÓĖćÓ╣üÓĖÜÓĖÜÓĖłÓĖ▓ÓĖźÓĖŁÓĖćÓĖŻÓĖ▓ÓĖóÓĖüÓĖ▓ÓĖŻÓĖŖÓĖ▓ÓĖŻÓĖ░Ó╣ĆÓĖćÓĖ┤ÓĖÖÓĖ£ÓĖ┤ÓĖöÓĖøÓĖüÓĖĢÓĖ┤ÓĖéÓĖŁÓĖć ÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓ╣éÓĖöÓĖóÓĖüÓĖ▓ÓĖŻÓ╣āÓĖŖÓ╣ēÓ╣ĆÓĖŚÓĖäÓĖÖÓĖ┤ÓĖä Local Outlier Factor(LOF) ÓĖøÓĖ▒ÓĖōÓĖōÓĖ¦ÓĖ┤ÓĖŖÓĖŹÓ╣ī ÓĖ¦ÓĖ┤ÓĖ©ÓĖ▒ÓĖźÓĖóÓĖ▓ÓĖ¦ÓĖ▒ÓĖÆÓĖ╚©╣īÓ╣ī
- 32. ÓĖüÓĖ▓ÓĖŻÓĖ¤ÓĖŁÓĖüÓ╣ĆÓĖćÓĖ┤ÓĖÖÓ╣āÓĖÖÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢ ÓĖĢÓĖ▒ÓĖ¦ÓĖŁÓĖóÓ╣łÓĖ▓ÓĖćÓĖüÓĖ▓ÓĖŻÓĖ¤ÓĖŁÓĖüÓ╣ĆÓĖćÓĖ┤Ó╣īÓ╣āÓ╣īÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒Ó╣īÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢ ŌĆó ÓĖŗÓĖĘÓ╣ēÓĖŁÓĖüÓĖŁÓĖćÓĖŚÓĖĖÓ╣īÓĖźÓĖćÓĖŚÓĖĖÓ╣īÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒Ó╣īÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓĖäÓĖŻÓĖ▒Ó╣ēÓĖćÓ╣ĆÓĖöÓĖĄÓĖóÓĖ¦(ÓĖĪÓĖĄÓĖäÓĖ¦ÓĖ▓ÓĖĪÓ╣ĆÓĖ¬ÓĖĄÓ╣łÓĖóÓĖćÓĖŚÓĖĄÓ╣łÓĖłÓĖ░ÓĖ¤ÓĖŁÓĖüÓ╣ĆÓĖćÓĖ┤Ó╣īÓĖĪÓĖ▓ÓĖüÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖöÓĖłÓĖ▓ÓĖüÓĖüÓĖ▓ÓĖŻÓ╣īÓĖ▓Ó╣ĆÓĖćÓĖ┤Ó╣īÓĖ¬ÓĖüÓĖøÓĖŻÓĖü ÓĖüÓ╣ēÓĖŁÓ╣īÓ╣āÓĖ½ÓĖŹÓ╣łÓĖĪÓĖ▓ÓĖźÓĖćÓĖŚÓĖĖÓ╣ī) ŌĆó ÓĖŗÓĖĘÓ╣ēÓĖŁÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒Ó╣īÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓĖŻÓĖ▓ÓĖóÓĖøÓĖĄÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓĖøÓĖ▒Ó╣īÓĖ£ÓĖź(Ó╣äÓĖöÓ╣ēÓĖŻÓĖ▒ÓĖÜÓ╣ĆÓĖćÓĖ┤Ó╣īÓĖ¬ÓĖ░ÓĖŁÓĖ▓ÓĖöÓ╣ĆÓĖøÓ╣ćÓ╣īÓĖćÓĖ¦ÓĖöÓ╣å) ŌĆó ÓĖŗÓĖĘÓ╣ēÓĖŁÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒Ó╣īÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓ╣üÓĖÜÓĖÜÓĖøÓĖŻÓĖ░ÓĖłÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓĖ¬ÓĖ╣ÓĖćÓĖ½ÓĖŻÓĖĘÓĖŁÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓĖøÓĖüÓĖĢÓĖ┤ÓĖ½ÓĖźÓĖ▓ÓĖóÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣ī(Ó╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓĖźÓĖöÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ¬Ó╣īÓ╣āÓĖł) ŌĆó ÓĖüÓĖ▓ÓĖŻÓ╣äÓĖ¢Ó╣łÓĖ¢ÓĖŁÓ╣īÓ╣ĆÓĖćÓĖ┤Ó╣īÓĖüÓ╣łÓĖŁÓ╣īÓĖäÓĖŻÓĖÜÓĖ¬ÓĖ▒ÓĖŹÓĖŹÓĖ▓Ó╣üÓĖĪÓ╣ēÓĖłÓĖ░Ó╣äÓĖöÓ╣ēÓ╣ĆÓĖćÓĖ┤Ó╣īÓĖäÓĖĘÓ╣īÓ╣īÓ╣ēÓĖŁÓĖóÓĖüÓĖ¦Ó╣łÓĖ▓Ó╣ĆÓĖöÓĖ┤ÓĖĪ ŌĆó ÓĖŗÓĖĘÓ╣ēÓĖŁÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓ╣īÓ╣ēÓĖŁÓĖóÓ╣āÓĖ½Ó╣ēÓĖ£Ó╣łÓĖ▓Ó╣īÓĖüÓ╣łÓĖŁÓ╣īÓ╣üÓĖźÓ╣ēÓĖ¦Ó╣ĆÓĖ×ÓĖ┤Ó╣łÓĖĪÓ╣ĆÓĖĢÓĖ┤ÓĖĪÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖó(Ó╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓ╣āÓĖ½Ó╣ēÓ╣äÓĖĪÓ╣łÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖĢÓĖŻÓĖ¦ÓĖłÓĖ¬ÓĖŁÓĖÜ) ŌĆó ÓĖüÓĖ╣Ó╣ēÓ╣ĆÓĖćÓĖ┤Ó╣īÓĖłÓĖ▓ÓĖüÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓ╣éÓĖöÓĖóÓ╣äÓĖĪÓ╣łÓĖ£Ó╣łÓĖŁÓ╣īÓĖłÓ╣łÓĖ▓ÓĖóÓĖäÓĖĘÓ╣ī(ÓĖøÓĖźÓ╣łÓĖŁÓĖóÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖ½ÓĖĪÓĖöÓĖŁÓĖ▓ÓĖóÓĖĖÓ╣äÓĖøÓ╣ĆÓĖŁÓĖć) ŌĆó Ó╣ĆÓĖøÓĖźÓĖĄÓ╣łÓĖóÓ╣īÓĖĪÓĖĘÓĖŁÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖéÓĖŁÓĖćÓ╣ĆÓĖłÓ╣ēÓĖ▓ÓĖéÓĖŁÓĖćÓĖ½ÓĖŻÓĖĘÓĖŁÓĖ£ÓĖ╣Ó╣ēÓĖŻÓĖ▒ÓĖÜÓĖ£ÓĖźÓĖøÓĖŻÓĖ░Ó╣éÓĖóÓĖŖÓ╣īÓ╣ī ŌĆó Ó╣āÓĖŖÓ╣ēÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓ╣ĆÓĖøÓ╣ćÓ╣īÓĖ½ÓĖźÓĖ▒ÓĖüÓĖŚÓĖŻÓĖ▒ÓĖ×ÓĖóÓ╣īÓ╣āÓ╣īÓĖüÓĖ▓ÓĖŻÓĖüÓĖ╣Ó╣ēÓ╣ĆÓĖćÓĖ┤Ó╣īÓĖłÓĖ▓ÓĖüÓĖśÓ╣īÓĖ▓ÓĖäÓĖ▓ÓĖŻ ÓĖŚÓĖĄÓ╣łÓĖĪÓĖ▓ : http://www.acamstoday.org/what-is-real-money-laundering-risk-in-life-insurance/
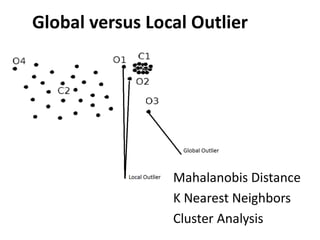
- 33. Global versus Local Outlier Mahalanobis Distance K Nearest Neighbors Cluster Analysis
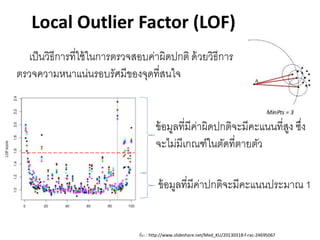
- 34. Local Outlier Factor (LOF) ÓĖŚÓĖĄÓ╣łÓĖĪÓĖ▓ : http://www.slideshare.net/Med_KU/20130318-f-rac-24695067 Ó╣ĆÓĖøÓ╣ćÓ╣īÓĖ¦ÓĖ┤ÓĖśÓĖĄÓĖüÓĖ▓ÓĖŻÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ēÓ╣āÓ╣īÓĖüÓĖ▓ÓĖŻÓĖĢÓĖŻÓĖ¦ÓĖłÓĖ¬ÓĖŁÓĖÜÓĖäÓ╣łÓĖ▓ÓĖ£ÓĖ┤ÓĖöÓĖøÓĖüÓĖĢÓĖ┤ÓĖöÓ╣ēÓĖ¦ÓĖóÓĖ¦ÓĖ┤ÓĖśÓĖĄÓĖüÓĖ▓ÓĖŻ ÓĖĢÓĖŻÓĖ¦ÓĖłÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ½Ó╣īÓĖ▓Ó╣üÓ╣īÓ╣łÓ╣īÓĖŻÓĖŁÓĖÜÓĖŻÓĖ▒ÓĖ©ÓĖĪÓĖĄÓĖéÓĖŁÓĖćÓĖłÓĖĖÓĖöÓĖŚÓĖĄÓ╣łÓĖ¬Ó╣īÓ╣āÓĖł ÓĖéÓ╣ēÓĖŁÓĖĪÓĖ╣ÓĖźÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖäÓ╣łÓĖ▓ÓĖ£ÓĖ┤ÓĖöÓĖøÓĖüÓĖĢÓĖ┤ÓĖłÓĖ░ÓĖĪÓĖĄÓĖäÓĖ░Ó╣üÓ╣īÓ╣īÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖ╣ÓĖć ÓĖŗÓĖČÓ╣łÓĖć ÓĖłÓĖ░Ó╣äÓĖĪÓ╣łÓĖĪÓĖĄÓ╣ĆÓĖüÓĖōÓĖæÓ╣īÓ╣āÓ╣īÓĖĢÓĖ▒ÓĖöÓĖŚÓĖĄÓ╣łÓĖĢÓĖ▓ÓĖóÓĖĢÓĖ▒ÓĖ¦ ÓĖéÓ╣ēÓĖŁÓĖĪÓĖ╣ÓĖźÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖäÓ╣łÓĖ▓ÓĖøÓĖüÓĖĢÓĖ┤ÓĖłÓĖ░ÓĖĪÓĖĄÓĖäÓĖ░Ó╣üÓ╣īÓ╣īÓĖøÓĖŻÓĖ░ÓĖĪÓĖ▓ÓĖō 1
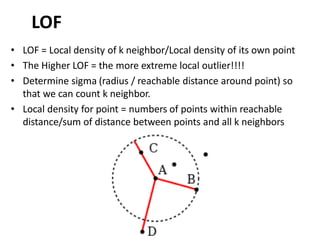
- 35. ŌĆó LOF = Local density of k neighbor/Local density of its own point ŌĆó The Higher LOF = the more extreme local outlier!!!! ŌĆó Determine sigma (radius / reachable distance around point) so that we can count k neighbor. ŌĆó Local density for point = numbers of points within reachable distance/sum of distance between points and all k neighbors LOF
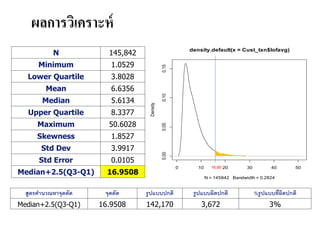
- 37. ÓĖ£ÓĖźÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣ī N 145,842 Minimum 1.0529 Lower Quartile 3.8028 Mean 6.6356 Median 5.6134 Upper Quartile 8.3377 Maximum 50.6028 Skewness 1.8527 Std Dev 3.9917 Std Error 0.0105 Median+2.5(Q3-Q1) 16.9508 ÓĖ¬ÓĖ╣ÓĖĢÓĖŻÓĖäÓĖ│ÓĖÖÓĖ¦ÓĖōÓĖ½ÓĖ│ÓĖłÓĖĖÓĖöÓĖĢÓĖ▒ÓĖö ÓĖłÓĖĖÓĖöÓĖĢÓĖ▒ÓĖö ÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜÓĖøÓĖüÓĖĢÓĖ┤ ÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜÓĖ£ÓĖ┤ÓĖöÓĖøÓĖüÓĖĢÓĖ┤ %ÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜÓĖŚÓĖĄÓ╣łÓĖ£ÓĖ┤ÓĖöÓĖøÓĖüÓĖĢÓĖ┤ Median+2.5(Q3-Q1) 16.9508 142,170 3,672 3% 0 10 20 30 40 50 0.000.050.100.15 density.default(x = Cust_txn$lofavg) N = 145842 Bandwidth = 0.2824 Density 16.95
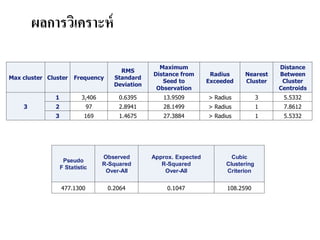
- 38. ÓĖ£ÓĖźÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣ī Max cluster Cluster Frequency RMS Standard Deviation Maximum Distance from Seed to Observation Radius Exceeded Nearest Cluster Distance Between Cluster Centroids 3 1 3,406 0.6395 13.9509 > Radius 3 5.5332 2 97 2.8941 28.1499 > Radius 1 7.8612 3 169 1.4675 27.3884 > Radius 1 5.5332 Pseudo F Statistic Observed R-Squared Over-All Approx. Expected R-Squared Over-All Cubic Clustering Criterion 477.1300 0.2064 0.1047 108.2590
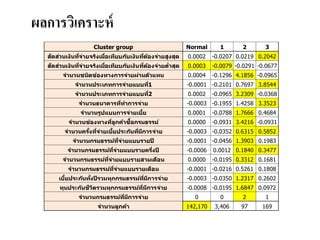
- 39. ÓĖ£ÓĖźÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣ī Cluster group Normal 1 2 3 ÓĖ¬ÓĖ▒ÓĖöÓĖ¬Ó╣łÓĖ¦ÓĖÖÓ╣ĆÓĖćÓĖ┤ÓĖÖÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓĖłÓĖŻÓĖ┤ÓĖćÓ╣ĆÓĖĪÓĖĘÓ╣łÓĖŁÓ╣ĆÓĖŚÓĖĄÓĖóÓĖÜÓĖü ÓĖ▒ÓĖÜÓ╣ĆÓĖćÓĖ┤ÓĖÖÓĖŚÓĖĄÓ╣łÓĖĢÓ╣ēÓĖŁÓĖćÓĖłÓ╣łÓĖ▓ÓĖóÓĖ¬ÓĖ╣ÓĖćÓĖ¬ÓĖĖÓĖö 0.0002 -0.0207 0.0219 0.2042 ÓĖ¬ÓĖ▒ÓĖöÓĖ¬Ó╣łÓĖ¦ÓĖÖÓ╣ĆÓĖćÓĖ┤ÓĖÖÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓĖłÓĖŻÓĖ┤ÓĖćÓ╣ĆÓĖĪÓĖĘÓ╣łÓĖŁÓ╣ĆÓĖŚÓĖĄÓĖóÓĖÜÓĖü ÓĖ▒ÓĖÜÓ╣ĆÓĖćÓĖ┤ÓĖÖÓĖŚÓĖĄÓ╣łÓĖĢÓ╣ēÓĖŁÓĖćÓĖłÓ╣łÓĖ▓ÓĖóÓĖĢÓ╣łÓĖ▓ÓĖ¬ÓĖĖÓĖö 0.0003 -0.0079 -0.0291 -0.0677 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŖÓĖÖÓĖ┤ÓĖöÓĖŖÓ╣łÓĖŁÓĖćÓĖŚÓĖ▓ÓĖćÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓĖ£Ó╣łÓĖ▓ÓĖÖÓĖĢÓĖ▒ÓĖ¦Ó╣üÓĖŚÓĖÖ 0.0004 -0.1296 4.1856 -0.0965 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖøÓĖŻÓĖ░Ó╣ĆÓĖĀÓĖŚÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓĖŚÓĖĄÓ╣ł1 -0.0001 -0.2101 0.7697 3.8544 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖøÓĖŻÓĖ░Ó╣ĆÓĖĀÓĖŚÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓĖŚÓĖĄÓ╣ł2 0.0002 -0.0965 3.2309 -0.0368 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖśÓĖÖÓĖ▓ÓĖäÓĖ▓ÓĖŻÓĖŚÓĖĄÓ╣łÓĖŚÓĖ▓ÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖó -0.0003 -0.1955 1.4258 3.3523 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖó 0.0001 -0.0788 1.7666 0.4684 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŖÓ╣łÓĖŁÓĖćÓĖŚÓĖ▓ÓĖćÓĖŚÓĖĄÓ╣łÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓ÓĖŗÓĖĘÓ╣ēÓĖŁÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣ī 0.0000 -0.0931 3.4216 -0.0931 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖäÓĖŻÓĖ▒Ó╣ēÓĖćÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓĖøÓĖŻÓĖ░ÓĖü ÓĖ▒ÓĖÖÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖó -0.0003 -0.0352 0.6315 0.5852 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓĖŻÓĖ▓ÓĖóÓĖøÓĖĄ -0.0001 -0.0456 1.3903 0.1983 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓĖŻÓĖ▓ÓĖóÓĖäÓĖŻÓĖČÓ╣łÓĖćÓĖøÓĖĄ -0.0006 0.0012 0.1840 0.3477 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓĖŻÓĖ▓ÓĖóÓĖ¬ÓĖ▓ÓĖĪÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖ 0.0000 -0.0195 0.3312 0.1681 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓĖŻÓĖ▓ÓĖóÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖ -0.0001 -0.0216 0.5261 0.1808 Ó╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓĖøÓĖŻÓĖ░ÓĖü ÓĖ▒ÓĖÖÓĖŚ ÓĖ▒Ó╣ēÓĖćÓĖøÓĖĄ ÓĖŻÓĖ¦ÓĖĪÓĖŚÓĖĖÓĖüÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖó -0.0003 -0.0350 1.2317 0.2602 ÓĖŚÓĖĖÓĖÖÓĖøÓĖŻÓĖ░ÓĖü ÓĖ▒ÓĖÖÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓĖŻÓĖ¦ÓĖĪÓĖŚÓĖĖÓĖüÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖó -0.0008 -0.0195 1.6847 0.0972 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖó 0 0 2 1 ÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓ 142,170 3,406 97 169
- 40. ŌĆó Normal ÓĖüÓĖźÓĖĖÓ╣łÓĖĪÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓ╣ĆÓĖēÓĖźÓĖĄÓ╣łÓĖóÓ╣ĆÓĖ×ÓĖĄÓĖóÓĖć 1 ÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣ī ÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓ÓĖĪÓĖĄÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖŚÓĖĖÓĖüÓĖŖÓĖÖÓĖ┤ÓĖö (ÓĖŻÓĖ▓ÓĖóÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖ,ÓĖŻÓĖ▓ÓĖó ÓĖ¬ÓĖ▓ÓĖĪÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖ,ÓĖŻÓĖ▓ÓĖóÓĖ½ÓĖüÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖÓ╣üÓĖźÓĖ░ÓĖŻÓĖ▓ÓĖóÓĖøÓĖĄ) Ó╣üÓĖźÓĖ░Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓ╣ĆÓĖĢÓ╣ćÓĖĪÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖöÓ╣ēÓĖ¦ÓĖóÓĖŖÓ╣łÓĖŁÓĖćÓĖŚÓĖ▓ÓĖćÓ╣ĆÓĖöÓĖĄÓĖóÓĖ¦ ŌĆó Cluster 1 ÓĖĪÓĖĄÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜÓ╣ĆÓĖöÓĖĄÓĖóÓĖ¦ÓĖüÓĖ▒ÓĖÜÓĖüÓĖźÓĖĖÓ╣łÓĖĪ Normal ŌĆó Cluster 2 ÓĖüÓĖźÓĖĖÓ╣łÓĖĪÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓ╣ĆÓĖēÓĖźÓĖĄÓ╣łÓĖóÓĖĪÓĖ▓ÓĖüÓĖüÓĖ¦Ó╣łÓĖ▓ 2 ÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣ī ÓĖŗÓĖČÓ╣łÓĖćÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓Ó╣ĆÓĖÖÓ╣ēÓĖÖÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓ╣üÓĖÜÓĖÜÓĖŻÓĖ▓ÓĖó Ó╣ĆÓĖöÓĖĘÓĖŁÓĖÖÓ╣üÓĖźÓĖ░ÓĖŻÓĖ▓ÓĖóÓĖøÓĖĄÓ╣éÓĖöÓĖóÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓ╣ĆÓĖĢÓ╣ćÓĖĪÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓ╣āÓĖÖÓĖ½ÓĖźÓĖ▓ÓĖóÓ╣å ÓĖŖÓ╣łÓĖŁÓĖćÓĖŚÓĖ▓ÓĖćÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓĖüÓĖ▒ÓĖÜÓĖĢÓĖ▒ÓĖ¦Ó╣üÓĖŚÓĖÖÓĖéÓĖ▓ÓĖóÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖ ŌĆó Cluster 3 ÓĖźÓĖ╣ÓĖüÓĖäÓ╣ēÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖŖÓĖĄÓĖ¦ÓĖ┤ÓĖĢÓ╣ĆÓĖēÓĖźÓĖĄÓ╣łÓĖóÓĖĪÓĖ▓ÓĖüÓĖüÓĖ¦Ó╣łÓĖ▓ 1 ÓĖüÓĖŻÓĖĪÓĖśÓĖŻÓĖŻÓĖĪÓ╣īÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖüÓĖźÓĖĖÓ╣łÓĖĪÓĖŚÓĖĄÓ╣łÓ╣ĆÓĖÖÓ╣ēÓĖÖÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣ĆÓĖÜÓĖĄÓ╣ēÓĖóÓ╣üÓĖÜÓĖÜÓĖŻÓĖ▓ÓĖó ÓĖ¬ÓĖ▓ÓĖĪÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖÓ╣üÓĖźÓĖ░ÓĖŻÓĖ▓ÓĖóÓĖ½ÓĖüÓ╣ĆÓĖöÓĖĘÓĖŁÓĖÖÓ╣üÓĖźÓĖ░Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖüÓĖ▓ÓĖŻÓĖłÓ╣łÓĖ▓ÓĖóÓ╣üÓĖÜÓĖÜÓ╣ĆÓĖüÓĖ┤ÓĖÖÓĖłÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓ╣āÓĖÖÓĖ½ÓĖźÓĖ▓ÓĖóÓ╣å ÓĖŖÓ╣łÓĖŁÓĖćÓĖŚÓĖ▓ÓĖćÓĖüÓĖ▓ÓĖŻÓĖŖÓĖ▓ÓĖŻÓĖ░Ó╣ĆÓĖćÓĖ┤ÓĖÖ Ó╣ĆÓĖŖÓ╣łÓĖÖ Ó╣ĆÓĖćÓĖ┤ÓĖÖÓĖ¬ÓĖöÓĖ½ÓĖŻÓĖĘÓĖŁÓĖÜÓĖ▒ÓĖĢÓĖŻ Ó╣ĆÓĖäÓĖŻÓĖöÓĖ┤ÓĖĢ ÓĖ¬ÓĖŻÓĖĖÓĖøÓĖ£ÓĖĪÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣ī