Statistika
Download as ppt, pdf3 likes33,354 views
Dokumen ini menjelaskan metode perhitungan statistik data berkelompok, termasuk rataan hitung, median, dan modus, serta cara menghitung kuartil, desil, dan persentil. Terdapat contoh perhitungan yang menunjukkan penggunaan rumus-rumus untuk menentukan nilai statistik tersebut dari tabel distribusi frekuensi. Selain itu, juga dibahas mengenai simpangan rata-rata, variansi, dan simpangan baku pada data berkelompok.
Statistika
- 1. STATISTIK DATA BERKELOMPOK Mean (Rataan Hitung) (ii). Metode Titik Tengah ¡Æfx X= ¡Æf i i i (ii). Metode Rataan Sementara X = Xs ¡Æfd + ¡Æf i i i (iii). Metode Pengkodean(Coding) Xs = nilai rata-rata hitung sementara di = Xi ¨C Xs Xi = titik tengah kelas c = panjang kelas ? ¡Æ f iU i ? ?c X = Xs +? ? ¡Æf ? i ? ? xi ? xs Ui = c
- 2. tb = Tepi bawah kelas median Median ? n?¡Æ M e = tb + ? ? f0 ? 1 2 f ? ?c ? ? c = panjang kelas ¡Æf = jumlah frekuensi sebelum median f0 = frekuensi median n = jumlah semua frekuensi Modus Modus untuk data berkelompok ditentukan dengan rumus : ? d1 ? M 0 = tb + ? ? d + d ?C ? 2 ? ? 1 tb = tepi bawah kelas c = panjang kelas fo = frekuensi kelas modus d1 = f0 ¨C f -1 d2 = f0 ¨C f+1 f+1 = frekuensi kelas sesudah kelas modus f-1 = frekuensi kelas sebelum kelas modus
- 3. Contoh : Perhatikan Tabel Distribusi frekuensi disamping Tentukanlah : a. Rataan Hitung (Mean) b. Median c. Modus Jawab : Cara 1 : Interval fi xi fixi 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 24 29 34 39 120 348 306 156 30 930 Interval Frekuensi 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 ¡Æfx X= ¡Æf i i i 930 = 30 = 31
- 4. Jawab : Cara 2 : Interval fi xi di = x i ¨C xs fidi 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 24 29 34 39 -5 0 5 10 -25 0 45 40 30 X s = 29 X = Xs ¡Æfd + ¡Æf i i 60 = 29 + 30 = 29 + 2 60 = 31 Cara 3 : Interval fi xi ui fiui 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 24 29 34 39 -1 0 1 2 -5 0 9 8 30 12 X s = 29 Ui = xi ? xs c ? ¡Æ f iU i ? ?c X = Xs +? ? ¡Æf ? i ? ? 12 .5 30 = 29 + 2 = 31 = 29 + i
- 5. Jawab : Median Interval fi ¡Æfk 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 5 17 26 30 ? 1 n?¡Æ M e = tb + ? 2 ? f0 ? ? 10 ? = 26,5 + ? ?5 ? 12 ? = 26,5 + 4,17 = 30,67 Modus Interval fi 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 d1 = 12 ¨C 5 = 7 d2 = 12 ¨C 9 = 3 f ? ? 1 (30) ? 5 ? ?c = 26,5 + ? 2 ?5 ? ? 12 ? ? ? d1 ? M 0 = tb + ? ? d + d ?C ? 2 ? ? 1 ? 7 ? = 26,5 + ? ?5 ? 7 +3? = 26,5 + 3,5 = 30
- 6. Kuartil Kuartil untuk data berkelompok dapat ditentukan dengan menggunakan rumus :tb = Tepi bawah kelas kuartil ke i (1,2,3) i ? 4 n ? ¡Æ f k ? c = panjang kelas ?c Qi = tb + ? ? ? ¡Æf = jumlah frekuensi sebelum kuartil ke-i f0 ? ? f0 = frekuensi kuartil ke-i Desil i ? 10 n ? ¡Æ f k ? ?c Di = tb + ? ? ? f0 ? ? Persentil i ? 100 n ? ¡Æ f k ? ?c Pi = tb + ? ? ? f0 ? ? n = jumlah semua frekuensi tb = Tepi bawah kelas desil ke-i (1,2,3....9) tb = Tepi bawah kelas persentil ke-i (1,2,3....99)
- 7. Contoh : Interval b. Jangkauan Antar Kuartil c. Simpangan Kuartil Jawab : Interval fi ¡Æfk 1¨C5 6 ¨C 10 11 ¨C 15 16 ¨C 20 21 ¨C 25 26 ¨C 30 3 5 10 15 4 3 3 8 18 33 37 40 Letak Q1 pada frekuensi = ?(40)= 10 di kelas 11 ¨C 15 Frekuensi 1¨C5 6 ¨C 10 11 ¨C 15 16 ¨C 20 21 ¨C 25 26 ¨C 30 Perhatikan Tabel Distribusi frekuensi disamping Tentukanlah : a. Q1, Q2 dan Q3 3 5 10 15 4 3 ? 1 n ? ¡Æ fk ? ?c Q1 = tb + ? 4 ? ? f0 ? ? ? 1 (40) ? 8 ? = 10,5 + ? 4 ?5 ? 10 ? ?2? = 10,5 + ? ? ?2? = 10,5 + 1 = 11,5
- 8. Interval fi ¡Æfk 1¨C5 6 ¨C 10 11 ¨C 15 16 ¨C 20 21 ¨C 25 26 ¨C 30 3 5 10 15 4 3 3 8 18 33 37 40 Letak Q2 pada frekuensi = ? (40)= 20 di kelas 16 ¨C 20 Interval fi ¡Æfk 1¨C5 6 ¨C 10 11 ¨C 15 16 ¨C 20 21 ¨C 25 26 ¨C 30 3 5 10 15 4 3 3 8 18 33 37 40 Letak Q3 pada frekuensi = ?(40)= 30 di kelas 16 ¨C 20 ? 1 n ? ¡Æ fk ? ?c Q2 = tb + ? 2 ? ? f0 ? ? ? 1 (40) ? 18 ? = 15,5 + ? 2 ?5 15 ? ? ?2? = 15,5 + ? ? ?3? = 15,5 + 0,67 = 16,17 ? 3 n ? ¡Æ fk ? ?c Q3 = tb + ? 4 ? ? f0 ? ? ? 3 (40) ? 18 ? = 15,5 + ? 4 ?5 15 ? ? ? 12 ? = 15,5 + ? ? ?3? = 15,5 + 4 = 19,5
- 9. b Jangkauan Antar Kuartil = Q3 ¨C Q1 = 19,5 ¨C 11,5 =8 c. Jangkauan Antar Kuartil = ?(Q3 ¨C Q1) = ?(19,5 ¨C 11,5) = ? (8) =4 Contoh : Perhatikan Tabel Distribusi frekuensi disamping Tentukanlah : a. Desil ke-3 b. Persentil ke 85 Interval Frekuensi 4¨C7 8 ¨C 11 12 ¨C 15 16 ¨C 19 20 ¨C 23 24 ¨C 27 8 10 16 40 16 10
- 10. Jawab : Interval fi ¡Æfk 4¨C7 8 ¨C 11 12 ¨C 15 16 ¨C 19 20 ¨C 23 24 ¨C 27 8 10 16 40 16 10 8 18 34 74 90 100 Letak Q2 pada frekuensi 3 = 10 (100)= 30 di kelas 12 ¨C 15 Interval fi ¡Æfk 4¨C7 8 ¨C 11 12 ¨C 15 16 ¨C 19 20 ¨C 23 24 ¨C 27 8 10 16 40 16 10 8 18 34 74 90 100 Letak Q2 pada frekuensi 85 = 100 (100)= 85 di kelas 20 ¨C 23 3 ? 10 n ? ¡Æ f k ? ?c D3 = tb + ? ? ? f0 ? ? 3 ? 10 (100) ? 18 ? = 11,5 + ? ?4 16 ? ? ? 12 ? = 11,5 + ? ? ?4? = 11,5 + 3 = 14,5 85 ? 100 n ? ¡Æ f k ? ?c P85 = tb + ? ? ? f0 ? ? 85 ? 100 (100) ? 74 ? = 19,5 + ? ?4 16 ? ? ? 11 ? = 19,5 + ? ? ?4? = 19,5 + 2,75 = 22,25
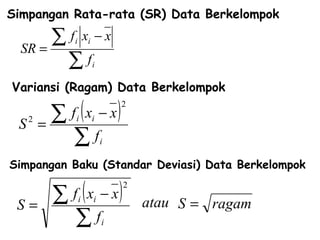
- 11. Simpangan Rata-rata (SR) Data Berkelompok ¡Æ f x ?x SR = ¡Æf i i i Variansi (Ragam) Data Berkelompok S 2 ¡Æ f ( x ? x) = ¡Æf i 2 i i Simpangan Baku (Standar Deviasi) Data Berkelompok S= ¡Æ f ( x ? x) ¡Æf i i i 2 atau S = ragam
- 12. Contoh : Interval Perhatikan Tabel Distribusi frekuensi disampingTentukanlah 22 ¨C 26 27 ¨C 31 : 32 ¨C 36 a. Simpangan Rata-rata 37 ¨C 41 b. Ragam (variansi) c. Simpangan Baku Jawab : a. Simpangan rata-rata Interval fi xi fixi |xi ¨C x| fi |xi ¨C x| 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 24 29 34 39 120 348 306 156 7 2 3 8 35 24 27 32 30 930 108 Frekuensi 5 12 9 4 ¡Æfx X= ¡Æf i i = i 930 = 31 30 ¡Æ f x ?x SR = ¡Æf i i i 108 = 30 = 3,6
- 13. Jawab : b. ragam (variansi) Interval fi xi f ix i (xi ¨C x) (xi ¨C x) 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 5 12 9 4 24 29 34 39 120 348 306 156 -7 -2 3 8 49 4 9 64 30 2 fi (xi ¨C x) 2 2 2 22 ¨C 26 27 ¨C 31 32 ¨C 36 37 ¨C 41 fi 5 12 9 4 30 xi 24 29 34 39 fixi 120 348 306 156 930 (xi ¨C x) -7 -2 3 8 (xi ¨C x) 49 4 9 64 fi (xi ¨C x) 245 48 81 256 630 i 630 = 30 = 21 c. Simpangan Baku (standar deviasi) Interval i i 630 2 i i i 245 48 81 256 930 ¡Æ f x = 930 = 31 X= 30 ¡Æf ¡Æ f ( x ? x) S = ¡Æf 2 ¡Æ f x = 930 = 31 X= 30 ¡Æf ¡Æ f ( x ? x) S= ¡Æf i i i 2 i i i 630 = = 21 30
- 14. 37. Persentil ke-75 dari data: 8, 6, 4, 3, 2, 9, 10, 15, 12, 14 adalah ¡. a. 11 b. 11,5 c. 12,5 d. 12,75 e. 13 38. Simpangan rataan hitung data 10, 10, 9,8, 8, 7, 7, 6, 6, 5 adalah .... a. 7,6 b. 6,6 c. 2,8 d. 2,2 e. 1,4
- 15. 39. Simpangan baku dari tabel di bawah ini adalah ¡. Interval Frekuensi a. 6 3 b. 7 2 41 ¨C 50 1 51 ¨C 60 7 c. 4 6 61 ¨C 70 10 d. 91 71 ¨C 80 6 e. 86 81 ¨C 90 2 40. Nilai 4 5 6 8 10 Frekuensi 20 40 70 a 10 Dalam tabel di atas, nilai rataan hitung ujian matematika adalah 6. Oleh karena itu, a adalah .... a.0 b.5 c.10 d.20 e. 30
- 16. Persentil (data tunggal) Jika data dibagi menjadi 100 bagian yang sama, maka ukuran itu disebut persentil. Letak persentil dirumuskan dengan: Keterangan: Pi = persentil ke-i i = 1, 2, 3, . . ., 99 n = banyaknya data Contoh : Diketahui: 9, 10, 11, 6, 8, 7, 7, 5, 4, 5, tentukan persentil ke-30 dan persentil ke-75. Jawab : Data diurutkan: 4, 5, 5, 6, 7, 7, 8, 9, 10, 11
- 17. Jawab :