Steiner Minimal Trees
- 1. Steiner Tree Applications Presented by T. N. Badri
- 2. The Steiner problem dates back to Pierre Fermat. Even Napolean has worked on this problem. Consider three points V 1 , V 2 , and V 3 . The shortest network interconnecting these three points is the sum of the two shortest sides of the triangle. If one includes a fourth point S 1 in the plane of the triangle, one can find a much shorter interconnecting network. V 1 V 2 V 3 V 1 V 2 V 3 S 1
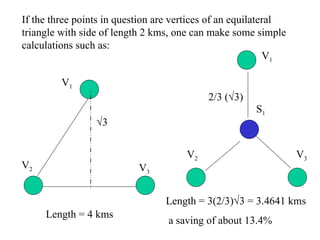
- 3. If the three points in question are vertices of an equilateral triangle with side of length 2 kms, one can make some simple calculations such as: Length = 4 kms 2/3 ( ï 3) Length = 3(2/3) ï 3 = 3.4641 kms a saving of about 13.4% ï 3 V 1 V 2 V 3 V 1 V 2 V 3 S 1
- 4. If it costs about Rs. 3 lakhs to lay one km of road this is a saving of 0.134 * 300,000 * 4 = Rs. 160,800 on an initial total cost of Rs. 12 lakhs.
- 5. Steiner points have some properties Exactly three edges meet at every Steiner vertex. The angles between the edges meeting at a Steiner vertex is 120 degrees. If there are N vertices then we can use a maximum of N-2 Steiner vertices.
- 6. MST length = 1 + ï ï 3 SMT length is 2.6458 A saving of 3.1588% 1 ï 3 2 (-0.2857, 0.2474)
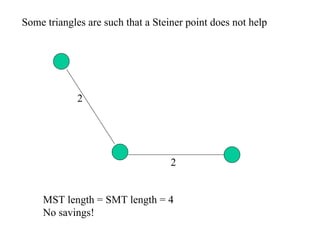
- 7. Some triangles are such that a Steiner point does not help 2 2 MST length = SMT length = 4 No savings!
- 8. Geometric Construction using compass and straight edge
- 9. Four terminal sites in 3d with one Steiner point Four terminal sites in 3d with two Steiner points
- 10. Steiner trees with the rectilinear metric appear when laying down conductive pathways on a printed circuit board.
- 11. HANAN GRID
- 12. Development of Path Topology in 2d (Counter-clockwise from top right)
- 13. Planar-Sausage with 8 terminal sites Conjectured infinite 2d structure with best Steiner Ratio ï 3/2
- 14. Planar-Sausage with 9 terminal sites Conjectured infinite 2d structure with best Steiner Ratio ï 3/2
- 15. Planar-Sausage with 10 terminal sites Conjectured 2d structure with best Steiner Ratio ï 3/2
- 16. Planar-Sausage with 11 terminal sites Conjectured infinite 2d structure with best Steiner Ratio = ï 3/2
- 17. Steiner Ratio in 2d falls to ï 3/2 as the number of terminal sites increase
- 18. R-Sausage Minimum Spanning Tree
- 19. R-Sausage Conjectured infinite 3d structure with best Steiner Ratio
- 20. Another view of 3d sausage Minimum Spanning Tree Steiner Minimal Tree
- 21. Steiner Ratio in 3d falls to ïŧ 0.784 as the number of terminal sites increase
- 22. Four types of Steiner points - according to neighbouring vertices
- 23. R-Sausage structure is preserved under composition. It is a semi-group.
- 24. Topology for Even and Odd Sized R-Sausages in 3d
- 25. d1 d2 d3 (x2,y2) (x1, y1) (x3,y3) (x,y) The average of the vertex coordinates weighted by their reciprocal distances from the Steiner point.
- 26. Depth First Search of point set Heuristic for large point set
- 27. Depth First Search of point set â The first Steiner point Heuristic for large point set
- 28. Depth First Search of point set â The second Steiner point Heuristic for large point set
- 29. Depth First Search of point set â The third Steiner point Heuristic for large point set
- 30. Depth First Search of point set â The fourth Steiner point Heuristic for large point set
- 31. Depth First Search of point set â Return to root node Heuristic for large point set
- 32. Depth First Search of point set â First Steiner vertex Heuristic for large point set
- 33. Depth First Search of point set â Second Steiner vertex Heuristic for large point set
- 34. Depth First Search of point set â Third Steiner vertex Heuristic for large point set
- 35. Depth First Search of point set â Fourth Steiner vertex Heuristic for large point set
- 36. Depth First Search of point set â Fifth Steiner vertex Heuristic for large point set
- 37. Steiner Tree and Minimum Spanning Tree for a small random point set in unit cube Minimal Interconnecting Tree for data without any structure
- 38. Steiner Tree and Minimum Spanning Tree for a medium sized random point set in unit cube Minimal Interconnecting Tree for data without any structure
- 39. Steiner Tree and Minimum Spanning Tree for Hundred random points in unit cube Minimal Interconnecting Tree for data without any structure
- 40. Steiner Tree and Minimum Spanning Tree for 500 random points in unit cube Minimal Interconnecting Tree for data without any structure
- 41. Amino Acid Sequence of a Protein (Lysozyme)
- 42. Network of Amide Planes in a Protein
- 43. Three Dimensional Structure of Two Amide Planes
- 44. THANK YOU