Struktur data 05 (bs avl tree)
- 1. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah BAGIAN VBAGIAN V
- 2. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree Binary Search Tree adalah Binary Tree dengan ketentuan sebagai berikut: 1. Semua Left child harus lebih kecil dari Parent dan Right child. 2. Semua Right child harus lebih besar dari Parent dan Left child. 3. Parent harus lebih besar dari Left Subtree dan harus lebih kecil dari Right Subtree. 4. Tidak boleh ada node yang mempunyai nilai yang sama, dengan kata lain tidak boleh terjadi duplikasi data.
- 3. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree Target node Karena ketentuan diatas, maka Binary Search tree dapat digunakan untuk tempat penyimpa-nan data secara terurut, sehingga pencarian data (searching) bisa lebih efisien. Untuk itu dapat ditentukan suatu target node yaitu suatu node yang berisi data yang akan dicari.
- 4. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree Gufron Edi Kemal Halim SylviaCecilia Farid
- 5. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree Operasi-operasi pada Binary Search tree. Semua operasi pada Binary tree dapat digunakan pada Binary Search tree, kecuali: Insert Update Deletsub Perlu perubahan pada operasi Insert dan Delete sehingga urutan data didalam tree dapat dipertahankan.
- 6. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree Insert(elemen_type e) ŌĆó Insert selalu dimulai dari Root node. ŌĆó Bila tree kosong, maka node baru sebagai Root node. ŌĆó Bila tidak kosong nilai e dibandingkan dengan nilai Root. ŌĆó Bila lebih kecil insert ke subtree kiri. ŌĆó Bila lebih besar insert ke subtree kanan. Contoh, Insert: 45, 23, 12, 78, 63, 96, 27
- 7. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree 33 21 50 14 25 10 18 40 62 2. Delete( ) 29 43 57 26
- 8. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah Binary Search TreeBinary Search Tree Tiga keadaan delete:Tiga keadaan delete: 1.1. Delete node leafDelete node leaf o Contoh: Delete(26), tidak ada pengganti.Contoh: Delete(26), tidak ada pengganti. 2.2. Delete node selain leaf, anak 1Delete node selain leaf, anak 1 o Contoh: Delete(62), pengganti adalah anakContoh: Delete(62), pengganti adalah anak satu-satunya.satu-satunya. 3.3. Delete node selain leaf, anak 2Delete node selain leaf, anak 2 o Contoh: Delete(33), pengganti adalah salah satuContoh: Delete(33), pengganti adalah salah satu dari dua anak, predecessor atau successor.dari dua anak, predecessor atau successor.
- 9. Binary Search TreeBinary Search Tree ’ü« Predecessor(33) = 29Predecessor(33) = 29 ’ü« Successor(33) = 40Successor(33) = 40 Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah 33 21 50 14 25 10 18 40 62 29 43 57 26
- 10. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree ’ü« Kelemahan yang dialami olehKelemahan yang dialami oleh Binary Search TreeBinary Search Tree adalahadalah kemungkinan bentuk tree yang didapat adalah bentukkemungkinan bentuk tree yang didapat adalah bentuk SkewedSkewed (Binary tree miring) sehingga pencarian menjadi(Binary tree miring) sehingga pencarian menjadi sekuensial.sekuensial. ’ü« Untuk menghindari hal tersebut, digunakan AVL tree,Untuk menghindari hal tersebut, digunakan AVL tree, dengan sifat sebagai berikut:dengan sifat sebagai berikut: PerbedaanPerbedaan ketinggianketinggian antara subtree kiri dengan subtreeantara subtree kiri dengan subtree kanan tidak lebih dari 1.kanan tidak lebih dari 1. AVL-Tree adalah Binary Search Tree yang menjagaAVL-Tree adalah Binary Search Tree yang menjaga ketinggian subtree kiri dengan subtree kananketinggian subtree kiri dengan subtree kanan tidak lebih dari 1.tidak lebih dari 1.
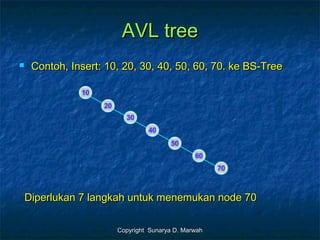
- 11. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree ’ü« Contoh, Insert: 10, 20, 30, 40, 50, 60, 70. ke BS-TreeContoh, Insert: 10, 20, 30, 40, 50, 60, 70. ke BS-Tree 20 10 70 50 40 30 60 Diperlukan 7 langkah untuk menemukan node 70Diperlukan 7 langkah untuk menemukan node 70
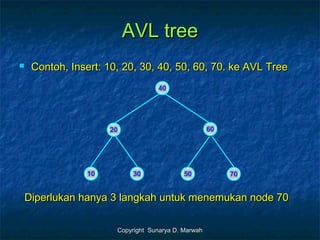
- 12. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 40 20 60 10 30 50 70 ’ü« Contoh, Insert: 10, 20, 30, 40, 50, 60, 70. ke AVL TreeContoh, Insert: 10, 20, 30, 40, 50, 60, 70. ke AVL Tree Diperlukan hanya 3 langkah untuk menemukan node 70Diperlukan hanya 3 langkah untuk menemukan node 70
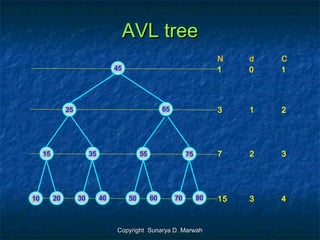
- 13. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 45 25 65 15 35 55 75 10 20 30 40 50 60 70 80 N d C 1 0 1 3 1 2 7 2 3 15 3 4
- 14. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree ’ü« Secara umum dapat dituliskan hubungan jumlah nodeSecara umum dapat dituliskan hubungan jumlah node (N) dengan pathlength (d) adalah:(N) dengan pathlength (d) adalah: N = 2N = 2(d+1)(d+1) ŌĆō 1ŌĆō 1 22(d+1)(d+1) == N + 1N + 1 loglog2222(d+1)(d+1) == loglog22 (N + 1)(N + 1) d + 1 = logd + 1 = log22 (N + 1)(N + 1) Karena jumlah langkah (C) = d + 1, makaKarena jumlah langkah (C) = d + 1, maka C = logC = log22 (N + 1)(N + 1)
- 15. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 20 10 50 5 12 4 6 40 65 AVL-Tree ?
- 16. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 20 10 50 5 12 4 6 40 AVL-Tree ?
- 17. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 20 10 50 5 12 6 40 AVL-Tree ?
- 18. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 20 10 50 5 6 40 AVL-Tree ?
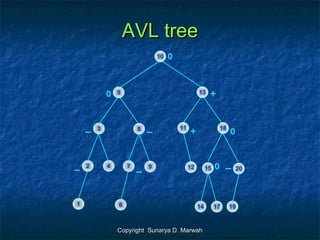
- 19. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree Keseimbangan subtree kiri dan kanan, dijaga dengan suatu mekanisme rotasi, untuk itu perlu diterapkan beberapa ketentuan sebagai berikut: 1.Tanda keseimbangan subtree: a. Node parent diberi tanda 0, bila ketinggian subtree kiri = subtree kanan b. Node parent diberi tanda +, bila ketinggian subtree kiri < subtree kanan c. Node parent diberi tanda -, bila ketinggian subtree kiri > subtree kanan
- 20. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 20 10 50 5 12 40 65 Search path untuk data 17 2. Search Path Path dimana node baru akan melaluinya untuk sampai pada posisi insert. Contoh: Insert(17)
- 21. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 3. Pivot node Pivot node adalah node yang: a. berada di Search-path b. bertanda + atau ŌĆō c. paling dekat dengan node baru PIVOT Pivot node merupakan sumbu putar, bila regenerasi tree diperlukanPivot node merupakan sumbu putar, bila regenerasi tree diperlukan
- 22. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 20 10 50 5 16 4 6 40 65 30 4614 61 76 54 63
- 23. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree Operasi Insert Kasus 1 Tidak terdapat pivot node, maka node baru langsung masuk tanpa harus melihat keseimbangan subtree. Kasus 2 Terdapat pivot node, periksa keseimbangan subtree, bila node baru tidak menyebabkan perbedaan ketinggian subtree > 1 maka node dapat masuk tanpa regenerasi tree. Keseimbangan subtree dilihat dari pivot node.Keseimbangan subtree dilihat dari pivot node.
- 24. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree Kasus 3 Terdapat pivot node, periksa keseimbangan subtree, bila node baru menyebabkan perbedaan ketinggian subtree > 1 maka node masuk dengan melakukan regenerasi tree. ’ü« Insert: 40, 60, 20, 30, 50, 10, 70.Insert: 40, 60, 20, 30, 50, 10, 70. ’ü« Insert: 30, 20, 10, 60, 50, 70, 40.Insert: 30, 20, 10, 60, 50, 70, 40. ’ü« Insert: 50, 60, 70, 30, 20, 10, 40.Insert: 50, 60, 70, 30, 20, 10, 40.
- 25. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree Operasi Delete Pada operasi delete, tidak ada pivot node, karena tidak ada node baru yang akan masuk. Sebagai acuan bila operasi delete menyebabkan tree harus regenerasi, dilaku- kan pemeriksaan secara berjenjang mulai dari anak nodedari anak node yang dihapusyang dihapus dimana node pengganti berada, dilanjutkan ke posisi node yang dihapus, kemudian terus naik hingga Root node. Selama pemeriksaan dapat terjadi beberapa rotasi baik rotasi tunggal maupun rotasi ganda, dengan demikian operasi delete merupakan operasi yang sangat kompleks, lebih sulit dari operasi insert.
- 26. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 13 5 16 3 2 4 14 18 8 11 17 2015 1 7 9 12 19 6 Delete node 16 10
- 27. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree Menurut aturan Binary Search tree, pengganti node 16 dapat diambil dari subtree kiri (node 15) atau dari subtree kanan (node 17). Dalam contoh ini, pengganti diambil dari subtree kiri. Pemeriksaan: 1. Node 14, sebagai anak kiri node 15 adalah leaf node (bertanda 0, meskipun tidak ditulis). 2. Node 15, sebagi pengganti node 16 yang dihapus, memiliki subtree kiri dan subtree kanan dengan selisih ketinggian > 1, sehingga harus dilakukan regenerasi. Karena node 15 mempunyai tanda + sama dengan tanda node 18, maka dilakukan rotasi kiri tunggal.
- 28. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree Pemeriksaan (lanjutan): 3. Setelah rotasi selesai, node 18 menggantikan node 15. 4. Node 13 sebagai parent dari node 18, memiliki subtree kiri dan subtree kanan dengan selisih > 1, sehingga harus dilakukan regenerasi. Karena node 13 adalah mempunyai tanda ŌĆō sedangkan anak sebelah kiri, yaitu node 5 mempunyai tanda +, oleh karena itu harus dilakukan rotasi ganda. 5. Node 13 adalah Root node, dengan demikian bila rotasi telah dilaksanakan, maka seluruh proses pemeriksaan selesai, dan hasilnya akan berupa AVL tree.
- 29. Copyright Sunarya D. MarwahCopyright Sunarya D. Marwah AVL treeAVL tree 10 5 3 2 4 7 9 15 13 1 6 8 11 18 12 20 14 17 19