�ݺ�ߣ

ASSIGNMENT PRESENTATION 1
STACK APPLICATION -
PARENTHESES MATCHING
TEAM – 3
• Amirthavarshyny.K (13MX02)
• Darsini.R (13MX07)
• Deepa.M (13MX08)
• Hemashri.AVM (13MX15)
• Kalaivani.M (13MX18)
• Sindhu Bharathi.A (13MX44)

SYNOPSIS :
 Introduction
 Operations in stack
 Stack Overflow & Underflow
 PUSH Algorithm
 POP Algorithm
 Applications of Stack
 Parentheses Checking or Matching
 References

STACK :
 It is an Abstract Data Type (ADT).
 It is a linear data structure.
 Follows LIFO (Last In First Out) data structure.
 Only two operations are supported.
 Real time examples:
 a stack of plates, a stack of coins, batteries in
flashlight…

OPERATIONS:
 PUSH:
- It is to insert an element into the
stack.
 POP:
- It is to remove the element from the
stack.

STACK OVERFLOW :
If we insert an element into stack which is
FULL, the stack is OVERFLOW.
STACK UNDERFLOW :
If we delete an element from stack which is
EMPTY, the stack is UNDERFLOW.

PUSH ALGORTHIM:
push(array,n,top,item)
{
if(top=n)
then stack full
else
top=top+1
array[top]=item
}

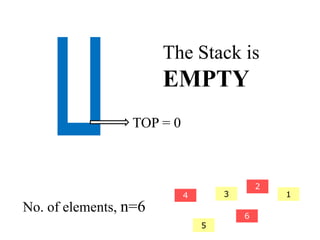
The Stack is
EMPTY
TOP = 0
2
4 3
5
6
1
No. of elements, n=6

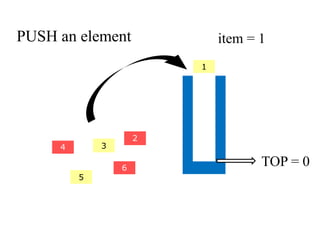
PUSH an element
2
1
4 3
5
item = 1
6 TOP = 0

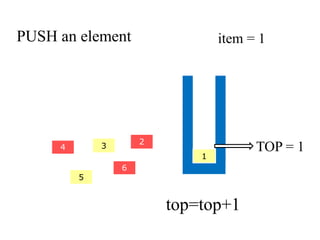
PUSH an element
2
1
4 3
5
6
item = 1
TOP = 1
top=top+1

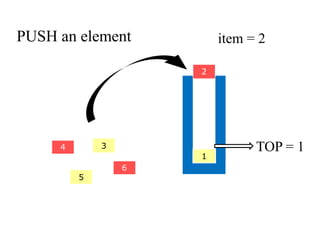
PUSH an element
2
4 3
5
6
1
item = 2
TOP = 1

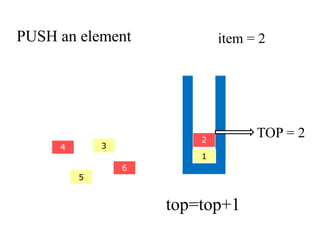
PUSH an element
2
4 3
5
6
1
item = 2
TOP = 2
top=top+1

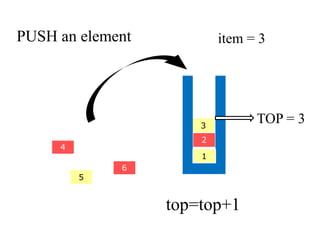
PUSH an element
2
4
3
5
6
1
item = 3
TOP = 3
top=top+1

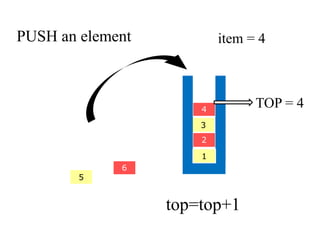
PUSH an element
4
3
2
5
6
1
item = 4
TOP = 4
top=top+1

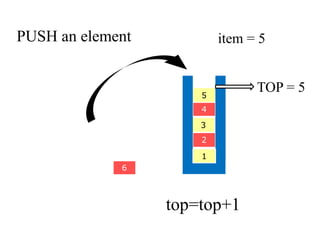
PUSH an element
5
4
3
2
6
1
item = 5
TOP = 5
top=top+1

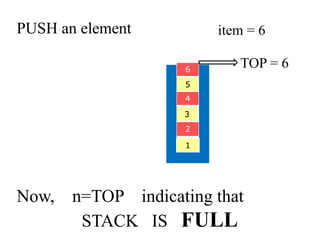
PUSH an element
6
5
4
3
2
1
item = 6
TOP = 6
Now, n=TOP indicating that
STACK IS FULL

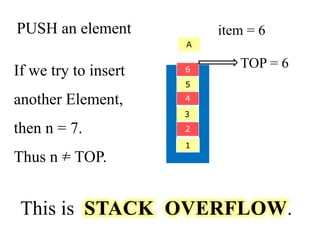
PUSH an element
A
6
5
4
3
2
1
item = 6
TOP = 6
If we try to insert
another Element,
then n = 7.
Thus n = TOP.
This is .

POP ALGORITHM:
pop(array,top,item)
{
if(top=0)
then stack empty
else
item=stack[top]
top=top-1
}

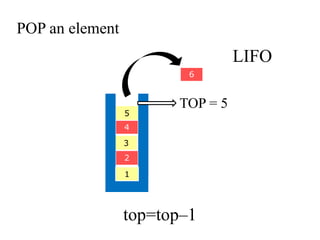
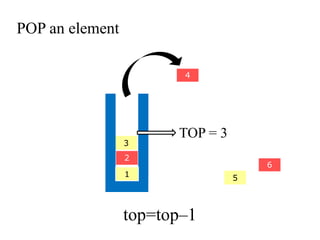
POP an element
5
4
3
2
6
1
TOP = 5
top=top–1
LIFO

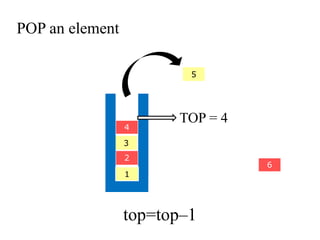
POP an element
4
3
2
5
6
1
TOP = 4
top=top–1

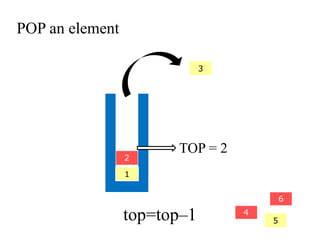
POP an element
2
4
3
5
6
1
TOP = 3
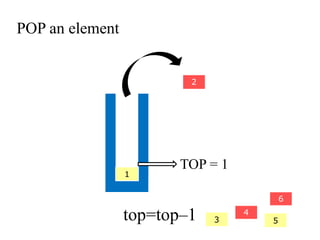
top=top–1

POP an element
2
4
3
5
6
1
TOP = 2
top=top–1

POP an element
2
4
3 5
6
1
TOP = 1
top=top–1

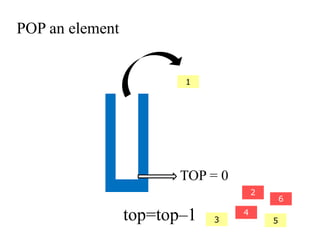
POP an element
2
4
3 5
6
1
TOP = 0
top=top–1

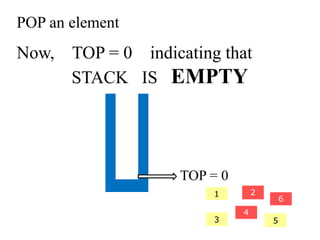
POP an element
Now, TOP = 0 indicating that
2
STACK IS EMPTY
4
TOP = 0
3 5
6
1

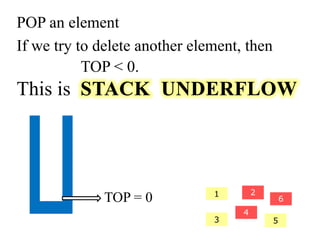
POP an element
If we try to delete another element, then
2
4
3 5
6
TOP < 0.
1 TOP = 0
This is

APPLICATIONS:
 Parentheses checking or matching
 Expression evaluation
 Recursion

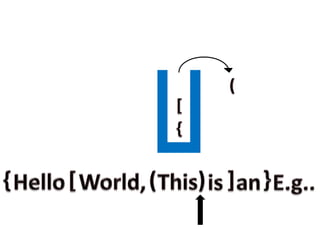
PARENTHESES MATCHING:
It is one of the applications of stack in
which we check for correct matching of
the parentheses in the expression.
It checks for the correct nesting of the
parentheses in the expression.

ALGORITHM:
STEP 1 : Start
STEP 2 : Read the expression in
string format.
STEP 3 : Scan the expression from
left  right.

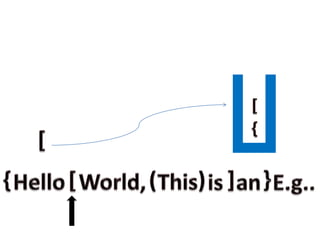
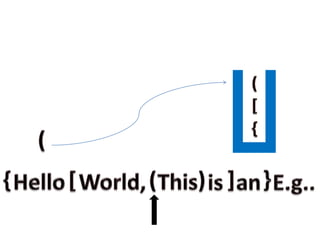
STEP 4 : If any operator or operand is
encountered discard it.
STEP 5 : If left or open parentheses is
encountered PUSH it to the stack.
STEP 6 : If right or closed parentheses is
encountered POP top most element from
the stack.

STEP 7 : Continue the above three steps till
the sentinel character is encountered.
STEP 8 : If the stack is empty print
PARENTHESES MATCHED.
STEP 9 : Else PARENTHESES NOT
MATCHED.
STEP 10 : Stop.

EXAMPLE:
Consider the following expression as
an example.

Here the stack is EMPTY. Then , the
result is
PARENTHESES MATCHED.

If the expression is like below,
or
the stack will NOT be empty. Then,
the result is PARENTHESES NOT
MATCHED.

JUST TRY THIS:
Check the matching of the parentheses in the
following expressions.
 {2*(A–B)]+(A/B)^2}
 (A+B*(C–D)+F])
 (((A+B)*C+D-E)/(F+G)-(H+J)*(K-L))/(M-N)

REFERENCES:
 DATA STRUCTURES , ALGORITHMS AND APPLICATIONS IN C++
(2ND EDITION) – Sartraj sahani
 DATA STRUCTURES AND ALGORITHMS - CONCEPTS,
TECHNIQUES AND APPLICATIONS – G A Vijayalakshmi Pai.
 PROGRAMMING AND DATA STRUCTURES – Ashok N. Kamthane.
 http://davesquared.net/2008/07/brackets-braces-parenthesis-and-other.
html
 http://www.cs.uml.edu/~msheldon/102/2011fall/notes/07_stacks/index
.html
 http://financelab.nctu.edu.tw/DataStructure/lec08.pdf
 http://www.cise.ufl.edu/~sahni/cop3530/slides/lec126.pdf

�ݺ�ߣ

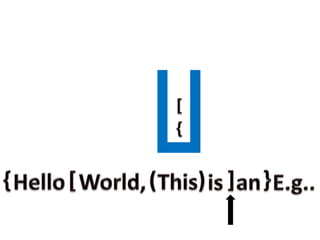
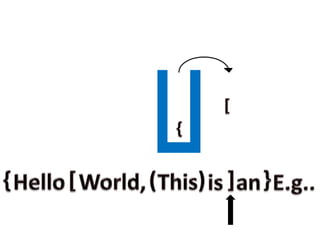
Team 3

More Related Content

Team 3