Teori graf-complete
- 1. TEORI GRAF
- 2. Pendahuluan ’éĪ ’éĪ ’éĪ Graf adalah diagram yang digunakan untuk menggambarkan berbagai struktur yang ada. Contoh : Struktur Organisasi, Peta, Diagram Rangkaian Listrik. Tujuan : Sebagai visualisasi objek-objeknya agar mudah dimengerti.
- 3. Dasar-Dasar Graf (1) ’éĪ Suatu Graf terdiri dari 2 himp. yang berhingga, yaitu himp. titik-titik tak kosong (simbol V(G)) dan himp. garis-garis (simbol E(G)). ’éĪ Setiap garis berhubungan dg satu atau dua titik. Titik-titik tsb disebut Titik Ujung. Garis yang berhubungan dg satu titik disebut Loop. ’éĪ
- 4. Dasar-Dasar Graf (2) ’éĪ Dua garis yang menghubungkan titik yang sama disebut Garis Paralel. ’éĪ Dua titik dikatakan berhubungan bila ada garis yg menghubungkan keduanya. ’éĪ Titik yang tidak punya garis yang berhubungan dengannya disebut Titik Terasing.
- 5. Dasar-Dasar Graf (3) ’éĪ Graf Kosong adalah graf yang tidak punya titik dan garis. ’éĪ Graf Berarah adalah graf yang semua garisnya memiliki arah (Directed Graph / Digraph). ’éĪ Graf Tak Berarah adalah graf yang semua garisnya tidak memiliki arah.
- 6. Contoh 1. ’éĪ Ada 7 kota (A,ŌĆ”,G) yang diantaranya dihubungkan langsung dg jalan darat. Hubungan antar kota didefinisikan sebagai berikut : A terhubung dg B dan D B terhubung dg D C terhubung dg B E terhubung dg F Buatlah graf yang menunjukkan keadaan transportasi di 7 kota tersebut !
- 7. Contoh 2. ’éĪ Gambarlah graf dengan titik-titik dan garis berikut : V(G) = { v1,v2,v3,v4 } E(G) = { e1,e2,e3,e4,e5 } Titik-titik ujung garis adalah : Garis Titik Ujung e1 e2 e3 e4 e5 {v1,v3} {v2,v4} {v1} {v2,v4} {v3}
- 8. Graf Tak Berarah ’éĪ Graf Sederhana adalah graf yang tidak memiliki Loop ataupun Garis Paralel. Contoh 3. ’éĪ Gambarkan semua graf sederhana yang dapat dibentuk dari 4 titik {a,b,c,d} dan 2 garis !
- 9. Graf Tak Berarah ’éĪ Graf Lengkap dengan n titik (simbol Kn) adalah graf sederhana dengan n titik di mana setiap 2 titik yang berbeda selalu dihubungkan dengan suatu garis. ’éĪ Banyaknya garis dalam suatu graf lengkap dengan n titik adalah n( n ŌłÆ1) 2 buah
- 10. Contoh 4. ’éĪ Gambarkan K2 , K3 , K4 , K5 , K6
- 11. Graf Tak Berarah ’éĪ ’éĪ ’éĪ ’éĪ Graf Bipartite adalah graf G yang himp. titiknya/V(G) dapat dibagi menjadi 2 himp yaitu Va dan Vb. Setiap garis dlm G menghubungkan titik di Va dengan titik di Vb. Semua titik dalam Va atau Vb tidak saling berhubungan. Apabila setiap titik di Va berhubungan dengan setiap titik di Vb maka disebut Graf Bipartite Lengkap.
- 12. Komplemen Graf ’éĪ Komplemen suatu graf G (simbol G) dengan n titik adalah suatu graf dengan : 1. Titik-titik G sama dengan titik-titik G. 2. Garis-garis G adalah komplemen garisgaris G terhadap Graf Lengkapnya (Kn) ’éĪ Titik-titik yang dihubungkan dengan garis pada G menjadi tidak terhubung dalam G Sebaliknya, tiitik-titik yang tidak terhubung pada G menjadi terhubung dalam G ’éĪ
- 13. Sub Graf ’éĪ Misalkan G adalah graf. Graf H dikatakan subgraf dari G bila dan hanya bila : 1. V(H) ŌŖå V(G) 2. E(H) ŌŖå E(G) 3. Setiap garis dalam H memiliki titik ujung yang sama dengan garis tersebut dalam G
- 14. Derajat ’éĪ ’éĪ ’éĪ ’éĪ ’éĪ Misal titik v adalah suatu titik dalam graf G. Derajat titik v (simbol d(v)) adalah jumlah garis yang berhubungan dengan titik v. Derajat titik yang berhubungan dengan sebuah loop adalah 2. Derajat total suatu graf G adalah jumlah derajat semua titik dalam G. Derajat total suatu graf selalu genap. Dalam sembarang graf jumlah titik yang berderajat ganjil selalu genap.
- 15. Path dan Sirkuit (1) Misalkan G adalah suatu graf, v0 danvn adalah 2 titik di dalam G. ’éĪ Walk dari titik v0 ke titik vn adalah barisan titik-titik berhubungan dan garis secara berselang-seling diawali dari titik v0 dan diakhiri pada titik vn. ’éĪ Path dari titik v0 ke titik vn adalah walk dari titik v0 ke titik vn yang semua garisnya berbeda. ’éĪ Panjang walk atau path = jumlah garis yang dilalui
- 16. Path dan Sirkuit (2) ’éĪ Path sederhana dari titik v0 ke titik vn adalah path dari titik v0 ke titik vn yang semua titiknya berbeda. ’éĪ Sirkuit adalah path yang dimulai dan diakhiri pada titik yang sama. ’éĪ Sirkuit sederhana adalah sirkuit semua titiknya berbeda kecuali untuk titik awal dan titik akhir.
- 17. Sirkuit Euler (1) ’éĪ Sirkuit Euler adalah sirkuit di mana setiap titik dalam graf G muncul paling sedikit satu kali dan setiap garis muncul tepat satu kali.
- 18. Sirkuit Euler (2) ’éĪ Latar Belakang : Masalah 7 Jembatan yang menghubungkan 4 kota. Apakah mungkin seseorang berjalan mengunjungi kota yang dimulai dan diakhiri pada tempat yang sama dengan melintasi 7 jembatan masing-masing tepat satu kali ? A j1 B j2 j3 j6 j4 D j7 j5 C
- 19. Teorema ’éĪ Graf G memiliki Sirkuit Euler bila dan hanya bila G adalah graf yang terhubung dan semua titik dalam G mempunyai derajat genap.
- 20. Graf Terhubung dan Tidak Terhubung Misalkan G adalah suatu graf ’éĪ 2 titik dalam G ,v1 dg v2 terhubung bila ada walk dari v1 ke v2. ’éĪ Graf G dikatakan ’ü¼ Terhubung ’ā│ setiap 2 titik dalam G terhubung. ’ü¼ Tidak terhubung ’ā│ ada 2 titik dalam G yang tidak terhubung.
- 21. Sirkuit Hamilton ’éĪ Suatu graf terhubung G memiliki Sirkuit Hamilton bila ada sirkuit yang mengunjungi setiap titiknya tepat satu kali (kecuali titik awal dan titik akhir).
- 22. Contoh ’éĪ Gambar di bawah menyatakan peta kota A..G dan jalan-jalan yang menghubungkan kota-kota tsb. Seorang salesman akan mengunjungi tiap kota masing-masing 1 kali dari kota A kembali lagi ke kota A. Carilah rute perjalanan yang harus dilalui salesman tsb ! B j1 j5 j10 A C j2 j9 j4 F E j7 j3 j6 D j11 G j8
- 23. Sirkuit Hamilton vs Euler ’éĪ Perbedaan Sirkuit Euler dengan Sirkuit Hamilton : ’ü¼ Dalam Sirkuit Euler semua garis harus dilalui tepat satu kali, sedangkan semua titiknya boleh dikunjungi lebih dari sekali. ’ü¼ Dalam Sirkuit Hamilton semua titiknya harus dikunjungi tepat satu kali dan tidak harus melalui semua garis.
- 24. Graf Berarah (Digraph) - 1 ’éĪ Contoh graf G berikut : e1 v1 v2 v5 e2 e3 v4 e4 v3 ’éĪ Titik v1 adalah titik awal e1, titik v2 adalah titik akhir e1. Arah garis dari v1 ke v2.
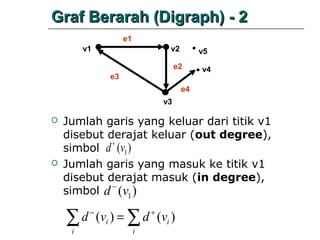
- 25. Graf Berarah (Digraph) - 2 e1 v1 v2 v5 e2 e3 v4 e4 v3 ’éĪ ’éĪ Jumlah garis yang keluar dari titik v1 disebut derajat keluar (out degree), + simbol d (v1 ) Jumlah garis yang masuk ke titik v1 disebut derajat masuk (in degree), simbol d ŌłÆ (v1 ) Ōłæd i ŌłÆ (vi ) = Ōłæ d (vi ) + i
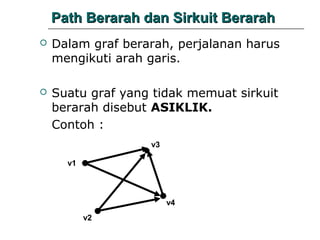
- 26. Path Berarah dan Sirkuit Berarah ’éĪ Dalam graf berarah, perjalanan harus mengikuti arah garis. ’éĪ Suatu graf yang tidak memuat sirkuit berarah disebut ASIKLIK. Contoh : v3 v1 v4 v2
- 27. Contoh ’éĪ Tentukan path berarah terpendek dari titik v5 ke titik v2 ! v1 v5 v3 v2 v7 v4 v8 v6
- 28. Pohon (Tree) ’éĪ ’éĪ ’éĪ Struktur Pohon adalah salah satu kasus dalam graf. Penerapannya pada Teori Struktur Data. Graf G disebut Pohon ’ā│ G merupakan graf sederhana yang tidak memuat sirkuit dan terhubung.
- 29. Pohon (2) ’éĪ ’éĪ Daun adalah titik di dalam Pohon yang berderajat 1. Titik dalam Pohon yang berderajat > 1 disebut Titik Cabang. Teorema Suatu pohon dengan n titik memiliki (n-1) garis
- 30. Pohon Rentang ’éĪ Pohon Rentang dari graf terhubung G adalah subgraf G yang merupakan pohon dan memuat semua titik dalan G.
- 31. Contoh ’éĪ Cari pohon rentang dari graf G ! v2 v1 v3 v7 v4 v5 v8 v6
- 32. Graf Berlabel ’éĪ ’éĪ ’éĪ ’éĪ Graf Berlabel : graf tanpa garis paralel yang setiap garisnya berhubungan dengan bilangan riil positif yang menyatakan bobot garis tersebut. Simbol : w(e). Total Bobot : jumlah bobot semua garis dalam graf. Bobot suatu garis dapat mewakili ŌĆ£jarakŌĆØ, ŌĆ£biayaŌĆØ, ŌĆ£panjangŌĆØ, ŌĆ£kapasitasŌĆØ, dll.
- 33. Pohon Rentang Minimum ’éĪ Masalah : mencari pohon rentang dengan total bobot seminimal mungkin. ’éĪ Metode : Algoritma Kruskal
- 34. Algoritma Kruskal (1) ’éĪ Mula-mula urutkan semua garis dalam graf dari yang bobotnya terkecil sampai terbesar. ’éĪ G : graf mula-mula dg n titik, T : Pohon Rentang Minimum, E : himpunan semua garis dlm G ’éĪ ’éĪ
- 35. Algoritma Kruskal (2) Algoritma : Isi T dengan semua titik dalam G tanpa garis. m=0 Selama m < (n-1) lakukan : 1. 2. 3. a. b. c. Pilih garis e dalam E dg bobot terkecil. Jika ada beberapa garis, pilih salah satu. Hapus garis e dari E. Jika garis e ditambahkan ke T tidak menghasilkan sirkuit, maka I. Tambahkan e ke T. II. m = m+1 (Nilai m dinaikkan satu).
- 36. Lintasan Terpendek ’éĪ ’éĪ Mencari path dengan total bobot paling minimal dari sebuah graf berlabel. Metode : Algoritma Djikstra
- 37. Algoritma Djikstra V L(j) w(i,j) T = = = = {v1, v2, ŌĆ”, vn} ’āĀ titik awal : v1, titik akhir : vn jumlah bobot lintasan terpendek dari v1 ke vj bobot garis dari titik v1 ke titik vj himp. titik yg sudah terpilih dlm alur lintasan terpendek ALGORITMA 1. T={} L(v1) = 0 L(v2) = L(v3) = ŌĆ” = L(vn) = ~
- 38. Algoritma Djikstra 2. 3. Selama vn Ōłē T lakukan : a. Pilih titik vk Ōłł V ŌĆō T dengan L(vk) terkecil T = T Ōł¬ { vk } b. Untuk setiap vj Ōłł V ŌĆō T hitung : L(vj) = min[ L(vj) , L(vk) + w(vk,vj) ] Telusuri alur path minimum mulai dari titik akhir (vn) sampai titik awal (v1)




































![Algoritma Djikstra
2.
3.
Selama vn Ōłē T lakukan :
a. Pilih titik vk Ōłł V ŌĆō T dengan L(vk) terkecil
T = T Ōł¬ { vk }
b. Untuk setiap vj Ōłł V ŌĆō T hitung :
L(vj) = min[ L(vj) , L(vk) + w(vk,vj) ]
Telusuri alur path minimum mulai dari titik akhir
(vn) sampai titik awal (v1)](https://image.slidesharecdn.com/teori-graf-complete-140308084811-phpapp02/85/Teori-graf-complete-38-320.jpg)