Finding motivations behind message interaction in MDT
- 1. MOTIVATIONS BEHIND SENDING MESSAGES IN MDT. (METHODS, DERIVATION & RESULTS) Anup Sawant SONIC @ Northwestern University
- 2. Acknowledgement Ī¦?? This analysis wouldnĪ»t have been possible without the support of SONIC @ Northwestern University and DELTA Lab @ Georgia Tech in developing the project Ī«My Dream TeamĪ». Ī¦?? Other project members: ĪĶ?? Dr. Noshir Contractor, Northwestern University. ĪĶ?? Dr. Leslie DeChurch, Georgia Tech. ĪĶ?? Dr. Edward Palazzolo, Northwestern University. ĪĶ?? Harshad Gado, Northwestern University. ĪĶ?? Amy Wax, Georgia Tech. ĪĶ?? Samuel Posnock, Georgia Tech. ĪĶ?? Peter Seely, Georgia Tech.
- 3. Overview Ī¦?? Description ĪĶ?? Objective ĪĶ?? Corpus details Ī¦?? Methodology ĪĶ?? Different approaches ĪĶ?? Text Parsing ĪĶ?? Forming vectors ĪĶ?? Measuring similarity ĪĶ?? K-Means ĪĶ?? Choosing the optimum K ĪĶ?? Distribution & Density ĪĶ?? Topic Indicators Ī¦?? Results ĪĶ?? What can we infer ? ĪĶ?? Supporting inference ĪĶ?? Gratitude & Request ĪĶ?? Need, Liking, Invite & Praise ĪĶ?? Collaboration & Grouping Ī¦?? Conclusion
- 4. Project Description Ī¦?? Objective ĪĶ?? To do textual analysis and find motivations behind message interaction in the process of forming teams. ĪĶ?? Serve as a proof for some of the known reasons about team formation ties, through, mathematically derived topical patterns hidden in unstructured text data. Ī¦?? Corpus details ĪĶ?? Ī«My Dream TeamĪ» run 19th ©C 23rd Feb, 2014. ĪĶ?? # Students participated : 214 ĪĶ?? # Text messages exchanged : 353 ĪĶ?? # Unique words/terms in entire corpus : 619
- 5. Methodology/Different Approaches Ī¦?? Problem statement : Ī░ Given a text corpus X = { x1, x2, x3ĪŁ.} Where xi = document/message, find the topics/ideas (in our context, primary motivations) that represent individual clusters within X.Ī▒ Ī¦?? Possible Approaches : ĪĶ?? Latent Semantic Analysis (mostly used in IR for indexing) ĪĶ?? Latent Dirichlet Allocation (probabilistic topic modeling) ĪĶ?? Document Clustering (we go by this) Ī¦?? Problems : ĪĶ?? Real world textual data is always Ī░dirtyĪ▒ when it comes to text parsing. ĪĶ?? Performance and accuracy can depend on rich vocabulary for grammatical parsing.
- 6. Methodology/Text Parsing Ī░I enjoy learning and growing while also getting out a little of my competitive spirit.Ī▒ Ī░i enjoy learning and growing while also getting out a little of my competitive spirit.Ī▒ [i, enjoy, learn, and, grow, while, also, get, out, a, little, of, my, competitive, spirit] [i, enjoy, learn, grow, out, little, my, competitive, spirit] Lowercase Lemmatize ©C remove punctuations, split into words & convert each word to its root. Remove Stopwords
- 7. Methodology/Forming Vectors Ī¦?? Bag of words : Collect all unique words from the corpus vocabulary. Ī¦?? Document-Term index : For each word in the vocabulary, count its frequency across all documents/messages in the corpus. (example below) Term/Word Message -1 Message-2 Message-3 Message-4 hey 1 1 1 0 team 1 1 0 1 join 1 0 1 1 work 1 0 1 0
- 8. Methodology/Measuring Similarity Ī¦?? Cosine Similarity : Performs better when compared to Euclidean measure. Similarity is mostly retained irrespective of vectors space distance due to length of vectors. Intuitively, documents/messages dealing with same topic/domain remain close in vector space irrespective of their message length. Euclidean distance Cosine distance ”© x y (0,0) Message 1 Message 2 Example : The figure on right indicates 2 message vectors. Although, the Euclidean measure shows quite a bit of distance in vector space, the Cosine measure indicates that the vectors are close enough to point in the same direction. Cos 0 = 1 indicates similar vectors, Cos 90 = 0 indicates dissimilar vectors.
- 9. Methodology/K-Means Ī¦?? The K-means algorithm is a method to automatically cluster similar data examples together. The intuition behind K-means is an iterative procedure that starts by guessing the initial centroids, and then refines this guess by repeatedly assigning examples to their closest centroids and then recomputing the centroids based on the assignments. Img source- Wikipedia
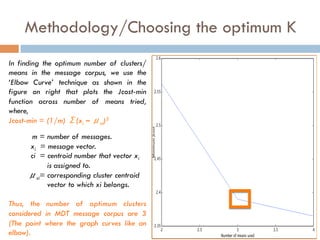
- 10. Methodology/Choosing the optimum K In finding the optimum number of clusters/ means in the message corpus, we use the Ī«Elbow CurveĪ» technique as shown in the figure on right that plots the Jcost-min function across number of means tried, where, Jcost-min = (1/m) ”▓(xi ©C ”╠ci)2 m = number of messages. xi = message vector. ci = centroid number that vector xi is assigned to. ”╠ci= corresponding cluster centroid vector to which xi belongs. Thus, the number of optimum clusters considered in MDT message corpus are 3 (The point where the graph curves like an elbow).
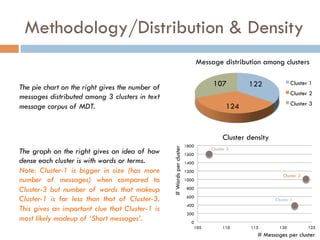
- 11. Methodology/Distribution & Density 122 124 107 Message distribution among clusters Cluster 1 Cluster 2 Cluster 3 0 200 400 600 800 1000 1200 1400 1600 1800 105 110 115 120 125 #Wordspercluster # Messages per cluster Cluster density Cluster 3 The pie chart on the right gives the number of messages distributed among 3 clusters in text message corpus of MDT. Cluster 2 Cluster 1 The graph on the right gives an idea of how dense each cluster is with words or terms. Note: Cluster-1 is bigger in size (has more number of messages) when compared to Cluster-3 but number of words that makeup Cluster-1 is far less than that of Cluster-3. This gives an important clue that Cluster-1 is most likely madeup of Ī«Short messagesĪ».
- 12. Methodology/Topic indicators On a broader scale we already know that all the messages deal with Ī«Team FormationĪ» topic. We are on a hunt to find the hidden motivations on a sub- topical scale. The segmented pyramid on the right shows some of the top ranking words by frequency in each cluster so far with the core topic as Ī«Team FormationĪ». The words that are most common to all clusters and reflect Ī«Team FormationĪ» topic on a broader scale, are at the core of the pyramid. We consider top words as strong indicators of hidden motivations. Cluster-2 # messages : 124 # words : 1013 Cluster-3 # messages : 107 # words : 1601 Cluster-1 # messages : 122 # words : 387
- 13. Methodology/What can we infer ? Cluster-1: Has short messages indicating gratitude or request to be a member through words like Ī«thanksĪ» and Ī«acceptĪ». Low frequency words from this cluster are mostly a slang or non-dictionary word. Cluster-2: Has messages that mostly refer recipient's qualities and hence words like Ī«coolĪ» & Ī«likeĪ» stand out as some of the top words. Probably, these messages also talk about sender's Ī«needĪ» to add one or more member to the team. Cluster-3: Has messages that indicate topics such as working together, grouping and mostly collaboration with words like Ī«groupĪ», Ī«workĪ» and Ī«togetherĪ». with high frequency. Cluster-2 # messages : 124 # words : 1013 Cluster-3 # messages : 107 # words : 1601 Cluster-1 # messages : 122 # words : 387
- 14. Results/Supporting inference Ī¦?? Though top words provide a strong indication of probable topics in a cluster, high frequency of each word isnĪ»t enough to support our assumption of topics. Ī¦?? A good support to our inference would be through a mathematical analysis of co-occurrence of the top words from each cluster with the words Ī«teamĪ» and Ī«youĪ» that makeup the core topic of Ī«Team FormationĪ».
- 15. Results/Probability for coherence Ī¦?? Example : Ī░Ana (a word) is in the mall (topic) given her best friends Harry and Brian (Ī«teamĪ» & Ī«youĪ») are in the mall (topic).Ī▒ Ī¦?? In other words, a word would define a topic only if it co-occurs with other supporting words to reflect coherence necessary to define that topic. Ī¦?? P(topic) = P(w/X) where, w = word, X = core words of topic Ī«Team FormationĪ». Ī¦?? We calculate P(topic) across all clusters for a given word.
- 16. Results/Gratitude & Request by Cluster 1 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 thanks accept Probability words Topic probability through conditional probability of words given core Team Formation words Ī«teamĪ» and Ī«youĪ» Cluster 1 Cluster 2 Cluster 3
- 17. Results/Need, Liking, Invite & Praise by Cluster 2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 need one like join cool Probability words Topic probability through conditional probability of words given core Team Formation words Ī«teamĪ» and Ī«youĪ» Cluster 1 Cluster 2 Cluster 3
- 18. Results/Collaboration & Grouping by Cluster 3 0 0.05 0.1 0.15 0.2 0.25 0.3 work group together Probability words Topic probability through conditional probability of words given core Team Formation words Ī«teamĪ» and Ī«youĪ» Cluster 1 Cluster 2 Cluster 3
- 19. Conclusion Ī¦?? Document clustering with probabilistic support to topical inference over message corpus of MDT has helped us expose following motivations behind sending messages. Users interacted when, ĪĶ?? There was a need for one or more person to complete the team. ĪĶ?? They liked someoneĪ»s profile. ĪĶ?? They wanted to invite someone to join their team. ĪĶ?? They wanted to praise someone for good profile or looks. ĪĶ?? They wanted to group/merge their incomplete teams. ĪĶ?? They wanted to collaborate/work with someone. ĪĶ?? They wanted to express gratitude. ĪĶ?? They wanted to earnestly request someone to join.






![Methodology/Text Parsing
Ī░I enjoy learning and growing while also getting out a little of my competitive
spirit.Ī▒
Ī░i enjoy learning and growing while also getting out a little of my competitive
spirit.Ī▒
[i, enjoy, learn, and, grow, while, also, get, out, a, little, of, my, competitive, spirit]
[i, enjoy, learn, grow, out, little, my, competitive, spirit]
Lowercase
Lemmatize ©C remove punctuations, split
into words & convert each word to its
root.
Remove Stopwords](https://image.slidesharecdn.com/textualanalysis-140331134654-phpapp01/85/Finding-motivations-behind-message-interaction-in-MDT-6-320.jpg)