The non-overlapping constraint between objects described by non-linear inequalities
- 1. The non-overlapping constraint between objects described by non-linear inequalities Ignacio SALAS & Gilles CHABERT & Alexandre GOLDSZTEJN
- 2. Content Motivation Conclusions Introduction The Algorithm I. Salas & G. Chabert & A. Goldsztejn Experimental Results Overlapping as a Minkowski sum
- 3. Motivation I. Salas & G. Chabert & A. Goldsztejn 1 / 23 Which are the positions and orientations of an object such that it does not overlap a second (fixed) one? A key question in the packing problem
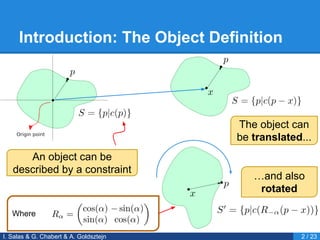
- 4. Introduction: The Object Definition I. Salas & G. Chabert & A. Goldsztejn 2 / 23 The object can be translated... Where ŌĆ”and also rotated An object can be described by a constraint
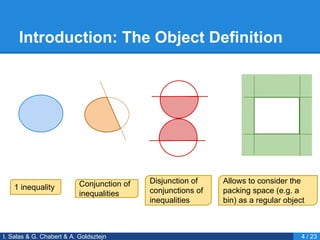
- 5. Introduction: The Object Definition I. Salas & G. Chabert & A. Goldsztejn 3 / 23 ŌŚÅ We consider objects that can be represented by a non-linear inequality ŌŚÅ And our results carry over the more general case of first order formulas Disjunctions of conjunctions of inequalities
- 6. Introduction: The Object Definition I. Salas & G. Chabert & A. Goldsztejn 4 / 23 1 inequality Conjunction of inequalities Disjunction of conjunctions of inequalities Allows to consider the packing space (e.g. a bin) as a regular object
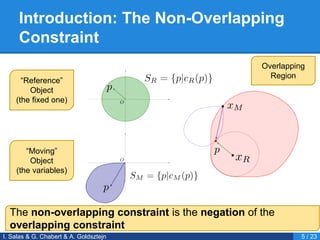
- 7. Introduction: The Non-Overlapping Constraint I. Salas & G. Chabert & A. Goldsztejn 5 / 23 ŌĆ£ReferenceŌĆØ Object (the fixed one) ŌĆ£MovingŌĆØ Object (the variables) Overlapping Region The non-overlapping constraint is the negation of the overlapping constraint
- 8. Introduction: The Non-Overlapping Constraint I. Salas & G. Chabert & A. Goldsztejn 6 / 23 Overlapping Constraint The position of the moving object is the variable of the system Considering the rotation angle
- 9. Introduction: The Non-Overlapping Constraint I. Salas & G. Chabert & A. Goldsztejn 7 / 23 The overlapping region considering only translation, takes the following form ŌĆ” and considering also rotation
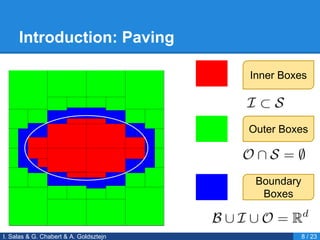
- 10. Introduction: Paving Outer Boxes Inner Boxes Boundary Boxes I. Salas & G. Chabert & A. Goldsztejn 8 / 23
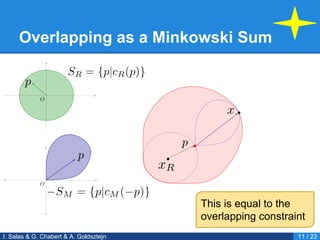
- 11. Overlapping as a Minkowski Sum I. Salas & G. Chabert & A. Goldsztejn 9 / 23 What is the Minkowski Sum? If the sets are described by constraints
- 12. Overlapping as a Minkowski Sum I. Salas & G. Chabert & A. Goldsztejn 10 / 23 Comparing ŌĆ” and ŌĆ” leads to
- 13. Overlapping as a Minkowski Sum I. Salas & G. Chabert & A. Goldsztejn 11 / 23 This is equal to the overlapping constraint
- 14. Overlapping as a Minkowski Sum In the case of rotation, we consider ŌĆ£augmentedŌĆØ objects I. Salas & G. Chabert & A. Goldsztejn 12 / 23
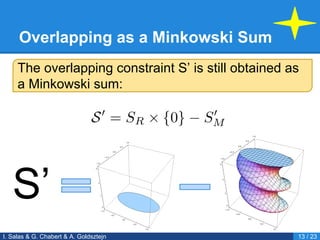
- 15. Overlapping as a Minkowski Sum The overlapping constraint SŌĆÖ is still obtained as a Minkowski sum: SŌĆÖ I. Salas & G. Chabert & A. Goldsztejn 13 / 23
- 16. The Algorithm Inner contraction Outer rejection test Bisection I. Salas & G. Chabert & A. Goldsztejn 14 / 23 The process stops when the surface of the unknown region B is less than % of the initial box [x] ŌŚÅ Our objective is to calculate a paving of the overlapping region ŌŚÅ our algorithm is based on a classical branch & prune algorithm and makes use of the Minkowski sum The central operation can be broken into 3 steps: [x]
- 17. The Algorithm: Inner Contractor I. Salas & G. Chabert & A. Goldsztejn 15 / 23 Given that Let us consider How can we find a subbox of [x] that is inside S? Then Before describing how to contract a box [x] ... with
- 18. The Algorithm: Inner Contractor I. Salas & G. Chabert & A. Goldsztejn 16 / 23 The resulting box is used in a sweep loop must respect
- 19. The Algorithm: Inner Contractor I. Salas & G. Chabert & A. Goldsztejn 17 / 23 The Sweep loop At each step the point is ŌĆ£inflatedŌĆØ to the box These boxes are pilled up until some face is covered
- 20. The Algorithm: Outer rejection test I. Salas & G. Chabert & A. Goldsztejn 18 / 23 If this assertion holds, the whole box is marked as outer Moving Object Reference Object
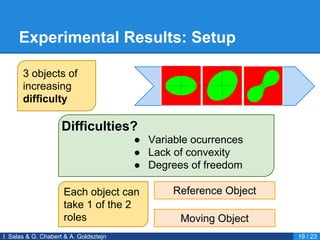
- 21. Experimental Results: Setup I. Salas & G. Chabert & A. Goldsztejn 19 / 23 ŌŚÅ Variable ocurrences ŌŚÅ Lack of convexity ŌŚÅ Degrees of freedom Difficulties? 3 objects of increasing difficulty Each object can take 1 of the 2 roles Reference Object Moving Object
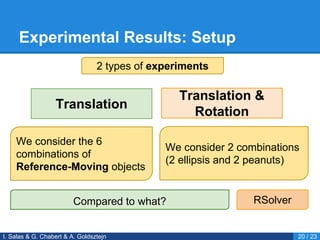
- 22. Experimental Results: Setup I. Salas & G. Chabert & A. Goldsztejn 20 / 23 Translation Translation & Rotation We consider the 6 combinations of Reference-Moving objects We consider 2 combinations (2 ellipsis and 2 peanuts) 2 types of experiments Compared to what? RSolver
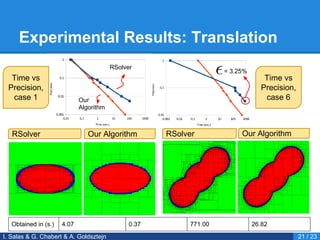
- 23. Experimental Results: Translation I. Salas & G. Chabert & A. Goldsztejn 21 / 23 Time vs Precision, case 1 Time vs Precision, case 6 RSolver Our Algorithm RSolver Our Algorithm Obtained in (s.) 4.07 0.37 771.00 26.82 RSolver Our Algorithm = 3.25%
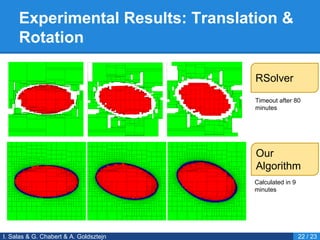
- 24. Experimental Results: Translation & Rotation I. Salas & G. Chabert & A. Goldsztejn 22 / 23 RSolver Our Algorithm Timeout after 80 minutes Calculated in 9 minutes
- 25. Conclusions I. Salas & G. Chabert & A. Goldsztejn 23 / 23 We give an efficient way to calculate a guaranteed approximation of the non-overlapping constraint. The efficiency is measured with respect to the time required for solving the quantified constraints directly. In future works, we will try to solve the full packing problem using our results on the non-overlapping constraints.
- 26. ??
- 27. The non-overlapping constraint between objects described by non-linear inequalities Ignacio SALAS & Gilles CHABERT & Alexandre GOLDSZTEJN
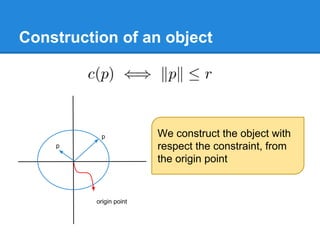
- 28. Construction of an object origin point p p We construct the object with respect the constraint, from the origin point
- 29. Obtaining the augmented set SŌĆÖm
- 30. Conclusions: Future work I. Salas & G. Chabert & A. Goldsztejn 23 We will try to solve the full packing problem using our results on the non-overlapping constraints. Also, we want to know whether it is possible find a quick inner test.
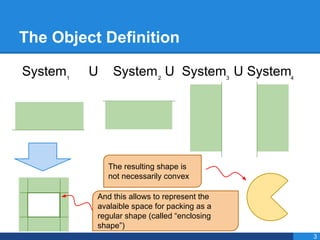
- 31. The Object Definition System U System U System U System1 2 3 4 The resulting shape is not necessarily convex And this allows to represent the avalaible space for packing as a regular shape (called ŌĆ£enclosing shapeŌĆØ) 3
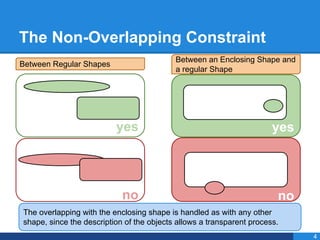
- 32. The Non-Overlapping Constraint The overlapping with the enclosing shape is handled as with any other shape, since the description of the objects allows a transparent process. 4 yes no no yes Between Regular Shapes Between an Enclosing Shape and a regular Shape
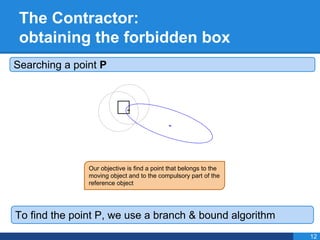
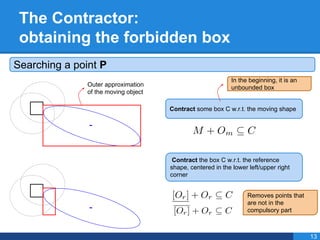
- 33. The Contractor: obtaining the forbidden box Searching a point P To find the point P, we use a branch & bound algorithm 12 Our objective is find a point that belongs to the moving object and to the compulsory part of the reference object
- 34. The Contractor: obtaining the forbidden box Searching a point P Contract some box C w.r.t. the moving shape Contract the box C w.r.t. the reference shape, centered in the lower left/upper right corner 13 In the beginning, it is an unbounded box Removes points that are not in the compulsory part Outer approximation of the moving object
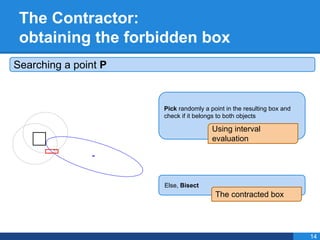
- 35. The Contractor: obtaining the forbidden box Searching a point P Pick randomly a point in the resulting box and check if it belongs to both objects Else, Bisect The contracted box Using interval evaluation 14
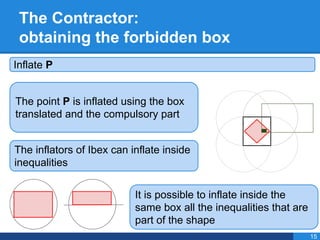
- 36. The Contractor: obtaining the forbidden box Inflate P The point P is inflated using the box translated and the compulsory part The inflators of Ibex can inflate inside inequalities It is possible to inflate inside the same box all the inequalities that are part of the shape 15
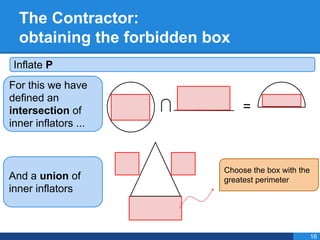
- 37. The Contractor: obtaining the forbidden box Inflate P For this we have defined an intersection of inner inflators ... = And a union of inner inflators Choose the box with the greatest perimeter 16
- 38. The Contractor: obtaining the forbidden box Hence, it is possible to construct a box B inside the compulsory part of the reference object, i.e.
- 39. The Contractor: overlapping shape ŌŚÅ The overlapping shape is the region where the reference shape will always collide with the moving shape. ŌŚÅ Can be calculated exactly with polytopes, but we are using curved objects. We calculate something different 17
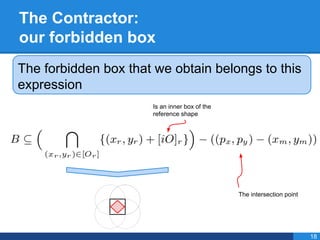
- 40. The Contractor: our forbidden box Is an inner box of the reference shape The intersection point The forbidden box that we obtain belongs to this expression 18
- 41. Inner Contractor Reference Shape Moving Shape Domain of the origin of the moving shape (to be contracted) ŌŚÅ Target: Remove all the parts that violate the non-overlapping constraint ŌŚÅ The contraction operates over 2 shapes ŌŚŗ The reference shape ŌŚŗ The moving shape 7
- 42. The Contractor O1 ES O2 O3 O4 O2 ES O1 O3 O4 O3 ES O1 O2 O4 O4 ES O1 O2 O3 List of moving shapes List of reference shapes The origin box of each moving shape is contracted with Sweep. Enclosing Shape 8
- 43. Considering that the forbidden box must ŌŚÅ ŌĆ£extendŌĆØ an initial forbidden point M ŌŚÅ be included inside a ŌĆ£working areaŌĆØ (WA) The Contractor: obtaining the forbidden box How to do it? ŌŚÅ Sweep requires the ability of calculating a forbidden box with respect to each constraint ŌŚÅ No algorithm exists so far for the non-overlapping constraint The current domain in the context of the sweep loop 9
- 44. Satisfiability Check To find this point, was used a branch & bound algorithm Contract some box with the moving shape Contract the reference shape centered in the some point Evaluate the intersection in a random point of the resulting box Else, Bisect The satisfiability check works similar to the point selector, but only evaluate if the point exists
- 45. Sweep ŌŚÅ The target of the sweep algorithm is to prune all the parts of some domain that violate some constraint ŌŚÅ To perform this, we must ŌĆ£saturateŌĆØ one of the dimensions with forbidden boxes ŌŚÅ This forbidden boxes must consider some forbidden point and the working area










![The Algorithm
Inner contraction
Outer rejection test
Bisection
I. Salas & G. Chabert & A. Goldsztejn 14 / 23
The process stops when the surface of the unknown region B
is less than % of the initial box [x]
ŌŚÅ Our objective is to calculate a paving of the overlapping
region
ŌŚÅ our algorithm is based on a classical branch & prune
algorithm and makes use of the Minkowski sum
The central
operation can
be broken into
3 steps:
[x]](https://image.slidesharecdn.com/thenon-overlappingconstraintbetweenobjectsdescribedbynon-linearinequalities-140718171152-phpapp02/85/The-non-overlapping-constraint-between-objects-described-by-non-linear-inequalities-16-320.jpg)
![The Algorithm: Inner Contractor
I. Salas & G. Chabert & A. Goldsztejn 15 / 23
Given that
Let us consider
How can we find a subbox of [x] that is inside S?
Then
Before describing how to contract a box [x] ...
with](https://image.slidesharecdn.com/thenon-overlappingconstraintbetweenobjectsdescribedbynon-linearinequalities-140718171152-phpapp02/85/The-non-overlapping-constraint-between-objects-described-by-non-linear-inequalities-17-320.jpg)