Three Uses for Truth Tables
- 1. Three Uses for Truth Tables
- 2. Checking for Contingency • A sentence that is true no matter the truth values of the parts is tautological. • A sentence that is false no matter the truth values of the parts is contradictory. • A sentence that might be true or might be false depending on the truth values of its parts is contingent. • Since a truth table is a convenient way of listing all the possibilities for component sentences, it allows a rapid determination of a sentence’s status as tautological, contradictory, or contingent.
- 3. Truth-Table Test for Contingency A B B (B A) T T F T T T F T T T F T F T F F F T T T Since all the values under the main connective (the left horseshoe) are T, this table shows that the sentence B (B A) is a tautology.
- 4. Checking for Equivalence • When two sentences have the same truth value no matter what the values of the component parts are, the sentences are equivalent. • Each of the rows on the truth table represents a way the world could be. If there is no way the world could be that gives two sentences different truth values, then they are truth- functionally the same.
- 5. Truth-Table Test for Equivalence A B A B A B T T T F T T F F F F F T T T T F F T T T This table shows that A B is equivalent to A B. Since the column under the conditional and the column under the disjunction are the same on every row, it is not possible for the sentences to differ in truth value.
- 6. Checking for Validity • Remember that in a valid argument it is impossible to have all true premises and a false conclusion. • Since a truth table is a convenient way of listing all the possibilities, it can tell us at a glance whether it is possible for an argument to have all true premises and a false conclusion. • If no row of the table has each premise true and the conclusion false then the argument is valid. If there is at least one row with all true premise and a false conclusion then the argument is invalid.
- 7. Truth Table Test for Validity A B A B B ∴ A T T T F F T F F T F F T T F T F F T T T Since no row has all true premises and a false conclusion the argument is valid. The only row with all true premises is the bottom row and on that row the conclusion is true. The important thing is not that there’s a row with all true premises and a true conclusion but rather that there’s no row with all true premises and a false conclusion.
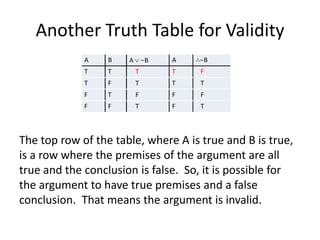
- 8. Another Truth Table for Validity A B A B A ∴ B T T T T F T F T T T F T F F F F F T F T The top row of the table, where A is true and B is true, is a row where the premises of the argument are all true and the conclusion is false. So, it is possible for the argument to have true premises and a false conclusion. That means the argument is invalid.