Tokyo conference
Download as pptx, pdf0 likes824 views
The document proposes a new multi-parent crossover operator for genetic algorithms. It selects four parents and creates two offspring by finding the midpoints between parents 1-2 and 3-4, then using difference vectors to determine discovery areas bounded by the parents from which to sample offspring values. The operator aims to maintain diversity better than BLX and UNDX operators while still converging efficiently. It is tested on single-objective and multi-objective problems, showing better optimization performance than the other operators.
![Introduction
? The Genetic Algorithms(GA) is popular optimization method to solve
single-objective and multi-objective optimization problem
? GA have three main operator, such as, Selection, Crossover and
mutation
? Crossover operator is the main operator for GA performance
? The popular Crossover operator is BLX and UNDX Algorithm[1]
? The GA is popular in aerospace engineering, such as, to increase the
efficiency of aircraft, to used for the navigation of aircraft, or to
reduce the weight of the aircraft weight, etc.
[1] Hajime K, Isao O and Shigenobu K. Theoretical Analysis of the Unimodal Normal Distribution Crossover for Real-coded
Genetic Algorithms. Transactions of the Society of Instrument & Control Engineers, 2002, 2(1), 187-194
3](https://image.slidesharecdn.com/tokyoconference-140324000423-phpapp01/85/Tokyo-conference-3-320.jpg)
![Non-dominated Sorting Genetic Algorithm (NSGA-II)
? Crowding distance assignment
? Individuals are sorted in each objective domain
? The first individual and the last individual in the rank are assigned
the crowding distance equal to infinity
? For the other individuals, the crowding distance is calculated by
?? =
?=1
?
??
??+1
?
? ??
???1
?
??
???
? ??
???
? [2, ? ? 1]
? Niche comparison
? < ? ? ?? ? ???? < ? ????
?? ((? ???? = ? ????) ??? (? ???????? > ? ????????))
? Between two solution with differing non-domination ranks the
solution with the better rank is preferred
? If both solutions belong to the same front, the solution which is
located in lesser crowed region is preferred.
6](https://image.slidesharecdn.com/tokyoconference-140324000423-phpapp01/85/Tokyo-conference-6-320.jpg)
Tokyo conference
- 1. New Multi-parent Crossover based on Crossing Two Segments Bounded by Selected Parents Atthaphon Ariyarit, Kanazaki Masahiro Department of Aerospace Engineering, Graduate School of System Design, Tokyo Metropolitan University 6MӋѧо 2014/03/07
- 2. Outline ? Introduction ? Objective ? Overview of Popular Crossover Operators ? Blended Crossover (BLX) ? Unimodal Normal Distribution Crossover (UNDX) ? New Multi-parent Crossover Method ? Test Problems ? Single-objective optimization problems ? Multi-objective optimization problems ? Multi-objective airfoil optimization problem ? Results ? Conclusions 2
- 3. Introduction ? The Genetic Algorithms(GA) is popular optimization method to solve single-objective and multi-objective optimization problem ? GA have three main operator, such as, Selection, Crossover and mutation ? Crossover operator is the main operator for GA performance ? The popular Crossover operator is BLX and UNDX Algorithm[1] ? The GA is popular in aerospace engineering, such as, to increase the efficiency of aircraft, to used for the navigation of aircraft, or to reduce the weight of the aircraft weight, etc. [1] Hajime K, Isao O and Shigenobu K. Theoretical Analysis of the Unimodal Normal Distribution Crossover for Real-coded Genetic Algorithms. Transactions of the Society of Instrument & Control Engineers, 2002, 2(1), 187-194 3
- 4. Introduction ? Procedure of Genetic Algorithms ? Genetic operator such as selection, crossover and mutation are applied to the parent to create the offspring ? BLX and UNDX cannot always maintain high diversity ? For real world problem, the algorithm that can maintain higher diversity, good convergence rate while it shows 4
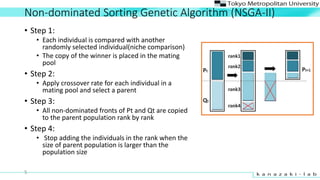
- 5. Non-dominated Sorting Genetic Algorithm (NSGA-II) ? Step 1: ? Each individual is compared with another randomly selected individual(niche comparison) ? The copy of the winner is placed in the mating pool ? Step 2: ? Apply crossover rate for each individual in a mating pool and select a parent ? Step 3: ? All non-dominated fronts of Pt and Qt are copied to the parent population rank by rank ? Step 4: ? Stop adding the individuals in the rank when the size of parent population is larger than the population size 5
- 6. Non-dominated Sorting Genetic Algorithm (NSGA-II) ? Crowding distance assignment ? Individuals are sorted in each objective domain ? The first individual and the last individual in the rank are assigned the crowding distance equal to infinity ? For the other individuals, the crowding distance is calculated by ?? = ?=1 ? ?? ??+1 ? ? ?? ???1 ? ?? ??? ? ?? ??? ? [2, ? ? 1] ? Niche comparison ? < ? ? ?? ? ???? < ? ???? ?? ((? ???? = ? ????) ??? (? ???????? > ? ????????)) ? Between two solution with differing non-domination ranks the solution with the better rank is preferred ? If both solutions belong to the same front, the solution which is located in lesser crowed region is preferred. 6
- 7. Objective ? Development efficient crossover operator for real world problem ? Investigation of the proposed crossover operator by solving the single-objective optimization problem, multi-objective optimization problem and for the real world problem 7
- 8. BLX Operator ? BLX is a crossover operator for real code GA ? BLX created two offspring from two parents by use following equation ?? (1,?+1) = ?? ?? 1,? + 1 ? ?? ?? (2,?) ?? (2,?+1) = 1 ? ?? ?? 1,? + ?? ?? (2,?) where ?? = 1 + 2 ?? ? ? and = 0.5 ? This is called BLX-0.5 Center pointOffspring1 Offspring2Parent1 Parent2 Possible crossover region 8 d d d
- 9. UNDX operator ? UNDX crossover is a crossover operator for real code Genetic Algorithms ? UNDX is a multi-parent crossover operator ? UNDX is operator based on the normal distribution 9
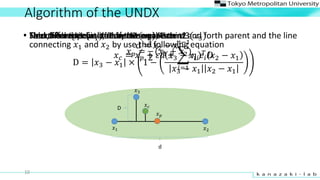
- 10. Algorithm of the UNDX ? ? ?2?1 ?3 10 ? Select Parent1 (?1), Parent2 (?2), Parent3(?3)? Find the midpoint of Parent1 and Parent2 ? ? = 1 2 (?1 + ?2) ? ? ? Find difference vector of these parents d = ?2 ? ?1 d ? Next, find the distance between the third and forth parent and the line connecting ?1 and ?2 by use the following equation D = ?3 ? ?1 1 ? ?3 ? ?1 ? ?2 ? ?1 ?3 ? ?1 ?2 ? ?1 D ? The childs? ? is yielded by the equation ? ? = ? ? + ?? + ?=1 ??1 ?? ?? ?
- 11. New Multi-parent Crossover Operator ? The disadvantage of the UNDX is very hard to find the optimal solution close to the boundary and low diversity ? The advantage of the UNDX is good convergence rate ? Maintenance of diversity by the UNDX result is required ? Definition of proper discover area can maintain high diversity 11
- 12. Algorithm of the New Multi-parent Crossover ? Find the midpoint of Parent1 and Parent2 ? ?1 = 1 2 (?1 + ?2) ? Find the midpoint of Parent3 and Parent4 ? ?2 = 1 2 (?3 + ?4) 12 ? Find difference vector of these parents ?1 = ?2 ? ?1 ?2 = ?4 ? ?3 ? Next, find the distance between the third and forth parent and the line connecting ?1and ?2by use the following equation ?1 = ?3 ? ?1 1 ? ?3 ? ?1 ? ?2 ? ?1 ?3 ? ?1 ?2 ? ?1 ?2 = |?4 ? ?1| (1 ? ( ?4 ? ?1 ?(?2 ? ?1) ?4 ? ?1 |?2 ? ?1| )) ? Then, find the distance between the first and second parent and the line connecting ?3and ?4by use the following equation ?3 = ?1 ? ?3 1 ? ?1 ? ?3 ? ?4 ? ?3 ?1 ? ?3 ?4 ? ?3 ?4 = |?2 ? ?3| (1 ? ( ?2 ? ?3 ?(?4 ? ?3) ?2 ? ?3 |?4 ? ?3| )) ? The childs? ?1 and ? ?2 are yielded by the equation ? ?1 = ? ?1 + ?? + ?=1 ??1 ?? ?? ? ? ?2 = ? ?1 + ?? + ?=1 ??1 ?? ?? ? ? The childs? ?3 and ? ?4 are yielded by the equation ? ?3 = ? ?2 + ?? + ?=1 ??1 ?? ?? ? ? ?4 = ? ?2 + ?? + ?=1 ??1 ?? ?? ? ? Select Parent1 (?1), Parent2 (?2), Parent3 (?3) and Parent4 (?4) ?1 ?3 ?2 ?4 ? ?1 ? ?2 ?1 ?2 ?1 ?3 ?4 ? ?3 ? ?4 ? ?2 ? ?1
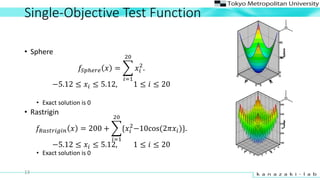
- 13. Single-Objective Test Function ? Sphere ??????? ? = ?=1 20 ?? 2 . ?5.12 ?? 5.12, 1 ? 20 ? Exact solution is 0 ? Rastrigin ?????????? ? = 200 + ?=1 20 {?? 2 ?10cos(2???)}. ?5.12 ?? 5.12, 1 ? 20 ? Exact solution is 0 13
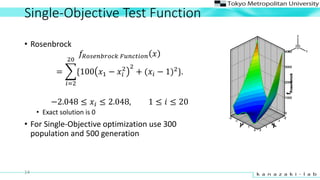
- 14. Single-Objective Test Function ? Rosenbrock ??????????? ???????? ? = ?=2 20 {100 ?1 ? ?? 2 2 + (?? ? 1)2 }. ?2.048 ?? 2.048, 1 ? 20 ? Exact solution is 0 ? For Single-Objective optimization use 300 population and 500 generation 14
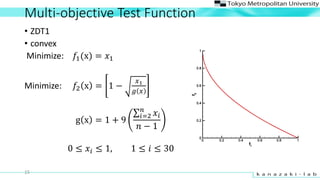
- 15. Multi-objective Test Function ? ZDT1 ? convex Minimize: ?1(x) = ?1 Minimize: ?2 x = 1 ? ?1 ? ? g x = 1 + 9 ?=2 ? ?? ? ? 1 0 ?? 1, 1 ? 30 15
- 16. Multi-objective Test Function ? ZDT2 ? Non-convex Minimize: ?1(x) = ?1 Minimize: ?2(x) = 1 ? ?1 ?(?) 2 g x = 1 + 9 ?=2 ? ?? ? ? 1 0 ?? 1, 1 ? 30 16 ? For Multi-Objective optimization use 300 population and 200 generation
- 17. Airfoil Optimization Problem ? Created airfoil my NACA 4 digit equation ? Maximum: Cl ? Minimize: Cd ? Subject to: ? 0.05 y1 0.13; the thickness in upper side of airfoil (dv1) ? 0.05 y2 0.13; the thickness in lower side of airfoil (dv2) ? 0 y3 0.04; the maximum camber of airfoil (dv3) ? 0.2 y4 0.6; the location of the maximum camber (dv4) ? Subject to: ? 0.6 cl 1.8 (dv5) ? Use 100 population and 70 generation ? Use Reynolds Number 106 17
- 18. NACA 4 digit Airfoil ? Equation for a symmetrical 4-digit NACA airfoil ?? = ? 0.2 ? 0.2969 ? ? ? 0.1260 ? ? ? 0.3516 ? ? 2 + 0.2843 ? ? 3 ? 0.1015 ? ? 4 ? Equation for a cambered 4-digit NACA airfoil ? ?? = ? ? ?2 2? ? ? ? , 0 ? ?? ? ??? (1??)2 1 + ? ? ? 2? , ?? ? ? ? The example of airfoil when use t=0.12, m=0.04 and p=0.4 18 -0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 0 0.2 0.4 0.6 0.8 1 1.2
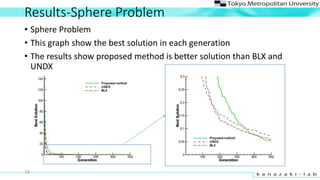
- 19. Results-Sphere Problem ? Sphere Problem ? This graph show the best solution in each generation ? The results show proposed method is better solution than BLX and UNDX 19
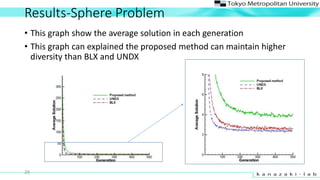
- 20. Results-Sphere Problem ? This graph show the average solution in each generation ? This graph can explained the proposed method can maintain higher diversity than BLX and UNDX 20
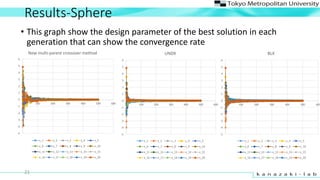
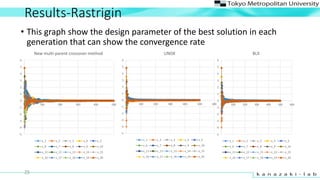
- 21. Results-Sphere 21 ? This graph show the design parameter of the best solution in each generation that can show the convergence rate -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 100 200 300 400 500 600 New multi-parent crossover method x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 100 200 300 400 500 600 UNDX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 100 200 300 400 500 600 BLX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20
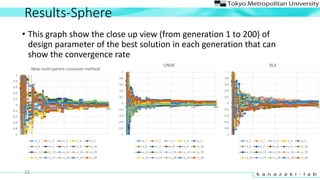
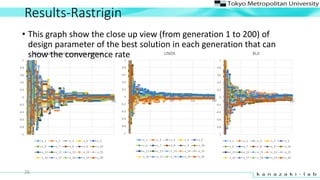
- 22. Results-Sphere 22 ? This graph show the close up view (from generation 1 to 200) of design parameter of the best solution in each generation that can show the convergence rate -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 New multi-parent crossover method x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 UNDX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 BLX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20
- 23. Results-Rastrigin Problem ? Rastrigin Problem ? This graph show the best solution in each generation ? The results show proposed method is better solution than BLX and UNDX 23
- 24. Results-Rastrigin Problem ? This graph show the average solution in each generation ? This graph can explained the proposed method can maintain higher diversity than BLX and UNDX 24
- 25. Results-Rastrigin 25 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 100 200 300 400 500 New multi-parent crossover method x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 100 200 300 400 500 600 UNDX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 100 200 300 400 500 600 BLX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 ? This graph show the design parameter of the best solution in each generation that can show the convergence rate
- 26. Results-Rastrigin 26 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 New multi-parent crossover method x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 UNDX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 BLX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 ? This graph show the close up view (from generation 1 to 200) of design parameter of the best solution in each generation that can show the convergence rate
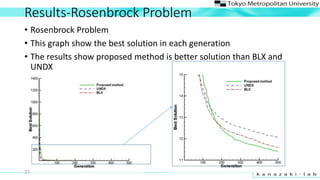
- 27. Results-Rosenbrock Problem ? Rosenbrock Problem ? This graph show the best solution in each generation ? The results show proposed method is better solution than BLX and UNDX 27
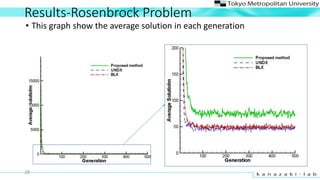
- 28. Results-Rosenbrock Problem ? This graph show the average solution in each generation 28
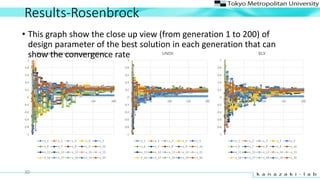
- 29. Results-Rosenbrock 29 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 100 200 300 400 500 600 New multi-parent crossover method x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 100 200 300 400 500 600 UNDX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 0 100 200 300 400 500 600 BLX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 ? This graph show the design parameter of the best solution in each generation that can show the convergence rate
- 30. Results-Rosenbrock 30 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 New multi-parent crossover method x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 UNDX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 0 50 100 150 200 BLX x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_10 x_11 x_12 x_13 x_14 x_15 x_16 x_17 x_18 x_19 x_20 ? This graph show the close up view (from generation 1 to 200) of design parameter of the best solution in each generation that can show the convergence rate
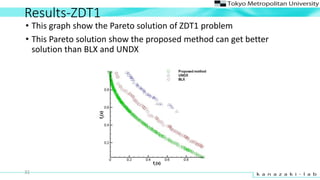
- 31. Results-ZDT1 ? This graph show the Pareto solution of ZDT1 problem ? This Pareto solution show the proposed method can get better solution than BLX and UNDX 31
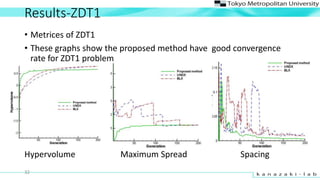
- 32. Results-ZDT1 ? Metrices of ZDT1 ? These graphs show the proposed method have good convergence rate for ZDT1 problem 32 Hypervolume Maximum Spread Spacing
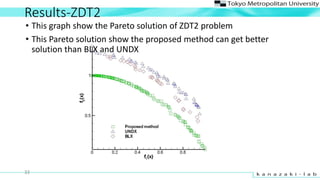
- 33. Results-ZDT2 ? This graph show the Pareto solution of ZDT2 problem ? This Pareto solution show the proposed method can get better solution than BLX and UNDX 33
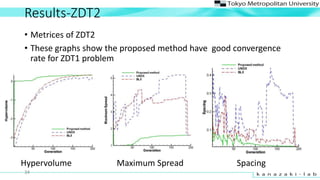
- 34. Results-ZDT2 ? Metrices of ZDT2 ? These graphs show the proposed method have good convergence rate for ZDT1 problem 34 Hypervolume Maximum Spread Spacing
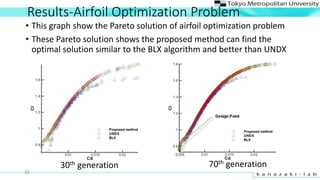
- 35. Results-Airfoil Optimization Problem ? This graph show the Pareto solution of airfoil optimization problem ? These Pareto solution shows the proposed method can find the optimal solution similar to the BLX algorithm and better than UNDX 35 30th generation 70th generation
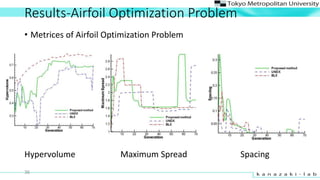
- 36. Results-Airfoil Optimization Problem ? Metrices of Airfoil Optimization Problem 36 Hypervolume Maximum Spread Spacing
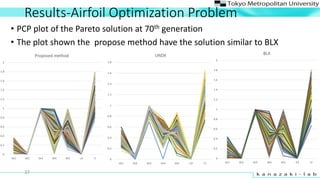
- 37. Results-Airfoil Optimization Problem 37 ? PCP plot of the Pareto solution at 70th generation ? The plot shown the propose method have the solution similar to BLX 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 dv1 dv2 dv3 dv4 dv5 Cd Cl BLX 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 dv1 dv2 dv3 dv4 dv5 Cd Cl UNDX 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 dv1 dv2 dv3 dv4 dv5 cd cl Proposed method
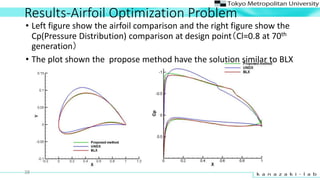
- 38. Results-Airfoil Optimization Problem ? Left figure show the airfoil comparison and the right figure show the Cp(Pressure Distribution) comparison at design pointCl=0.8 at 70th generation ? The plot shown the propose method have the solution similar to BLX 38
- 39. Conclusion ? Successful to development of new multi-parent crossover method ? The proposed method successfully find out the better solution of every test function compared with existent crossover method ? The multi-objective test function are better compared with other crossover method ? For the airfoil optimization problem the searching areas are similar because the parameterizations is relatively smile so the investigation by more complex problem is need ? This method can maintain higher diversity 39