狠狠撸

Rによるやさしい統計学

第6章
2つの平均値を比較する
#TokyoR 28th
2013/01/26
@horihorio

自己紹介
? Twitter ID:
@horihorio
? お仕事：
データマイニング?コンサルタント
（金融の分析で6年程）
? 興味事項：
統計/機械学習/DB/R/Finance/金融業/会計
? 過去の発表内容：
ここ：http://www.slideshare.net/horihorio
2013/01/26 2つの平均値を比較する 1 / 26

第6章のゴール
違いが分かる人になる。
【例題】センター英語で、現役vs浪人で差はあるか？

謎の手法 (?)でデータを入手（入手方法はあとで）
現役(N= 411734)：
153, 115, 109, 100, 35, 154, 71, 91, 52, 122, …
浪人(N= 102933) ：
163, 123, 162, 139, 40, 184, 121, 61, 90, 193, …

2013/01/26 2つの平均値を比較する 2 / 26

◇ お話内容◇
1. 【第5章の復習】
仮説検定の発想

2. 検定統計量のイメージ

3. 2つの平均値を比較する

2013/01/26 2つの平均値を比較する 3 / 26

1. 仮説検定の発想
統計的仮説検定の一般的な手順(P.111)
手順やること
1 母集団に関する帰無仮説と対立仮説（両側or片
側検定）を設定する
2 検定統計量を選ぶ
3 有意水準αの値を決める
4 （データを収集した後）データから検定統計量の実
現値を求める
5 検定統計量の実現値が棄却域に入れば帰無仮
説を棄却して、対立仮説を採択する。棄却域に入
らなければ、帰無仮説を採択する
2013/01/26 2つの平均値を比較する 4 / 26

例：以下の成果を仮説検定したい

2013/01/26 2つの平均値を比較する 5 / 26

いったん、例えば
帰無仮説
否定したいこと：

あ（今の体重）－（1年前の体重）＞0

を考え、

否定したいことの発生確率が高い/低い
で評価する。
2013/01/26 2つの平均値を比較する 6 / 26

平均5, 分散2の
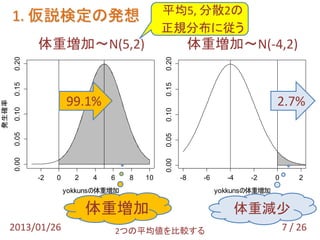
正規分布に従う
体重増加～N(5,2) 体重増加～N(-4,2)
0.20

0.20
0.15

0.15
99.1% 2.7%
発生確率

発生確率
0.10

0.10
0.05

0.05
0.00

0.00
-2 0 2 4 6 8 10 -8 -6 -4 -2 0 2
yokkunsの体重増加 yokkunsの体重増加

体重増加体重減少
2013/01/26 2つの平均値を比較する 7 / 26

◇ お話内容◇



2013/01/26 2つの平均値を比較する 8 / 26

（P.4の手順2）検定統計量って難しそう…
P143：独立な2群のt検定統計量

あ
が、自由度のt分布に従う

検定統計量のイメージを知ってほしい
（ゴマカシ有だけど…）
2013/01/26 2つの平均値を比較する 9 / 26

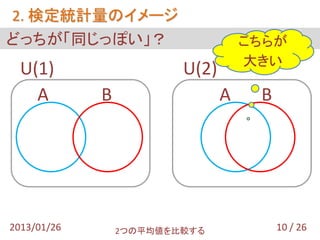
どっちが「同じっぽい」？こちらが
大きい
U(1) U(2)
A B A B

2013/01/26 2つの平均値を比較する 10 / 26

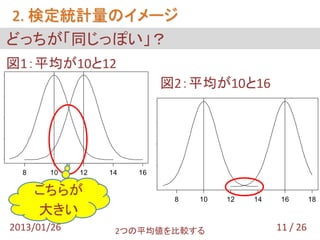
どっちが「同じっぽい」？
図1：平均が10と12
図2：平均が10と16

0.4
0.3
0.2
0.1

8 10 12 14 16
0.0

こちらが 8 10 12 14 16 18
大きい
2013/01/26 2つの平均値を比較する 11 / 26

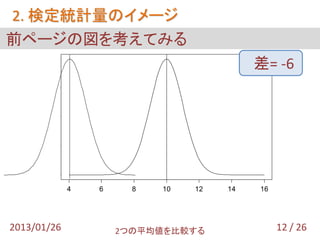
前ページの図を考えてみる
0.4

差= -6
0.3
0.2
0.1
0.0

4 6 8 10 12 14 16

2013/01/26 2つの平均値を比較する 12 / 26

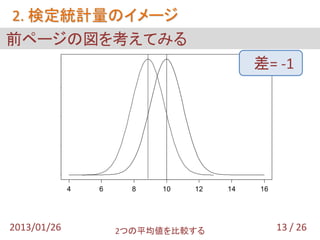
0.4

差= -1
0.3
0.2
0.1
0.0

4 6 8 10 12 14 16

2013/01/26 2つの平均値を比較する 13 / 26

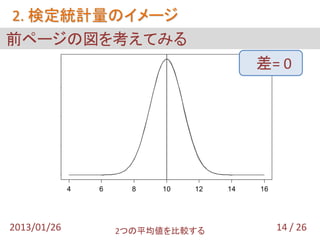
0.4

差= 0
0.3
0.2
0.1
0.0

4 6 8 10 12 14 16

2013/01/26 2つの平均値を比較する 14 / 26

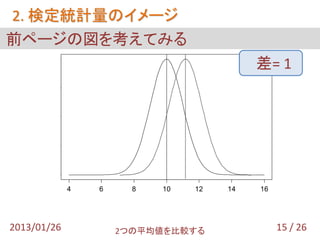
0.4

差= 1
0.3
0.2
0.1
0.0

4 6 8 10 12 14 16

2013/01/26 2つの平均値を比較する 15 / 26

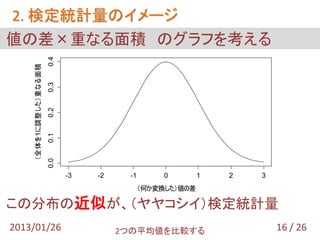
値の差×重なる面積のグラフを考える
0.4
（全体を1に調整した）重なる面積
0.3
0.2
0.1
0.0

-3 -2 -1 0 1 2 3
（何か変換した）値の差

この分布の近似が、（ヤヤコシイ）検定統計量
2013/01/26 2つの平均値を比較する 16 / 26

検定統計量は近似だよ！
? 検定統計量は、近似の前提が違うと
「INPUT：データ / OUTPUT：確率」にならない
P.148 表6.1 t検定の前提条件
1 標本抽出が無作為に行われていること（無作為抽出）
2 母集団の分布が正規分布にしたがっていること
（正規性）
3 2つの母集団の分散が等質であること
（分散の等質性）

2013/01/26 2つの平均値を比較する 17 / 26

◇ お話内容◇



2013/01/26 2つの平均値を比較する 18 / 26

2つの比較の前に：P.17の前提3つをチェック！
? 前提3：分散の等質性大抵こっちに
なる？
分散は同じ？ [異なる]
Welchの検定

[等しい]
t検定
2013/01/26 2つの平均値を比較する 19 / 26

2つの比較の前に：P.17の前提3つをチェック！
? 前提2：正規性
データが多いなら、正規分布とみなす
【参考】母集団と標本
（Tokyo.R #25 @dichika さん資料）

? 前提1：無作為抽出
? 大切だけど、ここでは省略
? 統計学に加え、分析設定のおはなし
2013/01/26 2つの平均値を比較する 20 / 26

【謎のデータ分析】手順1. 等分散チェック
> ls()
[1] "geneki" "ronin" 等分散の確率
>
?小さいので異分散
> var.test(geneki, ronin)
F test to compare two variances
data: geneki and ronin
F = 1.2459, num df = 411733,
denom df = 102932, p-value < 2.2e-16
alternative hypothesis:
true ratio of variances is not equal to 1

95 percent confidence interval:
1.235178 1.256706
sample estimates: ratio of variances 1.245919
2013/01/26 2つの平均値を比較する 21 / 26

【謎のデータ分析】手順2. Welchの検定
> t.test(geneki,ronin, var.equal=FALSE)
Welch Two Sample t-test
t = -197.3022, df = 172848.2, p-value < 2.2e-16
差=0の確率は小さい
alternative hypothesis: ?差≠0 平均値が異なる！
true difference in means is not equal to 0

95 percent confidence interval: -23.64578 -23.18061
sample estimates:
mean of x mean of y
120.8260 144.2392
2013/01/26 2つの平均値を比較する 22 / 26

【ご参考】等分散の場合の検定
> t.test(geneki, ronin, var.equal=TRUE)
Two Sample t-test
t = -184.739, df = 514665, p-value < 2.2e-16

alternative hypothesis:
true difference in means is not equal to 0

95 percent confidence interval: -23.66159 -23.16480
sample estimates:
mean of x mean of y
120.8260 144.2392

2013/01/26 2つの平均値を比較する 23 / 26

【補足】対応のあるt検定
? 対応のあるデータって？
母集団を、何かを施術/未施術で分割したペア
例：怒涛の英語力が身につく学校に
行った/行かなかった場合の比較

? この場合は、検定統計量が異なる
? Rでは、t.test(x, y, paired=TRUE) とする
? Rでの実例は、P.150～156を参照

2013/01/26 2つの平均値を比較する 24 / 26

で、データの入手源 → 下記コードだったり…
set.seed(666) # 同一乱数生成数値参考源：
# 初期乱数付与 ? 昨年のセンター試験
geneki <- rnorm(n=519867*.792, mean=123.3, sd=40) ? ベネッセ?駿台の
ronin <- rnorm(n=519867*.198, mean=152.2, sd=30) 自己採点集計
# 全数値が0～200になるまで乱数で置換
while( length(which(geneki<0|geneki>200)) ) {
geneki <- replace(geneki, which(geneki<0|geneki>200)
, rnorm(length(which(geneki<0 | geneki>200)), mean=123.3, sd=40)) }
while( length(which(ronin<0|ronin>200)) ) {
ronin <- replace(ronin, which(ronin<0|ronin>200)
, rnorm(length(which(ronin<0 | ronin>200)), mean=50, sd=60)) }
実は：両母集団とも
# 整数置換
geneki <- round(geneki); ronin <- round(ronin) 正規分布でない…
2013/01/26 2つの平均値を比較する 25 / 26

まとめ
? Welch検定/t検定：
2つの母集団に差がある？を知りたい
? 検定で重要なこと：
検定統計量の仮定に当てはまる？
? Rのコマンド：
1. 等分散か？： var.test
2. 差がある？：
t.test(x, y, var.equal=FALSE / TRUE)

2013/01/26 2つの平均値を比較する 26 / 26

狠狠撸

第6章 2つの平均値を比較する - TokyoR #28

More Related Content

第6章 2つの平均値を比較する - TokyoR #28