狠狠撸

?日付：2015/06/04
発表者：@_kobacky
場所：株式会社 ALBERT セミナールーム
トピックモデルによる統計的潜在意味解析
読書会 2章「Latent Dirichlet Allocation」
(前半)
【注意】
この資料料は ?@_kobacky が本を読んで理理解した内容を記載したものであり、
本には存在しない記述や本とは異異なる表現をしている部分があります。
【Amazon】
http://www.amazon.co.jp/dp/4339027588/

2章「Latent Dirichlet Allocation」
２.1：概要
２.2：多項分布と ?Dirichlet 分布
２.3：LDA の?生成過程

2.1 概要
?? LDA : ?文書の確率率率的?生成モデル
?? Bag of Words (BoW)
?? ?文書を単語と出現頻度度のペアの集合として表現
?? 単語の順序は無視
?? 各?文書には潜在トピックがあると仮定
?? 統計的に共起しやすい単語集合が?生成される要因を潜在トピック
という観測できない確率率率変数を?用いて定式化
?? LDA では?一つの?文書には複数の潜在トピックが存在すると仮定
?? 潜在トピックモデル
?? LDAの改良良モデルの総称
?? 共起情報が?大量量にあるようなデータ全般に適?用可能
?? Bag of Items (ユーザーの購買履履歴)や、その他 Bag of XXX

2.2 多項分布とDirichlet分布
?? LDA の説明の準備として、サイコロのイメージを?用いて
多項分布と ?Dirichlet 分布について説明
?? 多項分布
?? 各?目が出る確率率率が ?π で表されるサイコロを ?n ?回振った時に各?目が
出る回数の分布
?? Dirichlet 分布
?? サイコロの形状(出る?目の種類 K と出やすさ ?π ) ?の分布
π = π1,π2,????,πK( )
「1」が出る確率率率出る?目の種類数
サイコロの形状
(Dirichlet 分布により?生成)
πk
k=1
K
∑ =1
"
#
$
%
&
'

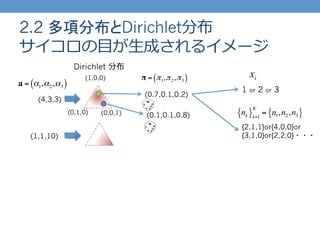
サイコロの?目が?生成されるイメージ
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
a = α1,α2,α3( )
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)

サイコロの?目が?生成されるイメージ①
a = α1,α2,α3( )
(4,3,3)
(1,1,10)
(K=3)

サイコロの?目が?生成されるイメージ②
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
a = α1,α2,α3( )
(4,3,3)
(1,1,10)
単体(simplex)：
座標の総和が1で定義される空間図
形。3次元の場合は三?角形。
※αの値と ?Dirichlet 分布
の図の対応はイメージです。

サイコロの?目が?生成されるイメージ③
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
濃い部分の点が選択されやすい

サイコロの?目が?生成されるイメージ④
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
1 or 2 or 3
xi
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
1回振って
出る?目

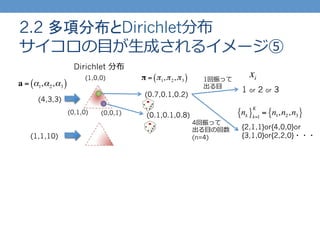
サイコロの?目が?生成されるイメージ⑤
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
a = α1,α2,α3( )
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
1回振って
出る?目
4回振って
出る?目の回数
(n=4)

サイコロの?目が?生成されるイメージ⑥
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
?? π (ベクトル)：サイコロの?目の出やすさ
?? αで特徴付けられる ?Dirichlet 分布に従う
?? xi ：1回の試?行行で出る?目
?? π の分布に従う (n=1 の多項分布に従う)
?? {nk} (集合)：各?目が出る回数
?? π と n で特徴付けられる多項分布に従う
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
1回振って
出る?目
4回振って
出る?目の回数
(n=4)
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???

式(2.1)：x ?の?生起確率率率
p x π( )= p xi π( )
i=1
n
∏ = πk
nk
k=1
K
∏
p 1,2,1,3( ) π( )= 0.7×0.1×0.7×0.2 = 0.72
×0.11
×0.21
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
【例例】x=(1,2,1,3)の場合
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
x = x1, x2, x3,???, xn( ) の?生起確率率率
式(2.1)
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???

式(2.2)：多項分布による出?目回数の?生成
p nk{ }k=1
K
π,n( )= Multi nk{ }k=1
K
π,n( )≡
n!
nk !
k=1
K
∏
πk
nk
k=1
K
∏
p 2,1,1{ } π,4( )=4 C2 ×2 C1 ×1 C1 × 0.72
×0.11
×0.21
( )=
4!
2!×1!×1!
0.72
×0.11
×0.21
( )
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10) Multi nk{ }k=1
K
π,n( )
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
式(2.2)
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???
【例例】π=(0.7,0.1,0.2)のサイコロで「1が2回、2が1回、3が1回」の場合

式(2.3)：xi ?の?生成
xi Multi xi π( )
p xi = k π( )= Multi nk =1 π,1( )=
1
nk !
k=1
K
∏
πk
nk
k=1
K
∏ = πk
p xi π( )= Multi xi π( )
?～
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
Multi xi π( )
kの?目が出た回数は1
k以外の?目が出た回数は0
であるため
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
式(2.3)
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???

式(2.4)?～式(2.6)：Dirichlet ?分布
Dirichlet 分布
(1,0,0)
(0,1,0) (0,0,1)
a = α1,α2,α3( )
π = π1,π2,π3( )
(0.7,0.1,0.2)
(0.1,0.1,0.8)
(4,3,3)
(1,1,10)
p π a( )= Dir π a( )≡
Γ αkk=1
K
∑( )
Γ αk( )k=1
K
∏
πk
αk ?1
k=1
K
∏
Γ 1( )=1
Γ n( )= n ?1( )Γ n ?1( )
Γ α + n( )= α + n ?1( )Γ α + n ?1( )
E πk[ ]=
αk
α0
V πk[ ]=
αk α0 ?αk( )
α0
2
1+α0( )
α0 = αk
k=1
K
∑
式(2.5)：ガンマ関数
式(2.6)：期待値?分散
式(2.4)：Dirichlet 分布
正規化項
(α が定まった元では定数)
1 or 2 or 3
xi
nk{ }k=1
K
= n1,n2,n3{ }
{2,1,1}or{4,0,0}or
{3,1,0}or{2,2,0}???

共役事前分布
p(x)をp(y|x)の事前分布とする。
事後分布p(x|y)∝p(y|x)p(x)の分布がp(x)と同じ分布にな
るとき、p(x)はp(y|x)の共役事前分布であるという。
xi Multi xi π( )?～
p π a( )= Dir π a( )≡
Γ αkk=1
K
∑( )
Γ αk( )k=1
K
∏
πk
αk ?1
k=1
K
∏
p π x,a( )=
Γ nk +αkk=1
K
∑( )
Γ nk +αk( )k=1
K
∏
πk
nk +αk ?1
k=1
K
∏
x の?生成過程
π の事前分布
π の事後分布
を考える。
x が観測された後の π の分布
x が観測される前の π の分布
式(2.9)
式(2.4)
事前分布?
事後分布が共に
Dirichlet 分布
αk は k の仮想的
頻度度の意?見見を持
つと?見見れる。
※導出は後ほど??

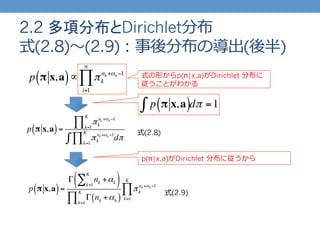
式(2.7)：事後分布の導出(前半)
p π x,a( )=
p x,π a( )
p x a( )
∝ p x,π a( )= p x π( )p π a( )
= p xi π( )p π a( )
i=1
n
∏ = πk
δ xi=k( )
k=1
K
∏ p π a( )
i=1
n
∏
= πk
δ xi=k( )i=1
n
∑
p π a( )
i=1
n
∏ = πk
nk
p π a( )
i=1
n
∏
∝ πk
nk
i=1
n
∏ πk
αk ?1
i=1
n
∏ = πk
nk +αk ?1
i=1
n
∏
P(π|a) の正則化項が定数である事に注?目
P(x|a) が定数である事に注?目

式(2.8)?～(2.9)：事後分布の導出(後半)
p π x,a( )∝ πk
nk +αk ?1
i=1
n
∏
p π x,a( )=
πk
nk +αk ?1
k=1
K
∏
πk
nk +αk ?1
dπ
k=1
K
∏∫
p π x,a( )∫ dπ =1
式の形からp(π|x,a)がDirichlet 分布に
従うことがわかる
p π x,a( )=
Γ nk +αkk=1
K
∑( )
Γ nk +αk( )k=1
K
∏
πk
nk +αk ?1
k=1
K
∏
p(π|x,a)がDirichlet 分布に従うから
式(2.8)
式(2.9)

式(2.10)
Ep π x,a( )
πk[ ]= πk p π x,a( )dπ∫ =
nk +αk
n "k +α "k"k =1
K
∑
事後分布の期待値
式(2.6) より
学習アルゴリズムの導出時に必要な計算
(おそらく後で使われる)

?? 詳細は教科書 p.30 参照
?? 要素の値が?小さいと単体の縁周辺の密度度が?高くなる。
?? 要素の値が?大きいと単体の中央周辺の密度度が?高くなる。
?? 要素間の値に差がある場合、値の?大きい要素と k が対応する ?π の
要素値が?高い領領域の密度度が?高くなる。
?? Dirichlet 分布によって単語の分布の偏りを表現できる。
α の値による ?Dirichlet 分布の変化

?? ?文書集合の解析では単語の出現分布を分析
?? ?文書集合の背景に存在するトピックを仮定
?? トピック毎に単語の出現頻度度が異異なると仮定
?? ?文書集合にはトピックの情報は明?示的に与えられていない
?? 観測できない潜在トピック(潜在変数)として抽出できるようモデル化
2.3 LDAの?生成過程
φk,v
φk = φk,1,???,φk,V( )
v = 1,2,3,???,V{ }
：トピックk における単語 v の出現確率率率
：単語のインデックス集合
：トピック k における単語の出現分布
zd,i ∈ 1,2,3,???,K{ }
wd,i ：?文書 d の ?i 番?目の単語
：?　?　に対応する潜在変数wd,i

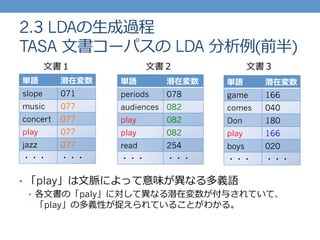
TASA ??文書コーパスの LDA 分析例例(前半)
単語潜在変数
slope 071
music 077
concert 077
play 077
jazz 077
??? ???
単語潜在変数
periods 078
audiences 082
play 082
play 082
read 254
??? ???
単語潜在変数
game 166
comes 040
Don 180
play 166
boys 020
??? ???
?文書１ ?文書２ ?文書３
?? 「play」は?文脈によって意味が異異なる多義語
?? 各?文書の「paly」に対して異異なる潜在変数が付与されていて、
「play」の多義性が捉えられていることがわかる。

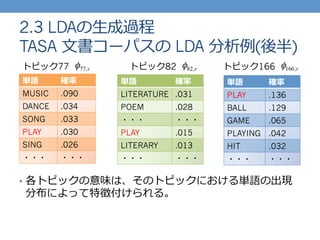
TASA ??文書コーパスの LDA 分析例例(後半)
単語確率率率
MUSIC .090
DANCE .034
SONG .033
PLAY .030
SING .026
??? ???
単語確率率率
LITERATURE .031
POEM .028
??? ???
PLAY .015
LITERARY .013
??? ???
単語確率率率
PLAY .136
BALL .129
GAME .065
PLAYING .042
HIT .032
??? ???
?? 各トピックの意味は、そのトピックにおける単語の出現
分布によって特徴付けられる。
トピック77 φ77,v トピック82 φ82,v トピック166 φ166,v

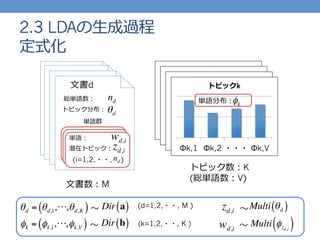
定式化
?文書d
nd総単語数：
θd
トピック分布：
?文書数：M
Φk,1 Φk,2 ??? Φk,V
トピックk
Φk,1 Φk,2 ??? Φk,V
トピックk
Φk,1 Φk,2 ??? Φk,V
トピックk
Φk,1 Φk,2 ??? Φk,V
トピックk
トピック数：K
(総単語数：V)
θd = θd,1,???,θd,K( ) (d=1,2,??, M )
(k=1,2,??, K )
?～ Dir a( )
φk = φk,1,???,φk,V( ) ?～ Dir b( )
φk単語分布：
Multi θd( )
Multi φzd,i( )wd,i
?～
?～
zd,i
単語群
(i=1,2,??, )
単語：
zd,i潜在トピック：
wd,i
nd

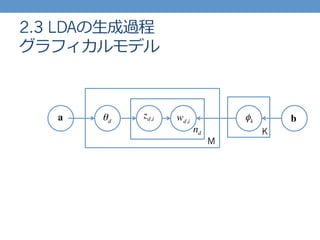
グラフィカルモデル
M
Knd
a bθd φkwd,i
zd,i

ありがとうございました！

狠狠撸

「トピックモデルによる統計的潜在意味解析」読書会 2章前半

More Related Content

「トピックモデルによる統計的潜在意味解析」読書会 2章前半