Topic models
- 1. Jeonghun Yoon Probabilistic Topic Models
- 2. Natural Language Processing Natural language(ìì°ì´) : ì¼ì ìíìì ì¬ì©íë ì¸ì´ Natural language processing(ìì°ì´ ì²ë¦¬) : ìì°ì´ì ì미를 ë¶ìíì¬ ì»´í¨í°ê° ì¬ë¬ê°ì§ ì¼ë¤ì(tasks) ì² ë¦¬í ì ìëë¡ íë ê² Easy ï¬ Spell checking, Keyword search, Finding synonyms Medium ï¬ Parsing information from websites, documents, etc Hard ï¬ Machine translation ï¬ Semantic analysis ï¬ Coherence ï¬ Question answering CS 224D : Deep Learning for NLP
- 3. Semantic analysis ì¸ì´íììì ì미 ë¶ì ï¬ ìì°ì´ë¥¼ ì´í´íë ê¸°ë² ì¤ íëë¡, 문ì¥ì ì미(meaning, semantic)ì 근거íì¬ ë¬¸ì¥ì í´ìíë ê²ì ì미 ï¬ Syntax analysisì ë°ë(lexicon, syntax analysis) 머ì ë¬ëììì ì미 ë¶ì ï¬ Corpusì ìë ë§ì documents ì§í©ì ë´ì ëì´ ìë(latent) meanings, concepts, subjects, topics ë±ì ì¶ì í ì ìë 구조를 ìì±íë ê²ì ì미 ï¬ ëíì ì¸ ì미 ë¶ì ê¸°ë² ï¬ Latent Semantic Analysis(LSA or LSI) ï¬ PLSI ï¬ Latent Dirichlet Allocation(LDA) ï¬ Hieararchical Dirichlet Processing(HDP)
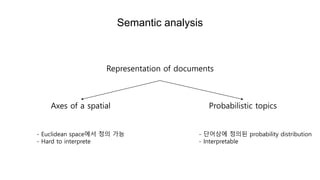
- 4. Semantic analysis Representation of documents Axes of a spatial Probabilistic topics - Euclidean spaceìì ì ì ê°ë¥ - Hard to interprete - ë¨ì´ìì ì ìë probability distribution - Interpretable
- 5. 1. Axes of a spatial - LSA 2. Probabilistic topics - LDA 3. Bayesian Nonparametric - HDP
- 6. LSA (Latent Semantic Analysis) ï¬ LSA(LSI)ë document dataì ì¨ê²¨ì§ ì미(hidden concept)를 ì°¾ìë´ë 기ë²ì´ë¤. ï¬ LSAë ê°ê°ì 문ì(document)ì ë¨ì´(word)를 벡í°ë¡ íííë¤. 벡í°ë´ìì ê°ê°ì elementë ì¨ê²¨ì§ ìë¯¸ê° ë ê²ì´ë¤.
- 7. LSA (Latent Semantic Analysis) ï¬ 3ë² ë¬¸ìë 쿼리ì ëí´ì 1ë±ì´ ë ê²ì´ë¤. ï¬ 2ë², 4ë² ë¬¸ìë ê·¸ ë¤ìì´ ë ê²ì´ë¤. ï¬ 1ë², 5ë² ë¬¸ìë? ï¼ ì¬ëë¤ì´ ì¸ìí기ë¡ë 문ì 1ë²ì´ 문ì 5ë² ë³´ë¤ ì£¼ì´ì§ 쿼리ì ë ë§ë 문ìì´ë¤. ì»´í¨í°ë ì´ë¬í ì¶ë¡ ê³¼ì ì í ì ììê¹? ì¦ ì¨ê²¨ì§ ì미를 ì°¾ì ì ììê¹? ð1 : Romeo and Juliet. ð2 : Juliet: O happy dagger! ð3 : Romeo died by dagger. ð4 : "Live free or die", that's the motto of New-Hampshire ð5 : Did you know, New-Hampshire is in New-England ðð¢ððð¦ : dies and dagger
- 8. LSA (Latent Semantic Analysis) matrix ð¨ : romeo juliet happy dagger live die free new-hampshire ð1 ð2 ð3 ð4 ð5
- 9. LSA (Latent Semantic Analysis) matrix ð¨ : romeo juliet happy dagger live die free new-hampshire ð1 ð2 ð3 ð4 ð5
- 10. doc-doc matrix matrix ð¨ : matrix ð¨ ð»: matrix ð¨ð¨ ð»(ð©): 5 à 8 8 à 5 5 à 5 1ë² ë¬¸ììë romeo, juliet, 2ë² ë¬¸ììë juliet, happy, dagger ì¦ ê²¹ì³ì§ë ê²ì´ 1ê°ì´ë¯ë¡ ðµ 1,2 = ðµ 2,1 = 1 matrix ð© = ð´ð´ ð doc-doc matrix 문ì ðì 문ì ðê° ðê° ì ê³µíµ ë¨ì´ë¥¼ ê°ì§ê³ ìì¼ë©´ ðµ ð, ð = ð
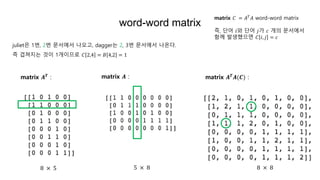
- 11. word-word matrix 8 à 5 5 à 8 8 à 8 matrix ð¨ :matrix ð¨ ð» : matrix ð¨ ð» ð¨(ðª) : julietì 1ë², 2ë² ë¬¸ììì ëì¤ê³ , daggerë 2, 3ë² ë¬¸ììì ëì¨ë¤. ì¦ ê²¹ì³ì§ë ê²ì´ 1ê°ì´ë¯ë¡ ð¶ 2,4 = ðµ 4,2 = 1 matrix ð¶ = ð´ ð ð´ word-word matrix ì¦, ë¨ì´ ðì ë¨ì´ ðê° ð ê°ì 문ììì í¨ê» ë°ìíì¼ë©´ ð¶ ð, ð = ð
- 12. LSA (Latent Semantic Analysis) SVD ì¬ì©! ð´ = ðΣð ð, ðë ðµì eigenvectorsì´ê³ , ðë ð¶ì eigenvectorsì´ë¤. singular value
- 13. LSA (Latent Semantic Analysis) Reduced SVD ì¬ì©! ð´ ð = ð ðΣk ð ð ð , 모ë singular value를 ì¬ì©í ì ìê³ , ìì ê²ë¤ì ì ì¸íë¤. ðê°ì í¹ì´ê°ë§ ë¨ê¸°ë ê²ì´ë¤. ì¦ ðê°ì "hidden concepts"ë§ ë¨ê¸´ë¤.
- 14. LSA (Latent Semantic Analysis) Σ2 ð2 ð = ð2 ð = Word vector
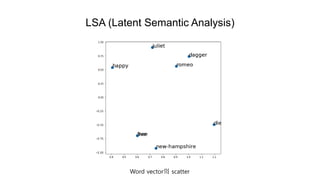
- 15. LSA (Latent Semantic Analysis) Word vectorì scatter
- 16. LSA (Latent Semantic Analysis) ð2Σ2 = ð2 = Document vector ð1 ð2 ð3 ð4 ð5 ð1 ð2 ð3 ð4 ð5
- 17. LSA (Latent Semantic Analysis) Document vectorì scatter
- 18. LSA (Latent Semantic Analysis) Word / Document vectorì scatter
- 19. LSA (Latent Semantic Analysis) cosine similarity = ð ðâð ð ð ðð = ð1 + ð2 2 query : dagger, die result :
- 20. LSA (Latent Semantic Analysis) Word / Document / Query vectorì scatter
- 21. 1. Axes of a spatial - LSA 2. Probabilistic topics - LDA 3. Bayesian Nonparametric - HDP
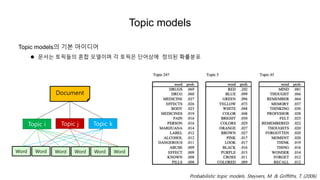
- 22. Topic models Topic modelsì 기본 ìì´ëì´ ï¬ ë¬¸ìë í í½ë¤ì í¼í© 모ë¸ì´ë©° ê° í í½ì ë¨ì´ìì ì ìë íë¥ ë¶í¬ Document Topic i Topic j Topic k Word Word Word Word Word Word Probabilistic topic models. Steyvers, M. & Griffiths, T. (2006)
- 23. Topic models - Topic A: 30% broccoli, 15% bananas, 10% breakfast, 10% munching, ⦠- Topic B: 20% cats, 20% cute, 15% dogs, 15% hamster, ⦠Doc 1 : I like to eat broccoli and bananas. Doc 2 : I ate a banana and tomato smoothie for breakfast. Doc 3 : Dogs and cats are cute. Doc 4 : My sister adopted a cats yesterday. Doc 5 : Look at this cute hamster munching on a piece of broccoli. ìì ) - Doc 1 and 2 : 100% topic A - Doc 3 and 4 : 100% topic B - Doc 5 : 60% topic A, 40% topic B
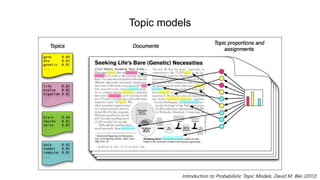
- 24. Topic models Introduction to Probabilistic Topic Models. David M. Blei (2012)
- 25. Topic models Introduction to Probabilistic Topic Models. David M. Blei (2012) (Left) 문ìììì topic proportion (Right) 문ììì ë¹ì¤ì´ ëìë í í½ì ëíì¬, í í½ë³ 문ìë´ ë¹ëìê° ê°ì¥ ëì ë¨ì´
- 26. Probabilistic Topic Modelsì 구조 모ë¸ì ì ìì ìì, íìí ë¨ì´ë¤ì ìíì í기 ï¬ Word : 1, ⦠, ð 를 ì¸ë±ì¤ë¡ ê°ì§ë vocaburary ìì items ï¬ Document : ð wordì sequence ï¬ ð¨ = ð¤1, ð¤2, ⦠, ð¤ ð , ð¤ ð : wordì sequenceë´ìì ðë²ì§¸ì ìë word ï¬ Corpus : ð· documentsì collection ï¬ ð¶ = ð¨1, ð¨2, ⦠, ð¨ ð·
- 27. Probabilistic Topic Modelsì 구조 문ì ðì ë¨ì´ ð¤ð ëí ë¶í¬ : ð ð¤ð = ð=1 ð¾ ð ð¤ð|ð§ð = ð ð ð§ð = ð ï¬ ð ð¤ð|ð§ð = ð : í í½ ðìì, ë¨ì´ ð¤ðì probability ï¬ ê° í í½ìì ì´ë¤ ë¨ì´ë¤ì´ ì¤ìí ê¹? ï¬ ð ð§ð = ð : ðë²ì§¸ ë¨ì´ì í í½ ðê° í ë¹ëë probability (ì¦, í í½ ðê° ðë²ì§¸ ë¨ì´ë¥¼ ìí´ ìíë§ ë íë¥ ) ð½ ð = ð ð¤|ð§ = ð : í í½ ðìì, ë¨ì´ë¤ì multinomial distribution ð ð = ð ð§ : 문ì ðìì, í í½ë¤ì multinomial distribution
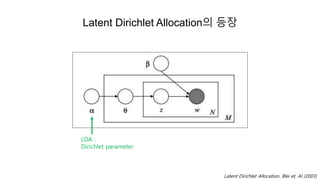
- 28. Latent Dirichlet Allocationì ë±ì¥ 문ì ðì ë¨ì´ ð¤ð ëí ë¶í¬ : ð ð¤ð = ð=1 ð¾ ð ð¤ð|ð§ð = ð ð ð§ð = ð ë리í´ë ë¶í¬(Dirichlet distribution)ì multinomial distributionì 켤ë ì¬ì ë¶í¬ë¡(conjugate prior) ì¬ì© ë¤í ë¶í¬(Multinomial distribution) ð = ð1, ⦠, ð ð¾ ì ëí Dirichlet distribution : ð·ðð ð¼1, ⦠, ð¼ ð¾ = Î ð ð¼ ð ð Î ð¼ ð ð=1 ð¾ ð ð ð¼ ðâ1 ï¬ Hyperparameter ð¼ð : 문ì ðìì í í½ ðê° ìíë§ ë íìì ëí ì¬ì ê´ì°° count (문ìë¡ë¶í° ë¨ì´ê° ì¤ì ë¡ ê´ ì°°ë기 ì´ì ì ê°) LDAë Dirichlet distributionì ðì priorë¡ ì¬ì© (Blei et. Al, 2003)
- 29. Latent Dirichlet Allocationì ë±ì¥ Latent Dirichlet Allocation. Blei et. Al (2003) LDA : Dirichlet parameter
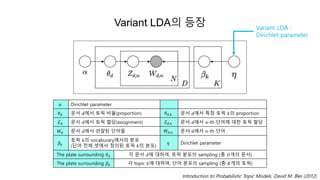
- 30. Variant LDAì ë±ì¥ 문ì ðì ë¨ì´ ð¤ð ëí ë¶í¬ : ð ð¤ð = ð=1 ð¾ ð ð¤ð|ð§ð = ð ð ð§ð = ð Hyperparameter ð : Corpusì ë¨ì´ê° ê´ì°°ë기 ì´ì ì, í í½ìì ë¨ì´ê° ìíë§ ë íìì ëí ì¬ì ê´ì°° count Varian LDAë symmetric Dirichlet distribution(ð¼)ì ð·ì priorë¡ ì¬ì© (Griffiths and Steyvers, 2004)
- 31. Variant LDAì ë±ì¥ Variant LDA : Dirichlet parameter Introduction to Probabilistic Topic Models. David M. Blei (2012) ð¼ Dirichlet parameter ð ð 문ì ðìì í í½ ë¹ì¨(proportion) ð ð,ð 문ì ðìì í¹ì í í½ ðì proportion ð ð 문ì ðìì í í½ í ë¹(assignment) ð ð,ð 문ì ðìì ð-th ë¨ì´ì ëí í í½ í ë¹ ðð 문ì ðìì ê´ì°°ë ë¨ì´ë¤ ðð,ð 문ì ðìì ð-th ë¨ì´ ð½ ð í í½ ðì vocaburaryììì ë¶í¬ (ë¨ì´ ì ì²´ ì ìì ì ìë í í½ ðì ë¶í¬) ð Dirichlet parameter The plate surrounding ð ð ê° ë¬¸ì ðì ëíì¬, í í½ ë¶í¬ì sampling (ì´ ð·ê°ì 문ì) The plate surrounding ð½ ð ê° topic ðì ëíì¬, ë¨ì´ ë¶í¬ì sampling (ì´ ð¾ê°ì í í½)
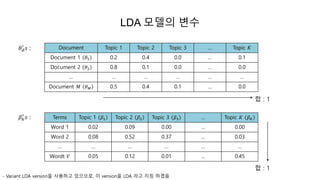
- 32. LDA 모ë¸ì ë³ì ð ð â² ð : ð½ ð â² ð : Document Topic 1 Topic 2 Topic 3 ⦠Topic ð¾ Document 1 ð1 0.2 0.4 0.0 ⦠0.1 Document 2 ð2 0.8 0.1 0.0 ⦠0.0 ⦠⦠⦠⦠⦠⦠Document ð ð ð 0.5 0.4 0.1 ⦠0.0 Terms Topic 1 ð½1 Topic 2 ð½2 Topic 3 ð½3 ⦠Topic ð¾ ð½ ð¾ Word 1 0.02 0.09 0.00 ⦠0.00 Word 2 0.08 0.52 0.37 ⦠0.03 ⦠⦠⦠⦠⦠⦠Wordt ð 0.05 0.12 0.01 ⦠0.45 í© : 1 í© : 1 - Variant LDA versionì ì¬ì©íê³ ìì¼ë¯ë¡, ì´ versionì LDA ë¼ê³ ì§ì¹ íê² ì
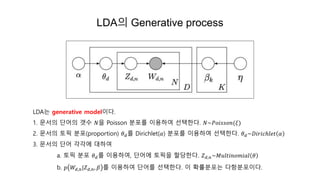
- 33. LDAì Generative process LDAë generative modelì´ë¤. 1. 문ìì ë¨ì´ì ê°¯ì ðì Poisson ë¶í¬ë¥¼ ì´ì©íì¬ ì ííë¤. ð~ðððð ð ðð(ð) 2. 문ìì í í½ ë¶í¬(proportion) ð ð를 Dirichlet(ð¼) ë¶í¬ë¥¼ ì´ì©íì¬ ì ííë¤. ð ð~ð·ððððâððð¡ ð¼ 3. 문ìì ë¨ì´ ê°ê°ì ëíì¬ a. í í½ ë¶í¬ ð ð를 ì´ì©íì¬, ë¨ì´ì í í½ì í ë¹íë¤. ð ð,ð~ðð¢ðð¡ððððððð ð b. ð ðð,ð|ð ð,ð, ð½ 를 ì´ì©íì¬ ë¨ì´ë¥¼ ì ííë¤. ì´ íë¥ ë¶í¬ë ë¤íë¶í¬ì´ë¤.
- 34. LDAì Generative process ìì ) 1. ìë¡ì´ 문ì ð·ì 길ì´ë¥¼ 5ë¡ ì ííë¤. ì¦, ð· = ð¤1, ð¤2, ð¤3, ð¤4, ð¤5 2. 문ì ð·ì í í½ ë¶í¬ë¥¼ 50%ë ìì(food), 50%ë ë물(animal)ë¡ ì ííë¤. 3. ê° ë¨ì´ì ëíì¬, 1. 첫ë²ì§¸ ë¨ì´ ð¤1ì food topicì í ë¹íë¤. Food topicìì broccoli를 ð¤1ì¼ë¡ ì ííë¤. 2. ëë²ì§¸ ë¨ì´ ð¤2ì animal topicì í ë¹íë¤. Animal topicìì panda를 ð¤2ì¼ë¡ ì ííë¤. 3. ì¸ë²ì§¸ ë¨ì´ ð¤3ì animal topicì í ë¹íë¤. Animal topicìì adorable 를 ð¤3ì¼ë¡ ì ííë¤. 4. ë¤ë²ì§¸ ë¨ì´ ð¤4ì food topicì í ë¹íë¤. Food topicìì cherries 를 ð¤4ì¼ë¡ ì ííë¤. 5. ë¤ì¯ë²ì§¸ ë¨ì´ ð¤5ì food topicì í ë¹íë¤. Food topicìì eating 를 ð¤5ì¼ë¡ ì ííë¤. ð· : broccoli panda adorable cherries eating
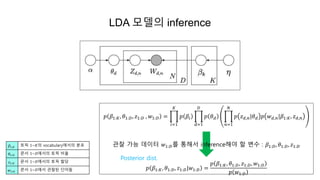
- 35. LDA 모ë¸ì inference ê´ì°° ê°ë¥í 문ì ë´ ë¨ì´ ðð,ð를 ì´ì©íì¬, LDA 모ë¸ì ì ì¬ ë³ì(hidden variable)ì¸ ë¬¸ìì í í½ë¶í¬ ð ð ì í í½ì ë¨ì´ë¶í¬ ð½ ð를 ì¶ì íë ê³¼ì ì´ inferenceì´ë¤. Generative probabilistic modelingììë, dataë ì ì¬ ë³ì(hidden variable)를 í¬í¨íë generative processììë¶í° ë°ìíëê²ì¼ë¡ ë¤ë£¬ë¤. ë°ë¼ì, generative processë observed random variableê³¼ hidden random variableì ê²°í© íë¥ ë°ë(joint probability distribution)를 ì ìíë¤. ï¬ Observed variables : 문ìë´ì ë¨ì´ë¤ ï¬ Hidden variables : 문ìì í í½ ë¶í¬, í í½ì ë¨ì´ ë¶í¬ (topic structure) ê²°í© íë¥ ë°ëí¨ì를 ì´ì©íì¬ observed variableì´ ì£¼ì´ì¡ì ë hidden variableì ì¡°ê±´ë¶ ë¶í¬ë¥¼ 구íë¤. ì´ ë¶í¬ë ì¬í íë¥ ë¶í¬(posterior distribution)ì´ë¤.
- 36. ð ð½1:ð¾, ð1:ð·, ð§1:ð· , ð¤1:ð· = ð=1 ð¾ ð ð½ð ð=1 ð· ð ð ð ð=1 ð ð ð§ ð,ð|ð ð ð ð¤ ð,ð|ð½1:ð¾, ð§ ð,ð ê´ì°° ê°ë¥ ë°ì´í° ð¤1:ð·ë¥¼ íµí´ì inferenceí´ì¼ í ë³ì : ð½1:ð·, ð1:ð·, ð§1:ð· ð ð½1:ð¾, ð1:ð·, ð§1:ð·|ð¤1:ð· = ð ð½1:ð¾, ð1:ð·, ð§1:ð·, ð¤1:ð· ð ð¤1:ð· LDA 모ë¸ì inference ð½1:ð¾ í í½ 1~ð¾ì vocabularyììì ë¶í¬ ð1:ð· 문ì 1~ð·ììì í í½ ë¹ì¨ ð§1:ð· 문ì 1~ð·ììì í í½ í ë¹ ð¤1:ð· 문ì 1~ð·ìì ê´ì°°ë ë¨ì´ë¤ Posterior dist.
- 37. LDA 모ë¸ì inference Posterior distributionì 구íë ê²ì ì¬ì´ê²ì¸ê°? ë¶ìì ê²½ì°ë¥¼ 먼ì ì´í´ë³´ì. ð ð½1:ð¾, ð1:ð·, ð§1:ð·|ð¤1:ð· = ð ð½1:ð¾, ð1:ð·, ð§1:ð·, ð¤1:ð· ð ð¤1:ð· 모ë random variableì ê²°í© íë¥ ë°ë í¨ìë, hidden variableì´ ììë¡ ì í ëë¤ë©´ ì½ê² ê³ì° ê°ë¥
- 38. LDA 모ë¸ì inference ë¶ëª¨ì ê²½ì°ë¥¼ ì´í´ë³´ì. ð ð½1:ð¾, ð1:ð·, ð§1:ð·|ð¤1:ð· = ð ð½1:ð¾, ð1:ð·, ð§1:ð·, ð¤1:ð· ð ð¤1:ð· Observed variableì ì£¼ë³ ë°ëí¨ì(marginal probability) - ììì topic modelìì, observed corpus를 ë³¼ ì ìì íë¥ ì 구íë ê² - 모ë hidden topic structureì ê°ë¥í ê²½ì°(instantiation)를 구íê³ , ê²°í© íë¥ ë°ë í¨ì를 summation ê°ë¥í hidden topic sturctureë ì§ìì ì¼ë¡ ë§ë¤. ë°ë¼ì í´ë¹ ë°ëí¨ì를 구íë ê²ì ë§¤ì° ì´ë µë¤. Modern probabilistic models, Bayesian statisticsììë ë¶ëª¨ì ë¶í¬ ë문ì posterior를 ê³ì°íë ê²ì´ ì´ë µë¤. ë°ë¼ì posterior를 í¨ê³¼ì ì¼ë¡ ì¶ì íë 기ë²ì ëí ì°êµ¬ê° ë§ì´ ì´ë£¨ì´ì§ê³ ìë¤. ë°ë¼ì, topic modeling algorithmsììë posterior distributionì ì¶ì í기 ìí 기ë²ì íì©íë¤. - sampling based method - variational method
- 39. Difficulty of deriving marginal probability ð ð¤1:ð· ï¬ Topic mixture ðì joint distribution (parameter : ð¼, ð½) ð ð, ð«, ð¨ ð¼, ð½ = ð ð|ð¼ ð=1 ð ð ð§ ð|ð ð ð¤ ð|ð§ ð, ð½ ï¬ Documentì marginal distribution ð ð¨|ð¼, ð½ = ð ð|ð¼ ð=1 ð ð§ ð ð ð§ ð|ð ð ð¤ ð|ð§ ð, ð½ ðð ï¬ Corpusì probability ð ð·|ð¼, ð½ = ð=1 ð ð ð ð|ð¼ ð=1 ð ð ð§ ðð ð ð§ ðð|ð ð ð ð¤ ðð|ð§ ðð, ð½ ðð ð ì¬ê¸°ìì notationì Latent Dirichlet Allocation. Blei et. Al (2003)ì ì°¸ê³
- 40. Algorithm for extracting topics Gibbs sampling ð· ðð = ð|ðâð, ð¤ð, ðð,â â ð¶ ð¤ ð ð ðð¾ + ð ð¤=1 ð ð¶ ð¤ð ðð¾ + ðð ð¶ ðð ð ð·ð¾ + ð¼ ð¡=1 ð¾ ð¶ ð ð ð¡ ð·ð¾ + ðð¼ 문ììì ðë²ì§¸ì ëì¤ë ë¨ì´ ð¤ì í í½ì´ ðì¼ íë¥ ì ìí¥ì 미ì¹ë ìì - ìì 1 : í í½ ðì í ë¹ë ì ì²´ ë¨ì´ ì¤ìì í´ë¹ ë¨ì´ì ì ì ì¨ì´ ëììë¡ ðì¼ íë¥ ì´ í¬ë¤. - ìì 2 : wðê° ìí 문ì ë´ ë¤ë¥¸ ë¨ì´ê° í í½ ðì ë§ì´ í ë¹ëìììë¡ ðì¼ íë¥ ì´ í¬ë¤. ð§ð = ð 문ììì ðë²ì§¸ì ëì¤ë ë¨ì´ ð¤ì í í½ ðê° í ë¹ ð«âð ðë²ì§¸ ë¨ì´ë¥¼ ì ì¸í ë¤ë¥¸ ë¨ì´ë¤ì ëí í í½ í ë¹ ð¤ð ë¨ì´ index ðð 문ì index â ë¤ë¥¸ ì ë³´ ë° observed information ð¶ ð¤ð ðð¾ ë¨ì´ ð¤ê° í í½ ðì í ë¹ë íì (íì¬ ðë ì ì¸) ð¶ ðð ð·ð¾ 문ì ðì ë¨ì´ë¤ ì¤ìì í í½ ðì í ë¹ë íì (íì¬ ðë ì ì¸) ð í í½ì ë¨ì´ ë¶í¬ ìì±ì ì¬ì©ëë Dirichlet parameter ð¼ 문ìì í í½ ë¶í¬ ìì±ì ì¬ì©ëë Dirichlet parameter Smoothing
- 41. Algorithm for extracting topics Doc 0 : ð§0,0, ð§0,1, ð§0,2, ð§0,3 Doc 1 : (ð§1,0, ð§1,1, ð§1,2) Doc 2 : (ð§2,0, ð§2,1, ð§2,2, ð§2,3) Doc 3 : (ð§3,0, ð§3,1, ð§3,2, ð§3,3, ð§5,4) Doc 4 : (ð§4,0, ð§4,1, ð§4,2, ð§4,3, ð§4,4) Doc 5 : (ð§5,0, ð§5,1, ð§5,2, ð§5,3, ð§5,4, ð§5,5) ìì ) ð§ð,ð : ðë²ì§¸ 문ìì ð í í½ì´ í ë¹ë ê²ì ëíë´ë íë¥ ë³ì 1. íë¥ ë³ìì ëë¤íê² í í½ì í ë¹ 2. ð§0,0ì ì ì¸í ê°ë¤ì í ëë¡ ð§0,0ì ê°ì ì ë°ì´í¸ 3. ð§0,1ì ì ì¸í ê°ë¤ì í ëë¡ ð§0,1ì ê°ì ì ë°ì´í¸ â¦. 4. ð§5,5ì ì ì¸í ê°ë¤ì í ëë¡ ð§5,5ì ê°ì ì ë°ì´í¸ 5. íë¥ ë³ìê° ìë ´í ëê¹ì§ ë°ë³µ
- 42. Algorithm for extracting topics ð¶ ðð¾ = ð¶11 ð¶12 ⦠ð¶21 ð¶22 ⦠⦠⦠⦠ð¶1ð ⦠ð¶1ð¾ ð¶2ð ⦠ð¶2ð¾ ⦠⦠⦠ð¶ ð£3 ð¶ ð£3 ⦠⦠⦠⦠ð¶ ð1 ð¶ ð2 ⦠ð¶ ð£ð ⦠ð¶ ð£ð¾ ⦠⦠⦠ð¶ ðð ⦠ð¶ ðð¾ ð¶ ð·ð¾ = ð¶11 ð¶12 ⦠ð¶21 ð¶22 ⦠⦠⦠⦠ð¶1ð ⦠ð¶1ð¾ ð¶2ð ⦠ð¶2ð¾ ⦠⦠⦠ð¶ ð3 ð¶ ð3 ⦠⦠⦠⦠ð¶ ð·1 ð¶ ð·2 ⦠ð¶ ðð ⦠ð¶ ðð¾ ⦠⦠⦠ð¶ ð·ð ⦠ð¶ ð·ð¾
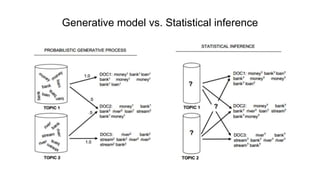
- 43. Generative model vs. Statistical inference
- 44. ìµì ì í í½ ì Perplexity ï¬ Language modelingìì ì£¼ë¡ ì»¨ë²¤ì ì¼ë¡ ì¬ì©íë¤. ï¬ ì¼ë°ì ì¼ë¡ perplexityë exp ð» ð ë¡ ííëë¤. ð» ð ë ðì ìí¸ë¡í¼ë¥¼ ì미íë¤. ï¬ LDAìì ì¶ì ë í í½ ì 보를 ì´ì©íì¬ ë¨ì´ì ë°ì íë¥ ì ê³ì°íìì ë, íë¥ ê°ì´ ëììë¡ generative process를 ì ëë¡ ì¤ëª íë¤ê³ 본ë¤. ððððððð¥ðð¡ð¦ ð¶ = exp â ð=1 ð· log ð ð¨ ð ð=1 ð· ðð ï¬ ð ð¨ ð : í í½ì ë¨ì´ë¶í¬ ì ë³´ì 문ìë´ í í½ì ë¹ì¤ ì ë³´ì ê³±ì ì´ì©íì¬ ê³ì° ï¬ ð ð¨ ð ë í´ìë¡ ì¢ì¼ë¯ë¡, perplexityë ìììë¡ ì¢ë¤.
- 45. ìµì ì í í½ ì Topic coherence ï¬ ì¤ì ë¡ ì¬ëì´ í´ìí기ì(interpretability) ì í©í íê° ì²ë를 ë§ë¤ê¸° ìí´ ì ìë ì¬ë¬ ì²ëë¤ ì¤ íë ï¬ Newmanì ë´ì¤ì ì± ë°ì´í°ë¥¼ ìì§íì¬ í í½ ëª¨ë¸ë§ì ì¤ì. ê·¸ ê²°ê³¼ë¡ ëì¨ í í½ë¤ì´ ì ì미íì§ ììì ì¼ë¡ ì ìí. ê·¸ë¦¬ê³ ì´ë ê² ë§¤ê²¨ì§ ì ìì ê°ì¥ ì ì¬í 결과를 ë¼ ì ìë ì²ë를 ì ì. ï¬ í í½ ëª¨ë¸ë§ ê²°ê³¼ë¡ ëì¨ ê°ê°ì í í½ìì ìì ðê°ì ë¨ì´ë¥¼ ì íí í, ìì ë¨ì´ ê°ì ì ì¬ë를 ê³ì°íì¬, ì¤ ì ë¡ í´ë¹ í í½ì´ ì미ì ì¼ë¡ ì¼ì¹íë ë¨ì´ë¤ë¼ë¦¬ 모ì¬ìëì§ íë¨ ê°ë¥ ï¬ ë¤ìí ë²ì ï¬ NPMI ï¬ UMass ï¬ UCI ï¬ c_v Newman, D., Lau, J. H., Grieser, K., & Baldwin, T. (2010, June). Automatic evaluation of topic coherence. In Human Language Technologies
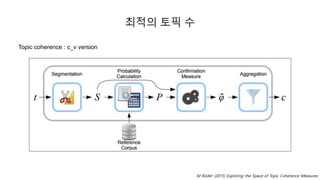
- 46. ìµì ì í í½ ì Topic coherence : c_v version M Röder (2015) Exploring the Space of Topic Coherence Measures
- 47. 1. Axes of a spatial - LSA 2. Probabilistic topics - LDA 3. Bayesian Nonparametric - HDP
- 48. Dirichlet Process LDAë í í½ì ì ðê° íìíë¤. ë°ì´í°ì ëíì¬, ì´ ë°ì´í°ì ëª ê°ì í í½ì´ ì¡´ì¬íëì§ ë¯¸ë¦¬ ìë ê²ì ì´ë µë¤. ì´ ë¶ë¶ì´ LDAì ì½ì ì¤ íëì´ë¤. íì§ë§ ì°ë¦¬ë ë°ì´í°ì ë°ë¼ ì ì í í í½ ê°ì를 ì°¾ì ì ìì¼ë©° ì´ê²ì Dirichlet Process를 ì´ì©íì¬ êµ¬í ì ìë¤. Dirichlet distributionì 주ì´ì§ íì´í¼íë¼ë¯¸í°ì ë°ë¼ ë¤íë¶í¬ë¥¼ ìì±í´ì£¼ë ë¶í¬ë¼ê³ í ì ìë¤. ë°ë¼ì ë리í´ë ë¶í¬ë¥¼ ì¬ì ë¶í¬ë¡ ëë©´, ë¤íë¶í¬ë¥¼ ë°ë¥´ë ì¬ííë¥ ë¶í¬ë¥¼ ì½ê² 구í ì ìë¤. (ë리í´ë ë¶í¬ ë ë¤íë¶í¬ì 켤ë ë¶í¬ì´ë¤.)
- 49. Dirichlet Process ðê° ë리í´ë ë¶í¬ë¥¼ ë°ë¥¸ë¤ê³ ê°ì íì. ì¦ ð~ð·ðð(1,2,1)ë¼ê³ íì. ì¬ê¸°ì ð = 3ì´ë¤. ë°ë¼ì ì´ ë¶í¬ìì í본ì ì¶ì¶íë¤ë©´ 3ê°ì ì±ë¶ì¼ë¡ë§ ì´ë£¨ì´ì§, ê·¸ë¦¬ê³ ììì í©ì´ 1ì¸ ìíë¤ì´ ìì±ë ê²ì´ë¤. ð©1 = 0.2,0.5,0.3 ð©2 = 0.1,0.6, 0.3 ⦠ë리í´ë ë¶í¬ë¥¼ ìë¡ ë¤ë¥¸ ðê°ì´ ëì¬ ì ìë ë¶í¬ë¡ íì¥ì í ê²ì´ ë¤ìì Dirichlet Processì´ë¤. ð~ð·ð ð¼, ð» ð¼ë ì§ì¤ íë¼ë¯¸í°(concentration parameter)ì´ê³ ð»ë 모ë¶í¬ì´ë¤. ð¼ê° 0ì ê°ê¹ì¸ìë¡ ðì ë¶í¬ë 모ë¶í¬ ì íê· ì ì¤ì¬ì¼ë¡ 모ì´ê³ , ð¼ê° 커ì§ìë¡ ëª¨ë¶í¬ì íê· ìì ë©ì´ì§ê² ëë¤. YW The Et al.(2005) Hierarchical Dirichlet Processes
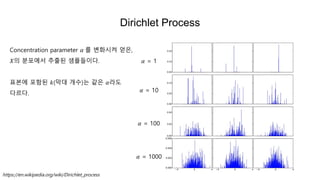
- 50. Dirichlet Process ð¼ = 1 ð¼ = 10 ð¼ = 100 ð¼ = 1000 https://en.wikipedia.org/wiki/Dirichlet_process Concentration parameter ð¼ 를 ë³íìì¼ ì»ì, ðì ë¶í¬ìì ì¶ì¶ë ìíë¤ì´ë¤. í본ì í¬í¨ë ð(ë§ë ê°ì)ë ê°ì ð¼ë¼ë ë¤ë¥´ë¤.
- 51. Chinese Restaurant Process í ì¤êµì§ì´ ìê³ , ê·¸ ì¤êµì§ìë 무ìí ë§ì ìíì´ ìë¤. ìíìë 무ìí ë§ì ìë¦¬ê° ìì´ì ìëì´ ì¼ ë§ë ì§ ìì ì ìë¤. ë¨, ìëì´ ìíì ìì ë ìëì ê°ì ê·ì¹ì´ ìë¤. ï¬ ìëì ìíì ì¸ê¸°ë를 ê³ ë ¤í´ì ì´ë ìíì ììì§ ì ííë¤. ï¬ ìíì ì´ë¤ ììì´ ì¬ë ¤ì§ì§ë ìíì 첫 ìëì´ ìì ë 모ë¶í¬ ð»ìì ìì íë를 ë½ìì¼ë¡ì ê²°ì íë¤. ï¬ ìíì ì¸ê¸°ëë ìì ìë ì¬ëì ìì ë¹ë¡íê³ , ìëì ë¹ì´ìë ìíì ê³ ë¥¼ ì ìë¤. ë¹ ìíì ì¸ê¸°ëë ì§ ì¤ íë¼ë¯¸í° ð¼ì ë¹ë¡íë¤. 첫ë²ì§¸ ìëì ë¹ì´ìë ìíì ìì ê²ì´ë¤. ëë²ì§¸ ìëì 첫ë²ì§¸ ìíì ìê±°ë, ë¹ì´ìë ìë¡ì´ ìíì ìëë¤. ë§ì½ ð¼ê° í¬ë¤ë©´ ë¹ì´ìë ìíì ê³ ë¥¼ íë¥ ì´ ëìì§ë¤. (ëë ìíì ì¸ê¸°ê° ë®ìë) ì´ë ê² ìëì´ ë¬´íí ê³ì ë¤ì´ì¤ë¤ë³´ë©´ ìíì ê°ìê° ì í´ì§ê³ (countably infinite), ìíì ì¸ê¸°ë ë¹ì¨ë ì¼ì ê°ì ìë ´íê² ëë¤. ì´ë ê² ì»ì ì¸ê¸°ëì ë¹ë 모ë¶í¬ê° ð», ì§ì¤ íë¼ë¯¸í°ê° ð¼ì¸ ë리í´ë íë¡ì¸ì¤ ìì ë½ì ìíì´ ëë¤.
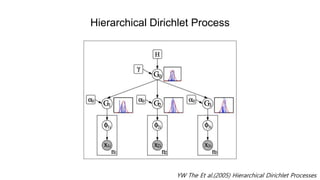
- 52. Hierarchical Dirichlet Process DPì ì ë¡ì¬í : ë§ì½ ì¤êµì§ì´ í ê³³ì´ ìëê³ ì¬ë¬ê³³ì´ë¼ê³ ìê°íì. ì´ë¤ ììì´ ì¬ë ¤ì§ ìíì ì°¾ìì ê°ê°ì ì¤êµì§ìì ê·¸ ììì´ ì¼ë§ë ì¸ê¸° ìëì§ íì¸íê³ ì¶ë¤ê³ íì. 문ì ë ì¬ê¸°ì ë°ìíë¤. ê° ì¤êµ ì§ì ìíì´ ëª ê° ìëì§ ëª¨ë¥´ê³ , ê° ìíì ì´ë¤ ììì´ ìëì§ ëª¨ë¥¸ë¤. ì´ë¤ ììì´ ìë¡ ë¤ë¥¸ ìë¹ìì ê°ì´ ë±ì¥íë¤ë ë³´ì¥ë ìë¤. ìë¹ ê° ìì ë¹êµê° ë¶ê°ë¥íë¤. ê·¸ëì íìë¤ì Hierarchical Dirichlet Process를 ì ìíë¤. ðº0~ð·ð ð¾, ð» ðºð~ð·ð(ð¼, ðº0) 모ë¶í¬ë¥¼ ë°ë¥´ë ìì ë리í´ë íë¡ì¸ì¤ë¥¼ ìì±íê³ , ì´ ë리í´ë íë¡ì¸ì¤ë¥¼ 모ë¶í¬ë¡ íë íì ëë¦¬í´ ë íë¡ì¸ì¤ë¥¼ ì¬ë¬ ê° ìì±íë¤. ì´ë°ìì¼ë¡ íì ë리í´ë íë¡ì¸ì¤ë¥¼ ìë¡ ì°ê²° ìì¼ì¤ë¤.
- 53. Hierarchical Dirichlet Process YW The Et al.(2005) Hierarchical Dirichlet Processes
- 54. CRP using HDP ì¤êµì§ ì²´ì¸ì ì´ ìë¤. ì²´ì¸ì ìë 무ìí ë§ì ìíì´ ìê³ , ê·¸ ìíìë 무ìí ë§ì ìë¦¬ê° ìë¤. ê° ì²´ì¸ ì ë§ë¤ ìëì´ íëª ì© ê¾¸ì¤í ë¤ì´ìì ìíì ê³¨ë¼ ìëë¤. ê°ê°ì ì²´ì¸ì ì ììì ë°°ë¶í´ì£¼ë ì¤êµì§ 본 ì¬ê° ìë¤. ê° ì²´ì¸ì ì ìëì´ ë¹ ìíì ìê² ëë©´, ì§ìì´ ë³¸ì¬ë¡ ê°ì ìíì ì¬ë¦´ ììì 골ë¼ì¨ë¤. 본 ì¬ìë ììì´ ë´ê²¨ìë ì주 í° ì ìê° ë¬´íí ìê³ , ê° ì ìë 충ë¶í 커ì 무íí ììì í ì ìë¤.
- 55. CRP using HDP [ðº0~ð·ð ð¾, ð» ] ï¬ ì§ìì ì ìì ì¸ê¸°ë를 ê³ ë ¤í´ì ì´ë ì ììì ììì íì§ ê²°ì ï¬ ì ìì ì´ë¤ ììì´ ì¬ë ¤ì§ì§ë ì ììì 첫 ì§ìì´ ììì í ë, 모ë¶í¬ ð»ìì ììì íë ë½ìì¼ë¡ ê²°ì ï¬ ì ìì ì¸ê¸°ëë ììì í¸ë ì§ìì ìì ë¹ë¡íê³ , ì§ìì´ ë¹ì´ìë ì ì를 ê³ ë¥¼ ìë ìë¤. ì ìì ì¸ê¸°ëë ì§ì¤ íë¼ë¯¸í° ð¾ì ìê´ìë¤. [ðºð~ð·ð(ð¼, ðº0)] ï¬ ìëì ìíì ì¸ê¸°ë를 ê³ ë ¤í´ì ì´ë ìíì ììì§ë¥¼ ê³ ë¥¸ë¤. ï¬ ìíì ì´ë¤ ììì´ ì¬ë ¤ì§ì§ë ìíì 첫 ìëì´ ìì¼ë©´ ì§ìì 본ì¬ë¡ ë³´ë´ì ê²°ì íê³ , ê·¸ ììì ë¶í¬ ìì ì§ìë¤ì´ ì ììì ììì í¸ë ë¶í¬ ðº0를 ë°ë¥¸ë¤. (ìíìë 1ê°ì ììë§ ì¬ë¼ê°ë¤) ï¬ ìíì ì¸ê¸°ëë ìì ìë ì¬ëì ìì ë¹ë¡íê³ , ì§ì¤ íë¼ë¯¸í° ð¼ì ë°ë¼ì ë¹ì´ìë ìíì ê³ ë¥¼ìë ìë¤.
- 56. CRP using HDP YW The Et al.(2005) Hierarchical Dirichlet Processes
- 57. HDP for infinite topic models ï¬ ì¤êµì§ ì²´ì¸ì â Documents ï¬ ë³¸ì¬ìì ê²°ì í´ì£¼ë ìì â Topic ï¬ ê°ê°ì ìëë¤ â Words in a document https://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture20.pdf








































![CRP using HDP
[ðº0~ð·ð ð¾, ð» ]
ï¬ ì§ìì ì ìì ì¸ê¸°ë를 ê³ ë ¤í´ì ì´ë ì ììì ììì íì§ ê²°ì
ï¬ ì ìì ì´ë¤ ììì´ ì¬ë ¤ì§ì§ë ì ììì 첫 ì§ìì´ ììì í ë, 모ë¶í¬ ð»ìì ììì íë ë½ìì¼ë¡ ê²°ì
ï¬ ì ìì ì¸ê¸°ëë ììì í¸ë ì§ìì ìì ë¹ë¡íê³ , ì§ìì´ ë¹ì´ìë ì ì를 ê³ ë¥¼ ìë ìë¤. ì ìì ì¸ê¸°ëë
ì§ì¤ íë¼ë¯¸í° ð¾ì ìê´ìë¤.
[ðºð~ð·ð(ð¼, ðº0)]
ï¬ ìëì ìíì ì¸ê¸°ë를 ê³ ë ¤í´ì ì´ë ìíì ììì§ë¥¼ ê³ ë¥¸ë¤.
ï¬ ìíì ì´ë¤ ììì´ ì¬ë ¤ì§ì§ë ìíì 첫 ìëì´ ìì¼ë©´ ì§ìì 본ì¬ë¡ ë³´ë´ì ê²°ì íê³ , ê·¸ ììì ë¶í¬ ìì
ì§ìë¤ì´ ì ììì ììì í¸ë ë¶í¬ ðº0를 ë°ë¥¸ë¤. (ìíìë 1ê°ì ììë§ ì¬ë¼ê°ë¤)
ï¬ ìíì ì¸ê¸°ëë ìì ìë ì¬ëì ìì ë¹ë¡íê³ , ì§ì¤ íë¼ë¯¸í° ð¼ì ë°ë¼ì ë¹ì´ìë ìíì ê³ ë¥¼ìë ìë¤.](https://image.slidesharecdn.com/topicmodels-190812083121/85/Topic-models-55-320.jpg)

