topology of surface
•
2 likes•578 views
This document outlines the course objectives for an introduction to 3D modeling and visualization class. The course will be taught on Tuesdays from 6-9pm for 3 credits. Topics that will be covered include NURBS surfaces, topology, Riemannian manifolds, the Moebius strip, Klein bottle, thickening surfaces, the human ear, dissection, and the work of Andreas Vesalius. The goal is to move from basic surface modeling to modeling anatomical structures.
topology of surface
- 1. Pratt Institute _School of Architecture _Sensation Tectonics Arch 522C.09/.10: _Introduction to 3D Modeling and Visualization _Instructor: _Robert Brackett _Robert.Brackett3@gmail.com _Instruction: _Tuesdays , 6:00 – 9:00 _Credits: _03 _Classification: _Elective
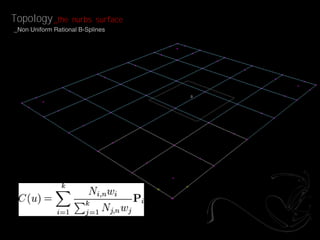
- 2. Topology _the nurbs surface _Non Uniform Rational B-Splines
- 3. Topology _the nurbs surface
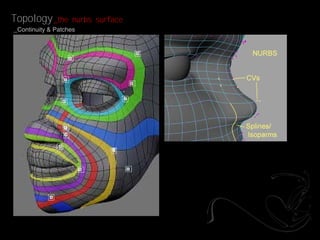
- 5. Topology _the nurbs surface _Continuity & Patches
- 6. Topology _the nurbs surface _Manifolds _Riemannian Manifolds To measure distances and angles on manifolds, the manifold must be Riemannian. A Riemannian manifold is a differentiable manifold in which each tangent space is equipped with an inner product 〈⋅,⋅〉 in a manner which varies smoothly from point to point. Given two tangent vectors u and v, the inner product 〈u,v〉 gives a real number. The dot (or scalar) product is a typical example of an inner product. This allows one to define various notions such as length, angles, areas (or volumes), curvature, gradients of functions and divergence of vector fields.
- 7. Topology _the nurbs surface
- 8. Topology _the nurbs surface
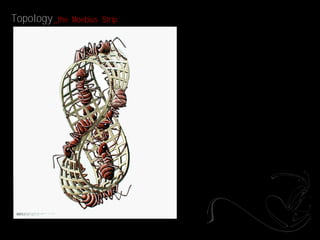
- 9. Topology _the Moebius Strip
- 10. Topology _the Moebius Strip
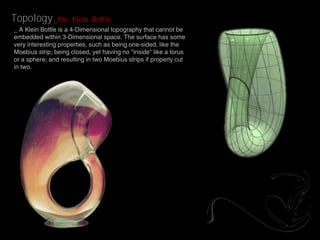
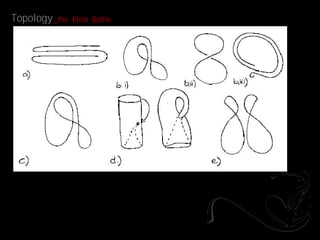
- 11. Topology _the Klein Bottle _ A Klein Bottle is a 4-Dimensional topography that cannot be embedded within 3-Dimensional space. The surface has some very interesting properties, such as being one-sided, like the Moebius strip; being closed, yet having no "inside" like a torus or a sphere; and resulting in two Moebius strips if properly cut in two.
- 12. Topology _the Klein Bottle
- 13. Topology
- 14. Topology _Thickening the Surface
- 15. Topology _Thickening the Surface
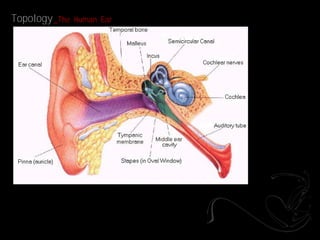
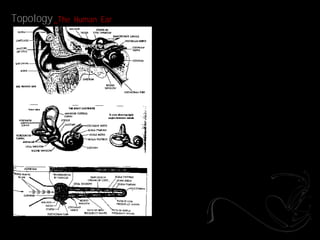
- 16. Topology _The Human Ear
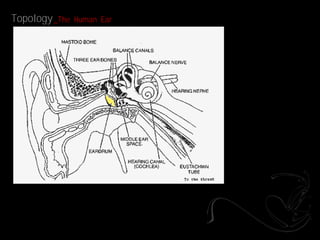
- 17. Topology _The Human Ear
- 18. Topology _The Human Ear
- 20. Topology _from Surface to Flesh
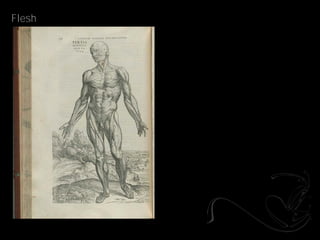
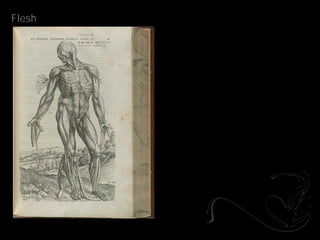
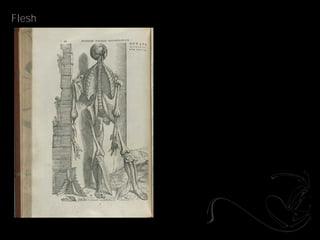
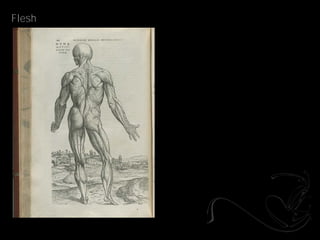
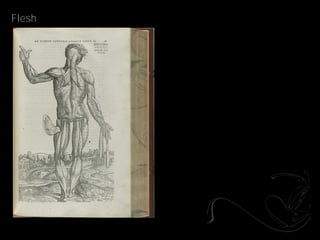
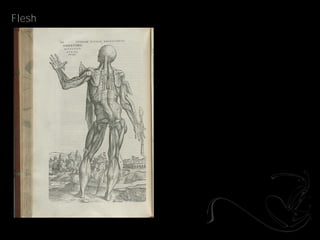
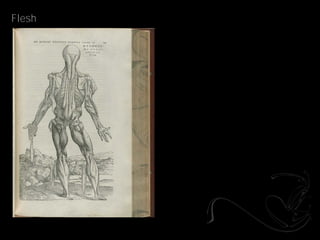
- 21. Topology _Andreas Vesalius
- 22. Flesh
- 23. Flesh
- 24. Flesh
- 25. Flesh
- 26. Flesh
- 27. Flesh
- 28. Flesh
- 29. Flesh
- 30. Flesh
- 31. Flesh
- 32. Flesh
- 33. Flesh
- 34. Flesh