![GeoGebra-bildet
3 1 6 4 75 2
1 Verktøylinja. Hvert ikon har en trekant i nederste høyre hjørne. Ved å klikke på denne
trekanten får du fram flere verktøyer. Vi skal se på disse etter hvert.
2 Angreknapp. Ved å klikke på disse pilene, kan du gå ett skritt fram eller ett tilbake for
hvert klikk.
3 Algebrafeltet. Her kommer likningene eller funksjonsuttrykkene som du har skrevet
inn i inntastingsfeltet (6). Her ser vi også lengder på linjestykker, areal av mangekanter
og alle målinger eller utregninger som du ber programmet om å utføre.
4 Grafikkfeltet. Her får du tegnet geometriske figurer eller grafer. Du kan vise eller skjule
aksene og rutenett ved å klikke på Vis og fjerne eller vise haker framfor disse ordene i
menyen. Ved å høyreklikke på grafikkfeltet kan du forandre på verdiene langs aksene og
justere mange andre egenskaper.
5 Regnearket. Dette fungerer mye på samme måten som et vanlig regneark, men har
færre muligheter enn for eksempel Excel og Calc. Fordelen med dette regnearket er at
de fungerer dynamisk sammen med verdier i Algebrafeltet og i Grafikkfeltet.
6 Inntastingsfeltet («skriv inn»). I dette feltet skriver du inn kommandoer for å få fram
det du ønsker på grafikkfeltet og i algebrafeltet. Du kan for eksempel skrive Avstand[A,B]
og trykke Enter. Da får du avstanden mellom de to punktene A og B som du har plassert
på grafikkfeltet på forhånd.
7 Kommandofeltet. Dersom du klikker på pila til høyre for dette feltet kommer det fram
en alfabetisk kommandomeny som du kan velge fra. Velger du for eksempel Midtpunkt,
kommer Midtpunkt[] fram i inntastingfeltet. Da trykker du Enter for å komme mellom
parentesene og skriver inn navnet på et linjestykke eller to punkter. For eksempel
Midtpunkt[a] eller Midtpunkt[A,B]. Da får du tegnet et punkt som ligger midt på
linjestykket a eller et punkt som ligger midt mellom A og B. Du får koordinatene til dette
midtpunktet i algebrafeltet.](https://image.slidesharecdn.com/torsteingarseggeogebra-120918155757-phpapp01/85/Torstein-Garseg-Geogebra-2-320.jpg)
![Lage verditabeller og tegne grafer
Vi skal lage verditabell til funksjonen f(x) = x^2-1 og tegne grafen.
1. hent regneark fra «vis»-meny helt øverst
2. Skriv inn de to første x-verdiene i tabellen. Dra og slipp for å få hele kolonnen med ønskede
x-verdier
3. skriv=(A1)^2-1i celle A2 (du har nå lagt inn en formel) og trykk enter
4. «dra og slipp» celle A2 (nedover i kollonne 2) så oppdager du at alle funksjonsverdier
automatisk blir lagt til for de ulike x- verdiene.
5. Merk begge kolonnene samtidig og høyreklikk. Velg «lag» og deretter «liste med punkter»
Punktene kommer nå til synet i bildet.
For å få frem grafen til f(x) skriver du funksjonsuttrykket inn i «skriv inn»-feltet og trykker
enter (eller: regpoly[Liste1,2] , altså å utføre en polynomregresjon med grad 2)
Oppgave:
Lag verditabell for funksjonen f(x)= - x^2+2 (velg x-verdier mellom -3 og
3) og tegn inn punktene i grafikkfeltet. Tegn til slutt grafen til f(x)](https://image.slidesharecdn.com/torsteingarseggeogebra-120918155757-phpapp01/85/Torstein-Garseg-Geogebra-11-320.jpg)
Torstein Garseg Geogebra
- 1. GeoGebra(digitalt verktøy i matematikk) Et nyttig verktøy for alle matematikklærere for å konkretisere og visualisere matematikk.Er også et CAS-verktøy. Helt gratis å laste ned fra www.geogebra.org GeoGebra har utkommet i flere utgaver og jeg bruker utgaven som heter: GeoGebra 4.0.0.0 Nyttige bøker: «GeoGebra for lærere», Henning Bueie,universitetsforlaget 2011 Nyttige nettsteder: www.sinus.cappelen.no (her finner du en god veiledning i bruk av geogebra) www.geogebra.no (god veiledning i bruk, og da også rettet mot ungdomsskolen, har også gode manualer) Av veldig mange muligheter som ligger i GeoGebra så har jeg valgt ut noen få aktuelle konkretiseringer med utgangspunkt i læreplanmål for grunnskolen. På kurset så rekker vi nok ikke å ta for oss alle eksemplene men de fleste.I slutten av de fleste eksempler har jeg laget en oppgave som dere selv kan prøve på. Jeg mener at GeoGebra er et fantastisk pedagogisk verktøy for oss lærere til å få konkretisert emnene geometri, funksjonslære, algebra og tallregning på en slik måte at det skaper økt motivasjon. I NYGIV-ånd så er det motivasjonsstimulerende og læringsfremmende metoder vi skal arbeide med i matematikktimene. Jeg skal prøve å gi dere et første innblikk i hvilke muligheter som ligger her med tanke på å øke motivasjon blant elever for faget i ungdomsskolen gjennom å vise noen eksempler innenfor geometri og funksjonslære. Bruk eksemplene mineog dine egne lagde eksempler i undervisningen! Torstein Garseg 14/9-12
- 2. GeoGebra-bildet 3 1 6 4 75 2 1 Verktøylinja. Hvert ikon har en trekant i nederste høyre hjørne. Ved å klikke på denne trekanten får du fram flere verktøyer. Vi skal se på disse etter hvert. 2 Angreknapp. Ved å klikke på disse pilene, kan du gå ett skritt fram eller ett tilbake for hvert klikk. 3 Algebrafeltet. Her kommer likningene eller funksjonsuttrykkene som du har skrevet inn i inntastingsfeltet (6). Her ser vi også lengder på linjestykker, areal av mangekanter og alle målinger eller utregninger som du ber programmet om å utføre. 4 Grafikkfeltet. Her får du tegnet geometriske figurer eller grafer. Du kan vise eller skjule aksene og rutenett ved å klikke på Vis og fjerne eller vise haker framfor disse ordene i menyen. Ved å høyreklikke på grafikkfeltet kan du forandre på verdiene langs aksene og justere mange andre egenskaper. 5 Regnearket. Dette fungerer mye på samme måten som et vanlig regneark, men har færre muligheter enn for eksempel Excel og Calc. Fordelen med dette regnearket er at de fungerer dynamisk sammen med verdier i Algebrafeltet og i Grafikkfeltet. 6 Inntastingsfeltet («skriv inn»). I dette feltet skriver du inn kommandoer for å få fram det du ønsker på grafikkfeltet og i algebrafeltet. Du kan for eksempel skrive Avstand[A,B] og trykke Enter. Da får du avstanden mellom de to punktene A og B som du har plassert på grafikkfeltet på forhånd. 7 Kommandofeltet. Dersom du klikker på pila til høyre for dette feltet kommer det fram en alfabetisk kommandomeny som du kan velge fra. Velger du for eksempel Midtpunkt, kommer Midtpunkt[] fram i inntastingfeltet. Da trykker du Enter for å komme mellom parentesene og skriver inn navnet på et linjestykke eller to punkter. For eksempel Midtpunkt[a] eller Midtpunkt[A,B]. Da får du tegnet et punkt som ligger midt på linjestykket a eller et punkt som ligger midt mellom A og B. Du får koordinatene til dette midtpunktet i algebrafeltet.
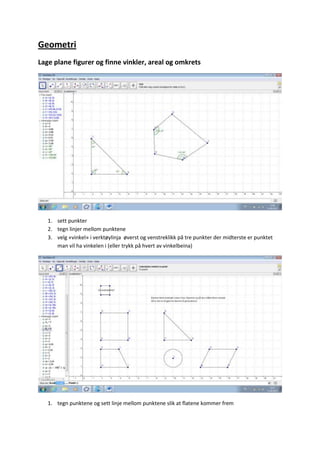
- 3. Geometri Lage plane figurer og finne vinkler, areal og omkrets 1. sett punkter 2. tegn linjer mellom punktene 3. velg «vinkel» i verktøylinja øverst og venstreklikk på tre punkter der midterste er punktet man vil ha vinkelen i (eller trykk på hvert av vinkelbeina) 1. tegn punktene og sett linje mellom punktene slik at flatene kommer frem
- 4. 2. Arealet får vi ved å velge «Areal» i kommandolisten (eller lettere, begynn å skrive Areal i «sett inn»-feltet og du velger «punkt, punkt, …..» Elevene bør da telle kvadratenheter først (lage et første overslag) før fasiten kommer. Gå fra opptelling til generalisering Eksempel: trapesareal med bruk av «penn». Oppgave: Tegn et trapes med valgfri lengde på a, b og h. Finn areal og omkrets av trapeset. Bruk «penn» og vis fremgangsmåten for utregning av arealet direkte på geogebraarket.
- 5. Å vise vinkelsummen i en trekant 1. lag trekant ABC 2. sett vinklene 3. lag parallell linje med AC gjennom B 4. lag «stråle gjennom to punkt» fra A gjennom B 5. sett resten av vinklene i B 6. Trykk piltastboksen øverst og beveg punktet C eller A ved å trykke punktene med venstre musetast og holde.
- 6. Konstruksjon Oppgave: Konstruer en trekant ABC der vinkel BAC er 30˚, sidelengden AB har lengden 8 og sidelengden BC har lengden 5. Er trekanten entydig? (Tips: let i verktøylisten øverst etter «halveringslinje for vinkel» for å halvere 60)
- 7. Bevise pythagoraslæresetning ved summering av kvadratarealer 1. sett punkt A på x-aksen 2. lag normal til x-aksen gjennom A. 3. sett punkt B på x-aksen 4. sett punkt C på normalen 5. sett linje mellom punktene A, B og C 6. lag regulær mangekant (4 sidig) på hver av trekantens sidelengder. Arealet til hvert kvadrat kommer til syne i algebravinduet 7. velg «pilmarkøren» og beveg punkt A og C Konklusjon: Summen av kvadratene på katetene er det samme som arealet til kvadatet på hypotenusen. (AB)^2 + (AC)^2 = (BC)^2
- 8. Hva er «pi»? Oppgave: Tegn en sirkel med radius 4 og finn forholdet mellom omkretsen og diameter
- 9. Lineære funksjoner og andregradsfunksjoner (grafer) Rette linjer (m/glidere) 1. velg «glider» (let i boksene øverst) 2. skriv a=0 i «skriv inn» feltet og trykk enter 3. skriv b=0 i «skriv inn» feltet og trykk enter 4. skriv y=a*x+b i «skriv inn» feltet og trykk enter 5. klikk på sirklene ved siden av a og b i algebravinduet (til venstre) og gliderne kommer til syne i grafikkfeltet. 6. Få frem navnene a og b på gliderne ved å høyreklikke på glidere og velge «vis navn» 7. skyv først i punktet på glideren til a og deretter b 8. Sett på «stigningstrekant» (let i verktøylisten øverst) 9. Du har nå et fint konkretiseringsverktøy til å vise betydningen av a og b i y=ax+b Oppgave: Lag en illustrasjon som får frem betydningen av a, b og c for grafens utsende til andregradsfunksjoner ved å bruke glidere. Generelt for andregradsfunksjoner f(x)=ax^2+bx+c
- 10. Løse likninger grafisk 1. skriv inn venstre side av likningen i «skriv inn»-feltet og trykk enter 2. skriv inn høyre side av likningen i «skriv inn»-feltet og trykk enter 3. Skriv «skjæring» i skriv inn feltet og (f,g) i parantesen (hvis f og g er navnet på linjene som er tegnet). Trykk enter og løsningen synes i grafikkfeltet og i algebrafeltet. Oppgave: Løs likningen grafisk X^2-2x-1=x-1
- 11. Lage verditabeller og tegne grafer Vi skal lage verditabell til funksjonen f(x) = x^2-1 og tegne grafen. 1. hent regneark fra «vis»-meny helt øverst 2. Skriv inn de to første x-verdiene i tabellen. Dra og slipp for å få hele kolonnen med ønskede x-verdier 3. skriv=(A1)^2-1i celle A2 (du har nå lagt inn en formel) og trykk enter 4. «dra og slipp» celle A2 (nedover i kollonne 2) så oppdager du at alle funksjonsverdier automatisk blir lagt til for de ulike x- verdiene. 5. Merk begge kolonnene samtidig og høyreklikk. Velg «lag» og deretter «liste med punkter» Punktene kommer nå til synet i bildet. For å få frem grafen til f(x) skriver du funksjonsuttrykket inn i «skriv inn»-feltet og trykker enter (eller: regpoly[Liste1,2] , altså å utføre en polynomregresjon med grad 2) Oppgave: Lag verditabell for funksjonen f(x)= - x^2+2 (velg x-verdier mellom -3 og 3) og tegn inn punktene i grafikkfeltet. Tegn til slutt grafen til f(x)
- 12. Nullpunkter, toppunkter, bunnpunkter, tangentlinjer 1. Topp/bunnpunkt: Skriv «ekstremalpunkt» i skriv inn-feltet og f i parantesen som dukker opp. Trykk enter (hva ser du i bildet og i algebrafeltet?). 2. Nullpunkt: Skriv «nullpunkt» i skriv inn- feltet og trykk enter. 3. Tangentlinje: Sett et vilkårlig punkt på grafen. Velg deretter «tangentlinje» i en av verktøyboksene øverst. Trykk så på punktet du satte og deretter valgfritt sted på grafen og tangentlinjen dukker opp Dra i det satte punktet. Hva ser du? Oppgave Tegn grafen til funksjonen f(x)= - x^2-x+2 Finn toppunkt og nullpunkter Tegn en tangentlinje på grafen i punktet (1, f(1)) med stigningstrekant og undersøk med den vekstfarten i toppunktet til grafen