Towards Semantometrics: A New Semantic Similarity Based Measure for Assessing a Research Publication's Contribution
•
2 likes•569 views
ºÝºÝߣs for a presentation at the Third International Workshop on Mining Scientific Publications @ JCDL 2014 Paper: http://www.dlib.org/dlib/november14/knoth/11knoth.html Paper abstract: We propose Semantometrics, a new class of metrics for evaluating research. As opposed to existing Bibliometrics,Webometrics, Altmetrics, etc., Semantometrics are not based on measuring the number of interactions in the scholarly communication network, but build on the premise that full-text is needed to assess the value of a publication. This paper presents the first Semantometric measure, which estimates the research contribution. We measure semantic similarity of publications connected in a citation network and use a simple formula to assess their contribution. We carry out a pilot study in which we test our approach on a small dataset and discuss the challenges in carrying out the analysis on existing citation datasets. The results suggest that semantic similarity measures can be utilised to provide meaningful information about the contribution of research papers that is not captured by traditional impact measures based purely on citations.
![/15
Problems of current impact metrics
•  Sen-ment, seman-cs, context and mo-ves [Nicolaisen, 2007]
•  Popularity and size of research communi-es [Brumback,
2009; Seglen, 1997]
•  Time delay [Priem and Hemminger, 2010]
•  Skewness of the distribu-on [Seglen, 1992]
•  Differences between types of research papers [Seglen, 1997]
•  Ability to game/manipulate cita-ons [Arnold and Fowler,
2010; Editors, 2006]
3](https://image.slidesharecdn.com/wosp2014presentation-151223101149/85/Towards-Semantometrics-A-New-Semantic-Similarity-Based-Measure-for-Assessing-a-Research-Publication-s-Contribution-3-320.jpg)
Towards Semantometrics: A New Semantic Similarity Based Measure for Assessing a Research Publication's Contribution
- 3. /15 Problems of current impact metrics •  Sen-ment, seman-cs, context and mo-ves [Nicolaisen, 2007] •  Popularity and size of research communi-es [Brumback, 2009; Seglen, 1997] •  Time delay [Priem and Hemminger, 2010] •  Skewness of the distribu-on [Seglen, 1992] •  Differences between types of research papers [Seglen, 1997] •  Ability to game/manipulate cita-ons [Arnold and Fowler, 2010; Editors, 2006] 3
- 4. /15 Alterna-ve metrics •  Alt-/Webo-metrics etc. –  Impact s-ll dependent on the number of interac-ons in a scholarly communica-on network •  Full-text (Semantometrics) –  Contribu-on to the discipline dependent on the content of the manuscript. 4
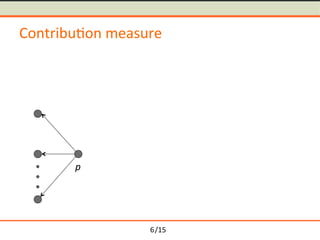
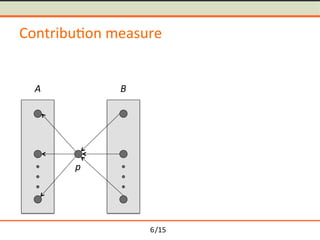
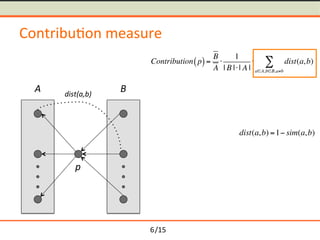
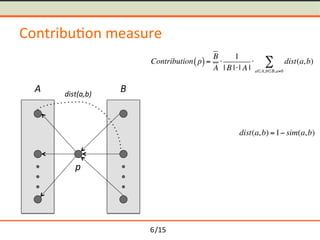
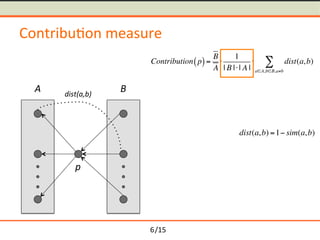
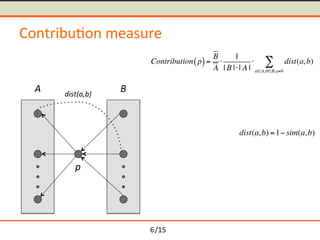
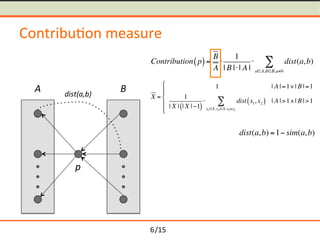
- 14. /15 Contribu-on measure p A B Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ 6
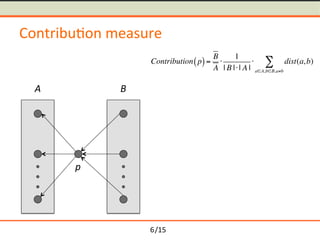
- 15. /15 Contribu-on measure p A B Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ 6
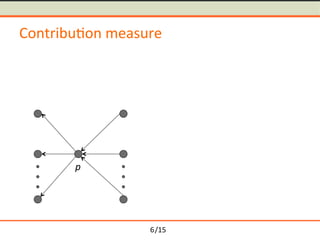
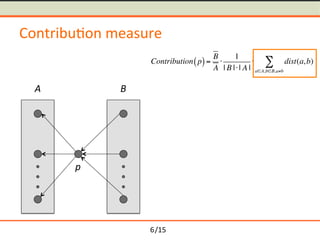
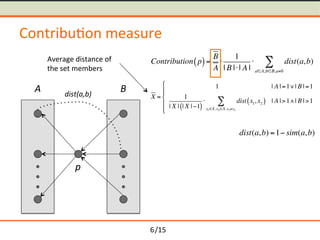
- 16. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ 6
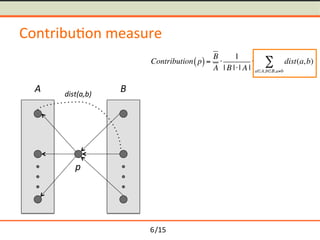
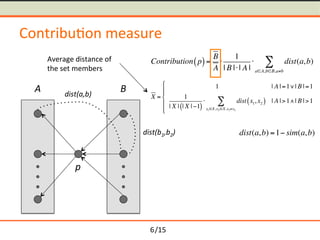
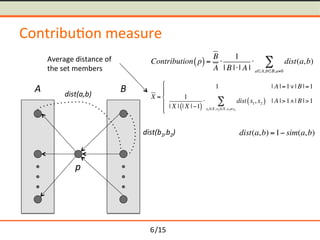
- 17. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ dist(a,b) =1− sim(a,b) 6
- 18. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ dist(a,b) =1− sim(a,b) 6
- 19. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ dist(a,b) =1− sim(a,b) 6
- 20. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ dist(a,b) =1− sim(a,b) 6
- 21. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ dist(a,b) =1− sim(a,b) 6
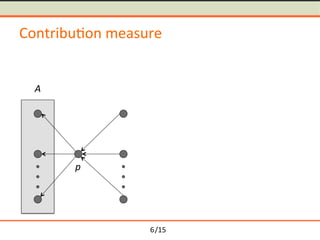
- 22. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ⎧ ⎨ ⎪ ⎩ ⎪ dist(a,b) =1− sim(a,b) 6
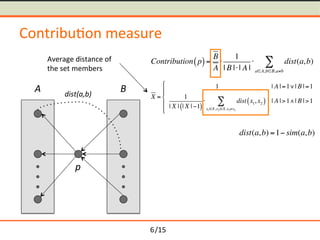
- 23. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ⎧ ⎨ ⎪ ⎩ ⎪ dist(a,b) =1− sim(a,b) Average distance of the set members 6
- 24. /15 Contribu-on measure p A B dist(a,b) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ( ) * + * dist(a,b) =1− sim(a,b) Average distance of the set members 6
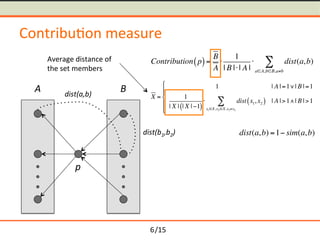
- 25. /15 Contribu-on measure p A B dist(a,b) dist(b1,b2) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ( ) * + * dist(a,b) =1− sim(a,b) Average distance of the set members 6
- 26. /15 Contribu-on measure p A B dist(a,b) dist(b1,b2) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ( ) * + * dist(a,b) =1− sim(a,b) Average distance of the set members 6
- 27. /15 Contribu-on measure p A B dist(a,b) dist(b1,b2) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ( ) * + * dist(a,b) =1− sim(a,b) Average distance of the set members 6
- 28. /15 Contribu-on measure p A B dist(a,b) dist(b1,b2) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ( ) * + * dist(a,b) =1− sim(a,b) Average distance of the set members 6
- 29. /15 Contribu-on measure p A B dist(a,b) dist(b1,b2) Contribution p( )= B A ⋅ 1 | B |⋅| A | ⋅ dist(a,b) a∈A,b∈B,a≠b ∑ X = 1 | A |=1∨| B |=1 1 | X | | X |−1( ) ⋅ dist x1, x2( ) x1∈X,x2 ∈X,x1≠x2 ∑ | A |>1∧| B |>1 ( ) * + * dist(a,b) =1− sim(a,b) Average distance of the set members 6
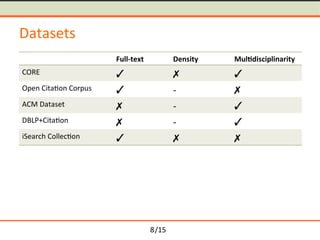
- 31. /15 Datasets Full-text Density Mul5disciplinarity CORE ✓ ✗ ✓ Open Cita-on Corpus ✓ - ✗ ACM Dataset ✗ - ✓ DBLP+Cita-on ✗ - ✓ iSearch Collec-on ✓ ✗ ✗ 8
- 32. /15 Our dataset •  10 seed publica-ons from CORE with varying level of cita-ons •  missing ci-ng and cited publica-ons downloaded manually •  only freely accessible English documents were downloaded •  in total 716 documents (~50% of the complete network) •  2 days to gather the data 9
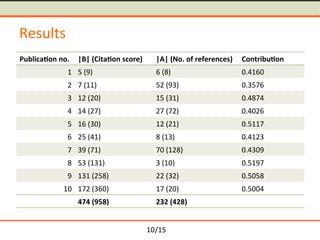
- 33. /15 Results Publica5on no. |B| (Cita5on score) |A| (No. of references) Contribu5on 1 5 (9) 6 (8) 0.4160 2 7 (11) 52 (93) 0.3576 3 12 (20) 15 (31) 0.4874 4 14 (27) 27 (72) 0.4026 5 16 (30) 12 (21) 0.5117 6 25 (41) 8 (13) 0.4123 7 39 (71) 70 (128) 0.4309 8 53 (131) 3 (10) 0.5197 9 131 (258) 22 (32) 0.5058 10 172 (360) 17 (20) 0.5004 474 (958) 232 (428) 10
- 34. /15 Results 11
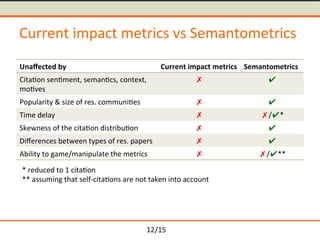
- 35. /15 Current impact metrics vs Semantometrics Unaffected by Current impact metrics Semantometrics Cita-on sen-ment, seman-cs, context, mo-ves ✗ ✔ Popularity & size of res. communi-es ✗ ✔ Time delay ✗ ✗/✔* Skewness of the cita-on distribu-on ✗ ✔ Differences between types of res. papers ✗ ✔ Ability to game/manipulate the metrics ✗ ✗/✔** * reduced to 1 cita-on ** assuming that self-cita-ons are not taken into account 12
- 36. /15 Conclusions •  Full-text necessary •  Semantometrics are a new class of methods •  We showed one method to assess the research contribu-on 13
- 37. /15 References •  Jeppe Nicolaisen. 2007. Cita-on Analysis. Annual Review of Informa-on Science and Technology, 41(1):609-641. •  Douglas N Arnold and Kris-ne K Fowler. 2010. Nefarious numbers. No-ces of the American Mathema-cal Society, 58(3):434-437. •  Roger A Brumback. 2009. Impact factor wars: Episode V -- The Empire Strikes Back. Journal of child neurology, 24(3):260-2, March. •  The PLoS Medicine Editors. 2006. The impact factor game. PLoS medicine, 3(6), June. 14
- 38. /15 References •  Jason Priem and Bradely M. Hemminger. 2010. Scientometrics 2.0: Toward new metrics of scholarly impact on the social Web. First Monday, 15(7), July. •  Per Omar Seglen. 1992. The Skewness of Science. Journal of the American Society for Informa-on Science, 43(9):628-638, October. •  Per Omar Seglen. 1997. Why the impact factor of journals should not be used for evalua-ng research. BMJ: Bri-sh Medical Journal, 314(February):498-502. 15