Tps04
Download as PPTX, PDF
0 likes953 views
Queuing theory is used to determine optimal service levels by using mathematical formulas and simulations to calculate variables like wait times and average service times based on arrival rates and facility capacities. It was originally developed for telephone systems but is now used in various contexts like manufacturing, transportation, and more. Key aspects of queuing systems include arrival patterns, service disciplines, number of service channels, service times, system capacities, and customer abandonment behavior. Common queuing models include the single-channel M/M/1 model and multiple-channel M/M/s models.
Tps04
- 2. Queuing is techniques developed by the study of people standing in line to determine the optimum level of service provision. In queuing theory, mathematical formulae, or simulations, are used to calculate variables such as length of time spent standing in line and average service time, which depend on the frequency and number of arrivals and the facilities available. The results enable decisions to be made on the most cost-effective level of facilities and the most efficient organization of the process. Early developments in queuing theory were applied to the provision of telephone switching equipment but the techniques are now used in a wide variety of contexts, including machine maintenance, production lines, and air transportation.M. Sitepu2Antrian
- 3. Queuing theory deals with problems that involve queuing (or waiting). Some examples of queuing include:Banks or supermarketscustomers waiting for service
- 4. Computersusers waiting for a response
- 5. Public transportationriders waiting for a bus/train
- 6. Failure situationsmachinery owners waiting for a failure to occurQueues form because resources are limited. In fact, it makes economic sense to have queues.In designing queuing systems, a balance is needed between service to customers (which means short queues and implies many servers) and cost (too many servers waste funds).Most queuing systems can be divided into individual sub-systems, consisting of entities queuing for some activity.M. Sitepu3Antrian
- 7. Queuing theory applies to any system in equilibrium, as long as nothing in the black box is creating or destroying tasks (arrivals=departures).M. Sitepu4Antrian
- 8. Queuing theory mathematics gets very complicated because it applies probability and statistics to queuing systems.What is the probability that the arriving task will find a device busy?On average, how many tasks are ahead of the task that just entered the system?The Early DerivationsA single server queue is a combination of a servicing facility that accommodates one customer at a time (server) + a waiting area (queue).These components together are called a system.M. Sitepu5Antrian
- 9. The early queuing work treated the system as a single homogeneous server, without regard to discrete components or types of workloads. These systems were called M/M/1 queues.Later, this work was expanded to include multiple homogeneous servers inside the black box.Queuing MethodsFour types of queuing techniques commonly implementedFirst in First Out (FIFO).Weighted Fair QueuingCustom QueuingPriority QueuingM. Sitepu6Antrian
- 10. First In First Out (FIFO)Packets are transmitted in the order in which they arrive.Single Queue, Packet droppingWeighted Fair Queuing (WFQ)Packets are classified into different "conversation messages
- 11. Each queue has some priority value or weight assigned to it.
- 12. Low volume traffic is given higher priority over high volume traffic
- 13. After accounting for high priority traffic the remaining bandwidth is divided fairly among multiple queues (if any) of low priority traffic.M. Sitepu7Antrian
- 14. Custom QueuingSeparate queues maintained for separate classes of traffic.
- 15. The algorithm requires a byte count to be set per queue.
- 16. That many bytes rounded of to the nearest packet is scheduled for delivery.
- 17. This ensures that the minimum bandwidth requirement by the various classes of traffic is met.
- 18. CQ round robins through the queues, picking the required number of packets from each.
- 19. If a queue is of length 0 then the next queue is serviced.M. Sitepu8Antrian
- 20. Priority Queuing4 traffic priorities Defined.- high, medium, normal and low.
- 21. Incoming traffic is classified and enqueued in either of the 4 queues.
- 23. Unclassified packets are put in the normal queue.
- 24. The queues are emptied in the order of - high, medium, normal and low. In each queue, packets are in the FIFO orderM. Sitepu9Antrian
- 25. Queuing Networks After much more work in the queuing theory field (approximately 20 years), a new technique was developed that divided computer system into networks of queues.MVAThis new technique is called Mean Value Analysis. It allowed a computer system to be segregated by workload classes(transactions, arrival rates, numbers of clients) as well as components (CPU, disk, etc.)Systems were also delineated as being open or closed.M. Sitepu10Antrian
- 26. Mean value analysis is an iterative approach of solving three primary equations for class r workload at queue i.The three equations provide solutions for the residence time (response time, per class, per queue), the throughput, and the queue length (number of class r tasks at queue i).Software and hardware contention can be modeled using these techniques.M. Sitepu11Antrian
- 27. Model AntrianSederhana1.Pendahuluan2.Struktur Model Antrian (The Structure of Queuing Model)3. Single-Channel Model4. Multiple-Channel Model5. Model BiayaMinimum (Cost Minimization Models)6. Non-Poisson Model7. Model Self Service Facilities8. Model Network (Queuing Network)M. Sitepu12Antrian
- 28. 1. PendahuluanSistem antrian sangat diperlukan ketika para pelanggan (konsumen) menungguuntukmendapatkanjasapelayananContohpenggunaansistemantriandalammelancarkanpelayanankepadapelangganataukonsumen :Mahasiswamenungguuntukregistrasidanpembayaranuangkuliah
- 30. Para calonpenumpang KA menunggupelayanandiloketpenjualantiket
- 31. Para pengendarakendaraanmenungguuntukmendapatkanpelayananpengisianbahanbakardi SPBUTeoriantriandiciptakanoleh A.K. Erlang (ahlimatematikDenmark) padatahun 1909.M. Sitepu13Antrian
- 32. 2. Struktur Model Antrian (The Structure of Queuing Model)Gambar 1. Struktur sistem antrianM. Sitepu14Antrian
- 33. Gambar 1 menunjukkan struktur umum suatu model antrian yang memiliki 2 komponen :1) Garis tungguatauantrian (queue)2) Fasilitaspelayanan (servicefacility)Gambar 2. Pelayanan nasabah di bankM. Sitepu15Antrian
- 35. ProsedurteknikantrianLangkah 1 : Tentukansistemantrianapa yang harusdipelajari.Langkah 2 : Tentukan model antrian yang sesuaidalammenggambarkansistem.ContohdalamkasuspompabensindiSPBU,terdapattiga model yang dapat digunakan :tigapompauntuk premium dengansatugaristunggu
- 37. satupompauntuk premium, satupompauntukpertamax, satupompauntuk solar denganmasing-masingmemilikigaristunggu.Langkah3 : Gunakan formula matematikataumetodesimulasiuntukmenganalisa model antrian.M. Sitepu17Antrian
- 38. Komponen dalam Sistem Antrian (lihat gambar 1)Populasimasukan (input population) :Input populasiterbatas (finite input population)
- 39. Input populasitakterbatas (infinite input population)Distribusikedatangan,Pelanggan datang setiap 5 menit (constant arrival distribution)
- 40. Pelanggandatangsecaraacak (arrival pattern random)Disiplinpelayanan,FCFS (first come, first served) dan
- 41. LCFS (last come, first served)
- 42. Pelanggandilayani secara acak dan prioritasFasilitaspelayanan, mengelompokkanfasilitaspelayananmenurutjumlah yang tersedia,Sistemsingle-channel (gambar 3)
- 44. Distribusipelayanan, ditetapkanberdasarkansatucaradariduacaraberikut :Berapabanyakpelanggan yang dapatdilayaniper satuanwaktu
- 45. Berapalama setiappelanggandapatdilayaniKapasitassistempelayanan, samadenganmemaksimumkanjumlahpelanggan yang diperkenankanmasukdalamsistem, Kapasitas terbatas atau tak terbatas.Karakteristiksistemlainnya, pelanggantidakakanmasuksistem antrian jika pelanggan lain telah banyak menunggu ataumeninggalkanantrian.Perilakuinidikatakansebagai reneging ataupengingkaran.M. Sitepu19Antrian
- 46. Notasidalamsistemantriann = Jumlahpelanggandalamsistem了 = Jumlah rata-rata pelanggan yang datang per satuan waktu亮 = Jumlah rata-rata pelanggan yang dilayani per satuanwaktuL = Jumlah rata-rata pelanggan yang diharapkan dalam sistemLq = Jumlahpelanggan yang diharapkanmenunggudalamantrianPo = Probabilitas tidak ada pelanggan dalam sistemPn = Probabilitas kepastian n pelanggan dalam sistemP = Tingkat intensitas fasilitas pelayananW = Waktu yang diharapkan oleh pelanggan selama dalam sistemWq = Waktu yang diharapkanolehpelangganselamamenunggudalamantrian1/ 亮 = Waktu rata-rata pelayanan1/ 了 = Waktu rata-rata antarkedatanganS = JumlahfasilitaspelayananM. Sitepu20Antrian
- 47. 3. Single-channel ModelModel antrian paling sederhana adalah model saluran tunggal(single-channel model) ditulis dengan notasi sistem M/M/1 M pertama : rata-rata kedatangan (distribusiprobabilitas Poisson),M kedua : tingkatpelayananAngka 1 : jumlahfasilitaspelayanansatusaluran (one channel)Gambar 3. Sistem Single ChannelM. Sitepu21Antrian
- 48. Komponen:Populasiinput takterbatasyaitujumlahkedatanganpelangganpotensialtakterbatas.Distribusi kedatangan pelanggan potensial mengikuti distribusiPoisson.Disiplin pelayanan mengikuti pedoman FCFS.Fasilitaspelayananterdiridarisalurantunggal.Distribusi pelayanan mengikuti distribusi Poisson, asumsi(了 < 亮)KapasitassistemdiasumsikantakterbatasTidak ada penolakan maupun pengingkaranProbabilitas Poisson :M. Sitepu22Antrian
- 49. Persamaandalamsistem ( M/M/1 ) :M. Sitepu23Antrian
- 50. 4. Multiple-channel ModelDalam multiple-channel model, fasilitaspelayanan yang dimilikilebihdarisatu, ditulisdengannotasi sistem M/M/s Huruf (s) menyatakanjumlahfasilitaspelayanan.Contoh 1 :Bagianregistrasisuatuuniversitasmenggunakansistemkomputerdengan4 orang operator dansetiap operator melakukanpekerjaan yang sama. Rata-rata kedatanganmahasiswa yang mengikutidistribusikedatanganPoisson adalah 100 mahasiswa per jam. Setiapoperator dapatmemproses 40 registrasimahasiswa per jam denganwaktupelayanan per mahasiswa mengikuti distribusi eksponensial.M. Sitepu24Antrian
- 51. Berapapersentasewaktumahasiswatidakdalamregistrasi ? (Po)Berapa lama rata-rata mahasiswa menghabiskan waktunya di pusat registrasi? (W)Berapalama mahasiswamenungguuntukmendapatkanpelayananregistrasi atas dasar rata-rata tsb? (Lq)Berapalama rata-rata mahasiswamenunggudalamgarisantrian? (Wq)Jika ruang tunggu pusat registrasi mahasiswa hanya mampu untuk menampung5 mahasiswa, berapapersentasewaktusetiapmahasiswaberadadalamgarisantriandiluarruangan?Penyelesaian :Digunakansistem (M/M/4)Rata-rata kedatangan mahasiswa (了) = 100Rata-rata setiap operator dapatmelayanimahasiswa(亮)= 40M. Sitepu25Antrian
- 52. a) Menggunakanpersamaan :Probabilitasmahasiswatidakdalammendatangipusatregistrasisebesar Po = 0.0737 atau 7.37 %b) Waktu rata-rata yang dihabiskanmahasiswadipusatregistrasi (W)PertamadihitungLqdenganpersamaan :M. Sitepu26Antrian
- 53. c) Waktumenunggumahasiswauntukmendapatkanpelayananregistrasiadalah:Lq = 0.533 jam = 31.98 menitd) Waktumenunggumahasiswaselamadalamprosesantrianadalah:Wq = 0.00533 jam = 0.03 menitM. Sitepu27Antrian
- 54. e) Untukmenentukanberapa lama mahasiswaberadadiluarruangantunggudilakukandenganmenghitungPnyaitumenjumlahkan: Pn= P0+P1 + P2 + P3 + P4 + P5 = 0.0737 + 0.1842 + 0.2303 + 0.1919 + 0.1200 + 0.0750 = 0.8751samadenganproporsiwaktu yang digunakanmahasiswamenunggudidalamruanganregistrasi.Persentasewaktu yang digunakanmahasiswauntukmenunggudiluarruangan adalah 1-0.8751 = 0.1249 = 12.49 % dari waktu mahasiswa.Jika mahasiswa berada dalam sistem selama 1.8 menit, maka 87.51 % dariwaktutsbmahasiswaberadadalamruangtunggudan 12.49 % atau 0.225 menitmahasiswaberadadiluarruangtunggu.M. Sitepu28Antrian
- 55. 5. Model BiayaMinimum (Cost Minimization Models)Padabeberapaaplikasisistemantriansangatmungkinmendisainsistem yang akanmeminimumkanbiaya per satuanwaktu.Persamaan biaya total per jam : TC = SC +WCTC = Total biaya per jamSC = Biayapelayanan per jamWC = Biayamenunggu per jam per pelangganTotal biayamenunggu per jam :WC =了 (W cw) = ( 了 W) cw = L cwM. Sitepu29Antrian
- 56. Total biayamenunggu per jam :WC = 了 (W cw) = ( 了 W) cw = L cwcw = biayamenungguper jamperpelangganW = waktu yang dihabiskanpelangganW cw = rata-ratabiayamenunggu per pelanggan了 = rata-ratakedatanganpelanggan per jam denganpersamaanL = 了W (persamaan--)6. Non Poisson ModelDitulis dengan notasi sistem M/G/1 M menunjukkankedatangan PoissonG merupakan rata-rata (means) waktu pelayananAngka 1 menunjukkansistemmemilikisatu channelM. Sitepu30Antrian
- 57. Dalamsistem (M/M/1) dan (M/M/s) diasumsikanbahwatingkatPelayanan (pelayananpelanggan per satuanwaktu) memilikiprobabilitasPoisson.Samadenganasumsibahwawaktupelayananpelangganmemilikiprobabilitaseksponensial.ProbabilitasPoisson sangat ideal untuk model kedatangan random.M. Sitepu31Antrian
- 58. 7. Self Service FacilitiesBanyakperusahaan (pedagang) menyediakanfasilitaspelayanansendiri (self-service facilities) bagiparapelanggannyaseperti supermarket, restoran, Perpustakaan, pompabensin, teleponumum, tokobuku, dll.M. Sitepu32Antrian
- 59. Digunakanmodel antrian (M/M/s) apabilajumlahfasilitaspelayananterbatas (finite)Digunakan model antrian (M/M/) apabilajumlahfasilitaspelayanan tak terbatas (infinite) atau tidak perlu menungguPersamaan yang digunakandalam model antrian (M/M/ ) sbb :M. Sitepu33Antrian
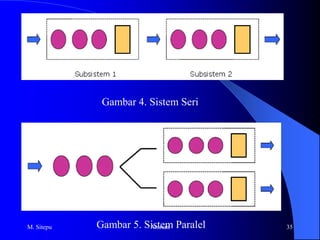
- 60. 8. Queuing NetworkModel networks dapat menggunakan sistem seri maupun sistemparalel.Sistemseriterdiridarisatusubsistemmengikutisubsistem yang lain.SetiappelangganharusmelewatisatusubsistemkemudianMelewatisubsistem yang lain sepertiregistrasimahasiswa.SistemparalelmaliputiduaataulebihsubsistemdansetiapPelanggan harus melewati satu subsistem.Sebuahsubsistemmungkinmenggunakansistemantrian (M/M/1) atausistem (M/M/s)M. Sitepu34Antrian
- 61. Gambar 4. Sistem SeriGambar 5. SistemParalelM. Sitepu35Antrian