Transportation and logistics modeling 2
Download as pptx, pdf0 likes356 views
This document discusses statistical concepts like variability, random experiments, descriptive statistics, probability distributions, and statistical data analysis. It provides examples of different probability distributions like binomial, Poisson, normal, exponential, and Weibull distributions. It also discusses the four basic steps of statistical data analysis: defining the problem, collecting the data, analyzing the data, and reporting results. Methods like hypothesis testing are discussed as part of data analysis.
Transportation and logistics modeling 2
- 1. Basics of statisticsand Data collection and analysisWeeks 2,3, and 4
- 2. Variability Statistical techniques are useful for describing and understanding variability.
- 3. Variability: Successive observations of a system or phenomenon do not produce exactly the same result.
- 4. Statistics gives us a framework for describing this variability and for learning about potential sources of variability.Nylon connector to be used in an automotive engine application.
- 5. Design specification on wall thickness at 3/32 inch
- 6. The effect of this decision on the connector pull-off force. If the pull-off force is too low, the connector may fail when it is installed in an engine.
- 7. Eight prototype units are produced and their pull-off forces measured (in pounds): 12.6, 12.9, 13.4, 12.3, 13.6, 13.5, 12.6, 13.1.Random Experiment
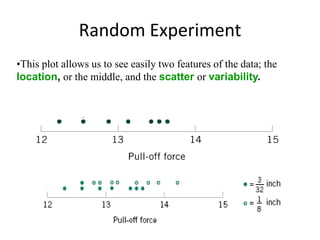
- 8. This plot allows us to see easily two features of the data; the location, or the middle, and the scatter or variability.Random Experiment
- 10. A closer examination of the system identifies deviations from the model.Random Experiment
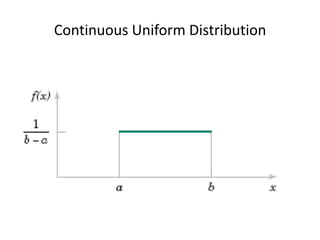
- 11. Discrete Random VariablesThey are variables which have finite (countable) range.They can not be assigned other value.Examples:Let x be your grade S={A,A-,B+,B,B-,C,D}Let y be a working day in a week S={M,T,W,R,F}Let z be your weight S={40k<z<300K} this is not discrete, it is continuous, z can be 120.63k48 digital lines are observed, x indicate how many are in use, x can be any integer from 1 to 48.Note x can not be 1.5
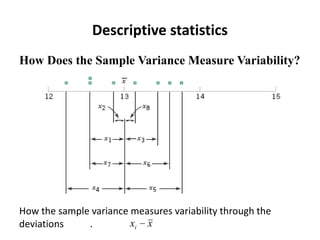
- 13. Definition: Sample VarianceDescriptive statistics
- 14. Descriptive statisticsHow Does the Sample Variance Measure Variability?How the sample variance measures variability through the deviations .
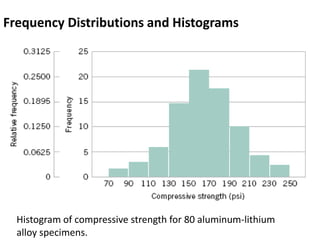
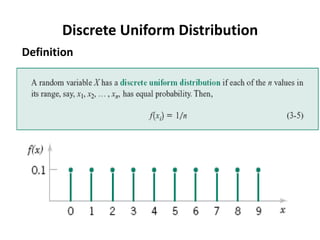
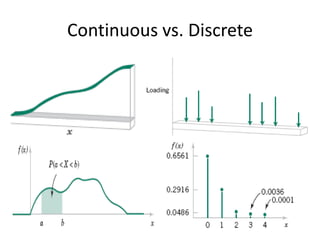
- 17. Frequency Distributions and Histograms A frequency distribution is a more compact summary of data than a stem-and-leaf diagram.
- 18. To construct a frequency distribution, we must divide the range of the data into intervals, which are usually called class intervals, cells, or bins.Constructing a Histogram (Equal Bin Widths):
- 19. Frequency Distributions and Histograms Histogram of compressive strength for 80 aluminum-lithium alloy specimens.
- 21. Stem-and-Leaf Diagrams Data FeaturesWhen an ordered set of data is divided into four equal parts, the division points are called quartiles. The firstor lower quartile, q1, is a value that has approximately one-fourth (25%) of the observations below it and approximately 75% of the observations above. The second quartile, q2, has approximately one-half (50%) of the observations below its value. The second quartile is exactly equal to the median. The thirdor upper quartile, q3, has approximately three-fourths (75%) of the observations below its value. As in the case of the median, the quartiles may not be unique.
- 22. Stem-and-Leaf Diagrams Data FeaturesThe interquartile range is the difference between the upper and lower quartiles, and it is sometimes used as a measure of variability.
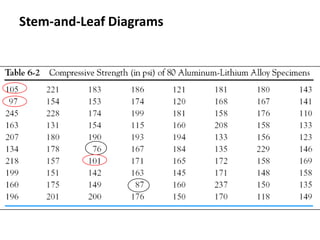
- 23. In general, the 100kth percentile is a data value such that approximately 100k% of the observations are at or below this value and approximately 100(1 - k)% of them are above it.Stem-and-Leaf Diagrams Stem-and-leaf diagram for the compressive strength data
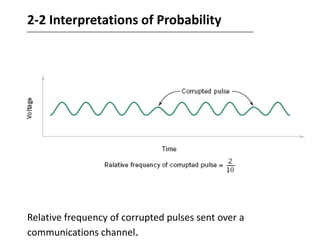
- 24. 2-2 Interpretations of ProbabilityRelative frequency of corrupted pulses sent over a communications channel.
- 25. 2-2 Interpretations of Probability2-2.2 Axioms of Probability
- 26. DistributionProbability distribution of variable x is the description of the probability of each outcome of x.Examples:Tossing a coin, x is getting head, s={0,1} P(x=0)=0.5, P(x=1)=0.5In an experiment of examining 2 independent items from a product line, the probability that an item passes the test is 0.8, if x is the number of products passing the inspection. What is the distribution of x?
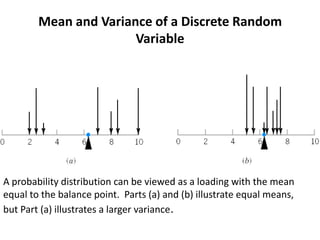
- 27. Mean and Variance of a Discrete Random VariableA probability distribution can be viewed as a loading with the mean equal to the balance point. Parts (a) and (b) illustrate equal means, but Part (a) illustrates a larger variance.
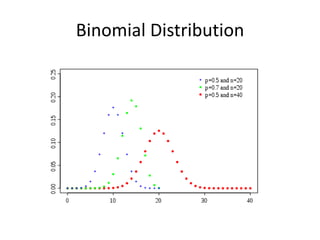
- 29. Binomial DistributionYou know the probability of the outcome of interest in a single try.
- 30. Flip a coin P(H)=1/2
- 31. Draw a card P(K)=4/52
- 32. In a production line P(defective)=0.10
- 33. You repeat the experiment (trial) n times WITH REPLACEMENT
- 34. Flip the coin 7 times
- 35. Draw 5 cards
- 36. (Take an item, test it, return it back) 25 times
- 37. You want to know the probability that you will get a certain outcome x times.
- 38. Probability of getting 3 heads in 7 times knowing that P(H)=0.5
- 39. Probability of getting 5 Kings in 5 drawn cards knowing that P(K)=4/52
- 40. Probability of getting 2 defectives in a sample of 25 items knowing that P(d)=0.1Binomial Distribution
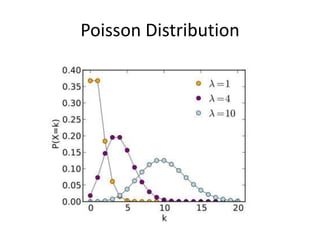
- 41. Poisson DistributionThis distribution deals with the case that you only know THE AVERAGE NUMBER of the required outcomeExamplesFlaws in a rolls of textileCalls to a telephone exchange
- 45. Normal DistributionThe most widely used distributionAlso called Gaussian distributionCan be used to virtually approximate results of any experiment as we will see in later chapters.Characterized by mean and variance.Can you notice it represents weight, height, your strength?
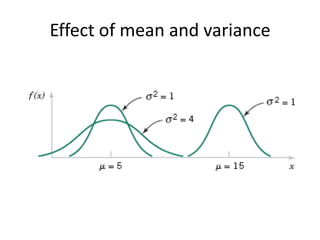
- 46. Effect of mean and variance
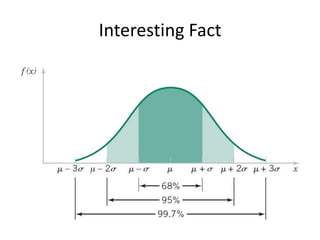
- 47. Interesting Fact
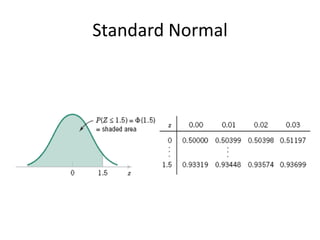
- 48. Standard Normal
- 49. ExampleFind P(Z>1.26)P(Z<-0.86)P(Z>-1.37)P(-1.25<Z<0.37)P(Z<-4.6)Find z such that P(Z>z)=0.05Find z such that P(-z<Z<z)=0.99
- 50. Solution
- 51. ExampleIf the current measurements is a trip of wire are assumed to follow N(10,4).FindProbability that the current will exceed 13 milliamperesProbability that the current will be within 9 to 11 milliamperesThe value for which the probability that the current intensity measurement is below this value is 98%
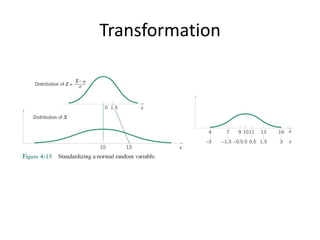
- 52. Transformation
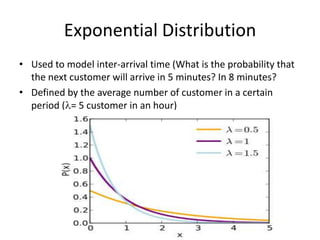
- 53. Exponential DistributionUsed to model inter-arrival time (What is the probability that the next customer will arrive in 5 minutes? In 8 minutes?Defined by the average number of customer in a certain period (= 5 customer in an hour)
- 54. Weibull DistributionThe Weibull distribution is usedIn油reliability engineering油and油failure analysisIn油industrial engineering油to represent油manufacturing油and油delivery油timesIn communications systems engineeringIn radar systems to model the dispersion of the received signals level produced by some types of cluttersIn General insurance to model the size of Reinsurance claimsIn forecasting technological changeIn hydrology the Weibull distribution is applied to extreme events such as annually maximum one-day rainfalls and river discharges. In油weather forecasting
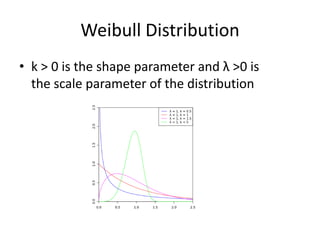
- 55. Weibull Distributionk油> 0 is the油shape parameter油and 了 >0 is the油scale parameter油of the distribution
- 56. Statistical data analysisStudying a problem through the use of statistical data analysis usually involves four basic steps.Defining the problemCollecting the data油Analyzing the data油Reporting the results
- 57. Collecting the dataTwo important aspects of a statistical study are:油Population - a set of all the elements of interest in a studySample - a subset of the population油statistical inference is to obtain information about a population form information contained in a sampleCross-sectional data re data collected at the same or approximately the same point in time. Time series data are data collected over several time periods.
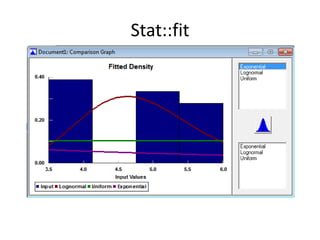
- 58. Analyzing the dataHypothesis test: Claim that a collected data can be approximated by a certain distributionIf we find a significant evidence that this is not true, we reject the claim
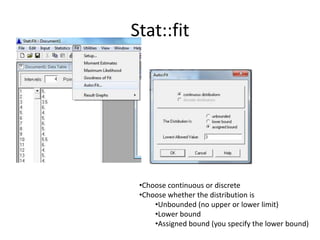
- 59. Stat::fitChoose file-open then choose files of type data files (*.txt)Or Insert the data here
- 60. Stat::fitChoose continuous or discrete
- 61. Choose whether the distribution is
- 62. Unbounded (no upper or lower limit)
- 63. Lower bound
- 64. Assigned bound (you specify the lower bound)Stat::fitChoose assigned bound and specify the lower bound as 0.
- 65. Stat::fit