TRApezoids
Download as PPTX, PDF0 likes11 views
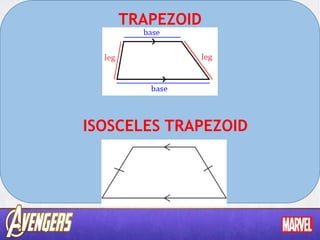
This document discusses properties of trapezoids and isosceles trapezoids. It defines a trapezoid as a quadrilateral with one pair of parallel opposite sides. An isosceles trapezoid is a trapezoid where the two non-parallel sides, or legs, are congruent. The document includes examples of identifying trapezoids and isosceles trapezoids based on side lengths and slopes. It also defines the median of a trapezoid as the segment joining the midpoints of the legs. Theorems and examples are provided about angles and properties of trapezoids. Review and practice questions are listed at the end.
1 of 13
Download to read offline






Recommended
Kostadin Trencevski - Noncommutative Coordinates and Applications



Kostadin Trencevski - Noncommutative Coordinates and ApplicationsSEENET-MTP
Ã˝
Lecture by Prof. Dr Kostadin Trenčevski (Institute of Mathematics, Saint Cyril and Methodius University, Skopje, FYR Macedonia.) on October 27, 2010 at the Faculty of Science and Mathematics, Nis, Serbia.Fundamental Of Physics Measurement



Fundamental Of Physics MeasurementMuhammad Faizan Musa
Ã˝
After reading this module, you should be able to . . .
1.01 Identify the base quantities in the SI system.
1.02 Name the most frequently used prefixes for
SI units.
1.03 Change units (here for length, area, and volume) by
using chain-link conversions.
1.04 Explain that the meter is defined in terms of the speed of
light in vacuum.Fundamentals of Physics "MOTION IN TWO AND THREE DIMENSIONS"



Fundamentals of Physics "MOTION IN TWO AND THREE DIMENSIONS"Muhammad Faizan Musa
Ã˝
4-1 POSITION AND DISPLACEMENT
After reading this module, you should be able to . . .
4.01 Draw two-dimensional and three-dimensional position
vectors for a particle, indicating the components along the
axes of a coordinate system.
4.02 On a coordinate system, determine the direction and
magnitude of a particle’s position vector from its components, and vice versa.
4.03 Apply the relationship between a particle’s displacement vector and its initial and final position vectors.
4-2 AVERAGE VELOCITY AND INSTANTANEOUS VELOCITY
After reading this module, you should be able to . . .
4.04 Identify that velocity is a vector quantity and thus has
both magnitude and direction and also has components.
4.05 Draw two-dimensional and three-dimensional velocity
vectors for a particle, indicating the components along the
axes of the coordinate system.
4.06 In magnitude-angle and unit-vector notations, relate a particle’s initial and final position vectors, the time interval between
those positions, and the particle’s average velocity vector.
4.07 Given a particle’s position vector as a function of time,
determine its (instantaneous) velocity vector. etc...Learning object 1 physics 101



Learning object 1 physics 101Alykhan Devsi
Ã˝
This document discusses the displacement function of a pulse traveling through a medium and how it can be used to determine the velocity of the medium. It provides an example displacement function D(x,t) = 2/(x-vt)4+3 and explains that the sign of the term vt indicates the direction of pulse movement. It then gives an example problem asking the reader to determine the velocity of a pulse with displacement function D(x,t) = 5/(x-0.7t)2+3 and the speeds of string elements at specific positions and times using the derivative of the displacement function.258418024 xi physics



258418024 xi physicshimanshuyadavhimanshu
Ã˝
This document contains a 30 question sample physics exam for Class 11 in India. The questions cover a range of topics including centripetal force, work, projectile motion, vectors, friction, Newton's laws of motion, and conservation of energy. The exam is 3 hours long and has a maximum score of 70 marks. It was submitted by Vinod Kumar Indora and contains their contact information at the end.Fundamentals of Physics (MOTION ALONG A STRAIGHT LINE)



Fundamentals of Physics (MOTION ALONG A STRAIGHT LINE)Muhammad Faizan Musa
Ã˝
2-1 POSITION, DISPLACEMENT, AND AVERAGE VELOCITY
After reading this module, you should be able to …
2.01 Identify that if all parts of an object move in the same direction and at the same rate, we can treat the object as if it
were a (point-like) particle. (This chapter is about the motion of such objects.)
2.02 Identify that the position of a particle is its location as
read on a scaled axis, such as an x-axis.
2.03 Apply the relationship between a particle’s
displacement and its initial and final positions.
2.04 Apply the relationship between a particle’s average
velocity, its displacement, and the time interval for that
displacement.
2.05 Apply the relationship between a particle’s average
speed, the total distance it moves, and the time interval for
the motion.
2.06 Given a graph of a particle’s position versus time,
determine the average velocity between any two particular
times.
2-1 POSITION, DISPLACEMENT, AND AVERAGE VELOCITY
After reading this module, you should be able to . . .
2.07 Given a particle’s position as a function of time,
calculate the instantaneous velocity for any particular time.
2.08 Given a graph of a particle’s position versus time, determine the instantaneous velocity for any particular time.
2.09 Identify speed as the magnitude of the instantaneous
velocity.
etc......Fundamentals of Physics "VECTORS"



Fundamentals of Physics "VECTORS"Muhammad Faizan Musa
Ã˝
3-1 VECTORS AND THEIR COMPONENTS
After reading this module, you should be able to . . .
3.01 Add vectors by drawing them in head-to-tail arrangements, applying the commutative and associative laws.
3.02 Subtract a vector from a second one.
3.03 Calculate the components of a vector on a given coordinate system, showing them in a drawing.
3.04 Given the components of a vector, draw the vector
and determine its magnitude and orientation.
3.05 Convert angle measures between degrees and radians.
3-2 UNIT VECTORS, ADDING VECTORS BY COMPONENTS
After reading this module, you should be able to . . .
3.06 Convert a vector between magnitude-angle and unit vector notations.
3.07 Add and subtract vectors in magnitude-angle notation
and in unit-vector notation.
3.08 Identify that, for a given vector, rotating the coordinate
system about the origin can change the vector’s components but not the vector itself.
etc...Learning object 1 physics 101



Learning object 1 physics 101Alykhan Devsi
Ã˝
This document discusses displacement functions that describe pulses moving through a medium. It begins by explaining how a displacement function represents the position of each element in the medium at a fixed time. An example displacement function is given. A warmup question asks the reader to identify which of three equations describes a pulse moving in the decreasing x direction. The correct answer, B, is explained by comparing addition and subtraction in the displacement functions. Another example calculates the velocity of a pulse from its displacement function and finds the speeds of elements at two positions and a time. In summary, the document covers using displacement functions to determine a pulse's velocity and the speeds of medium elements at given points.Applications of differential equation



Applications of differential equationDeekshaSrivas
Ã˝
1. The document discusses differential equations and their applications. It defines differential equations and describes their use in fields like physics, engineering, biology and economics to model complex systems.
2. Examples of first order differential equations are given to model exponential growth, exponential decay, and an RL circuit. Higher order differential equations are used to model falling objects and Newton's law of cooling.
3. The key applications covered are population growth, radioactive decay, free falling objects, heat transfer, and electric circuits. Solving the differential equations gives mathematical models relating variables like position, temperature, and current over time.Physmed11 u1 1



Physmed11 u1 1Dr. Hazem Falah Sakeek
Ã˝
This document provides an overview of a physics lecture on units, dimensions, and vectors. The lecture introduces students to the International System of Units (SI) and the metric system of measurement. It discusses the basic SI units of length, mass, and time. The lecture also covers dimensional analysis, which uses the dimensions of physical quantities to check the validity of equations. Vector concepts such as coordinate systems and vector components are also introduced. The document aims to equip medical sciences students with the fundamental physics concepts needed to understand measurements and quantitative relationships in physics.Motion notes by R K Chaudhari sir



Motion notes by R K Chaudhari sirraghvendra0123
Ã˝
This document discusses key concepts related to motion including reference frames, distance and displacement, speed and velocity, uniform and non-uniform motion, and equations of motion. It defines scalar and vector quantities, explains the difference between distance and displacement, defines average speed and velocity. It also describes motion graphs including distance-time and velocity-time graphs, and how to derive the equations of motion using graphical methods. Finally, it discusses uniform circular motion and how velocity changes direction while speed remains constant.XI session ending exam 2013 14



XI session ending exam 2013 14KV no 1 AFS Jodhpur raj.
Ã˝
This document appears to be an examination for a Physics class covering various topics:
1) It contains 20 multi-part physics problems testing concepts like kinematics, forces, energy, momentum, properties of matter, heat, sound, and optics.
2) The problems cover the calculation of values like percentage error, rounding numbers, work, pressure, velocity, temperature changes, frequencies, trajectories, moments of inertia, Bernoulli's theorem, and fluid flow rates.
3) The document tests the student's understanding and ability to apply physics formulas to different scenarios and situations.Chapter 1(3)DIMENSIONAL ANALYSIS



Chapter 1(3)DIMENSIONAL ANALYSISFIKRI RABIATUL ADAWIAH
Ã˝
This document discusses dimensional analysis and its applications. It can be used to:
1) Derive equations by ensuring the dimensions on both sides are equal
2) Check if equations are dimensionally correct
3) Find the dimensions/units of derived quantities
Examples are provided to illustrate deriving equations based on quantities' dimensions and checking the homogeneity of equations.International Journal of Engineering Research and Development (IJERD)



International Journal of Engineering Research and Development (IJERD)IJERD Editor
Ã˝
journal publishing, how to publish research paper, Call For research paper, international journal, publishing a paper, IJERD, journal of science and technology, how to get a research paper published, publishing a paper, publishing of journal, publishing of research paper, reserach and review articles, IJERD Journal, How to publish your research paper, publish research paper, open access engineering journal, Engineering journal, Mathemetics journal, Physics journal, Chemistry journal, Computer Engineering, Computer Science journal, how to submit your paper, peer reviw journal, indexed journal, reserach and review articles, engineering journal, www.ijerd.com, research journals,
yahoo journals, bing journals, International Journal of Engineering Research and Development, google journals, hard copy of journalMiao



MiaoPalaniswamy Sankariah
Ã˝
This document provides an outline of string theory. It begins with background on reductionism in physics and the unification of forces. String theory emerged as a way to address difficulties in quantizing gravity. There are five consistent string theories in 10 dimensions: type I open superstring theory with oriented strings; type IIA closed superstring theory with two independent sets of supersymmetry; heterotic string theories that combine bosonic and supersymmetric strings. String theory led to the discovery of supersymmetry and relates fundamental forces and particles to vibrational modes of strings.Applications of differential equation in Physics and Biology



Applications of differential equation in Physics and BiologyAhamed Yoonus S
Ã˝
This document discusses several applications of differential equations in physics. It provides examples of how differential equations are used to model radioactive decay, linear and projectile motion, harmonic oscillations, and more. Solving these differential equations provides insights into the physical processes being modeled and has allowed technological progress across many scientific disciplines. Differential equations are necessary to describe most physical phenomena accurately because real-world relationships are typically non-linear rather than linear.Dimensions and Dimensional Analysis



Dimensions and Dimensional AnalysisTanzania Atomic Energy Commission
Ã˝
Dimensional analysis offers a method for reducing complex physical problems to the simplest (that is, most economical) form prior to obtaining a quantitative answer. Coordinate systems



Coordinate systemsAmeenSoomro1
Ã˝
1) The document provides an overview of classical mechanics, including definitions of key concepts like space, time, mass, and force. It summarizes Newton's three laws of motion and how they relate to concepts like momentum and inertia.
2) Key principles of classical mechanics are explained, such as reference frames, Newton's laws, and conservation of momentum. Vector operations and products are also defined.
3) Examples are given to illustrate fundamental principles, like Newton's third law and how it relates to conservation of momentum in systems with multiple objects. Coordinate systems are briefly introduced.Second application of dimensional analysis



Second application of dimensional analysisJaypee Institute of Information Technology
Ã˝
Second application of dimensional analysis
If you liked it don't forget to follow me-
Instagram-yadavgaurav251
Facebook-www.facebook.com/yadavgaurav251 Sistema internacional de unidades (EPITyC)



Sistema internacional de unidades (EPITyC)Yimmy HZ
Ã˝
The document discusses the International System of Units (SI). It states that the SI is the heir to the old metric decimal system, so it is also known generically as the metric system. One of the main characteristics of the International System of Units is that its units are based on fundamental physical phenomena. The units of the SI are the international reference for indications of all measuring instruments. [/SUMMARY]Lecture 1 kosygin



Lecture 1 kosyginKosygin Leishangthem
Ã˝
The document discusses key concepts in mechanics including:
- Mechanics deals with the motion and equilibrium of bodies under forces.
- Statics analyzes equilibrium of rigid bodies at rest, while dynamics analyzes bodies in motion.
- Basic terms like length, area, volume, force, mass, and weight are introduced.
- Concepts like space, time, mass, particles, and forces are defined.
- Coordinate systems including Cartesian, cylindrical and spherical are described to specify positions.
- Newton's laws of motion and gravitational attraction form the basis of mechanics analyses.G11ex1



G11ex1alvarballon
Ã˝
1. The document contains exercises on physics concepts related to kinematics including derivations of equations for displacement, velocity, and acceleration for objects moving with constant velocity in one dimension.
2. Review problems ask the reader to calculate displacements and velocities using kinematic equations and graphs of position, velocity, and acceleration versus time.
3. Additional problems relate to Newton's law of universal gravitation, calculating gravitational field strengths and accelerations near spherical objects like stars and planets.Xi session ending exam 2010 11



Xi session ending exam 2010 11KV no 1 AFS Jodhpur raj.
Ã˝
This document contains instructions and questions for a physics exam for Class XI. It is 3 pages long and has a total of 30 questions worth 70 marks. Questions 1-8 are 1 mark each, questions 9-18 are 2 marks each, questions 19-27 are 3 marks each, and questions 28-30 are 5 marks each. The exam covers topics in physics including motion, forces, work, energy, gravitation, properties of matter, heat and thermodynamics, oscillations and waves. Students are provided with relevant physical constants and formulas. They are not permitted to use calculators during the exam.Chapter 1 units,physicalquantities and vectors



Chapter 1 units,physicalquantities and vectorsPaouloDe
Ã˝
This document provides an overview of fundamental concepts in physics including units, quantities, vectors, and systems of units. It discusses scalar and vector quantities, and how vectors can be represented graphically or through their components. Methods for adding and subtracting vectors using graphical and analytical approaches like trigonometry and components are presented. Fundamental quantities like length, mass and time that other derived quantities are based on are defined. Common systems of units including SI, CGS and English units are compared.C1h2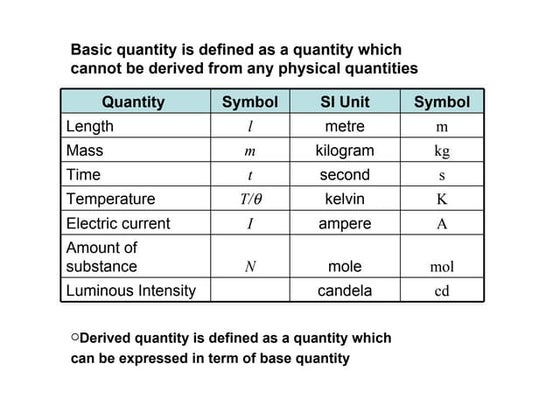



C1h2azlirozita
Ã˝
The document discusses dimensional analysis, which is a technique used to express physical quantities in terms of base quantities. It defines basic and derived quantities, and lists common base quantities like length, mass, and time. The document also shows how to use dimensional analysis to determine the units and dimensional consistency of equations. Examples are provided to illustrate determining units, checking if equations are dimensionally correct, and deriving relationships between physical quantities.The phase plane of moving discrete breathers



The phase plane of moving discrete breathersPaul Houle
Ã˝
1. The document studies discrete breathers in a periodic chain of 5 atoms coupled by quadratic-quartic springs. It uses discrete symmetries to simplify the analysis and visualize the phase space.
2. It finds that unlike even atom chains, odd atom chains have no energy threshold for breathers due to degenerate band edge modes. It observes long-lived "hopping breathers" that move chaotically in the separatrix region dividing pinned and moving states.
3. It applies linear stability analysis to measure quasi-phonon frequencies around breathers and map the stable and unstable manifolds of unstable breathers. This allows systematically launching moving or pinned breathers by perturbing stable or unstable breathers.MEKANIKA Bab 1-pusat-massa1



MEKANIKA Bab 1-pusat-massa1Fathur Rozaq
Ã˝
This document discusses calculating the centers of mass of various objects. It begins by defining center of mass, center of gravity, and centroid. It then provides formulas and examples for calculating the centers of mass of plane areas and curves using calculus, whether the equations are in x-y or polar coordinates. It also discusses centers of mass for three-dimensional objects and the physical significance of calculating centers of mass, such as for analyzing mechanical systems in static equilibrium or dynamics. The overall purpose is to introduce methods for determining the positions of centers of mass through calculation.Lecture19



Lecture19nomio0703
Ã˝
The document discusses the results of an exam in a physics class on elasticity and oscillations. It provides the grade distributions and averages for the exam, along with lecture materials on springs, Hooke's law, simple harmonic motion, and examples of physics problems involving springs and oscillations. Key concepts covered include restoring forces, potential energy in springs, Young's modulus, and the equations of motion for simple harmonic oscillators.6 3 Proving Parallelograms



6 3 Proving Parallelogramslmrogers03
Ã˝
This document discusses different ways to prove that a quadrilateral is a parallelogram, including: if both pairs of opposite sides are congruent; if an angle is supplementary to its consecutive angles; if both pairs of opposite angles are congruent; if the diagonals of a quadrilateral bisect each other; or if one pair of opposite sides is both congruent and parallel. It provides examples of each theorem and assigns practice problems for students to complete.Trapezoid-and-Isosceles-Trapezoid-Theorems-6-9-1 (1).pdf



Trapezoid-and-Isosceles-Trapezoid-Theorems-6-9-1 (1).pdfCristhelMacajeto2
Ã˝
- A trapezoid is a quadrilateral with one pair of parallel sides called the bases. The non-parallel sides are called the legs.
- An isosceles trapezoid has one pair of parallel sides and one pair of congruent non-parallel sides called legs.
- Theorems about the isosceles trapezoid include: the base angles are congruent, opposite angles are supplementary, and the diagonals are congruent.
- The median of any trapezoid is parallel to the bases and is equal to half the sum of the bases.More Related Content
What's hot (20)
Applications of differential equation



Applications of differential equationDeekshaSrivas
Ã˝
1. The document discusses differential equations and their applications. It defines differential equations and describes their use in fields like physics, engineering, biology and economics to model complex systems.
2. Examples of first order differential equations are given to model exponential growth, exponential decay, and an RL circuit. Higher order differential equations are used to model falling objects and Newton's law of cooling.
3. The key applications covered are population growth, radioactive decay, free falling objects, heat transfer, and electric circuits. Solving the differential equations gives mathematical models relating variables like position, temperature, and current over time.Physmed11 u1 1



Physmed11 u1 1Dr. Hazem Falah Sakeek
Ã˝
This document provides an overview of a physics lecture on units, dimensions, and vectors. The lecture introduces students to the International System of Units (SI) and the metric system of measurement. It discusses the basic SI units of length, mass, and time. The lecture also covers dimensional analysis, which uses the dimensions of physical quantities to check the validity of equations. Vector concepts such as coordinate systems and vector components are also introduced. The document aims to equip medical sciences students with the fundamental physics concepts needed to understand measurements and quantitative relationships in physics.Motion notes by R K Chaudhari sir



Motion notes by R K Chaudhari sirraghvendra0123
Ã˝
This document discusses key concepts related to motion including reference frames, distance and displacement, speed and velocity, uniform and non-uniform motion, and equations of motion. It defines scalar and vector quantities, explains the difference between distance and displacement, defines average speed and velocity. It also describes motion graphs including distance-time and velocity-time graphs, and how to derive the equations of motion using graphical methods. Finally, it discusses uniform circular motion and how velocity changes direction while speed remains constant.XI session ending exam 2013 14



XI session ending exam 2013 14KV no 1 AFS Jodhpur raj.
Ã˝
This document appears to be an examination for a Physics class covering various topics:
1) It contains 20 multi-part physics problems testing concepts like kinematics, forces, energy, momentum, properties of matter, heat, sound, and optics.
2) The problems cover the calculation of values like percentage error, rounding numbers, work, pressure, velocity, temperature changes, frequencies, trajectories, moments of inertia, Bernoulli's theorem, and fluid flow rates.
3) The document tests the student's understanding and ability to apply physics formulas to different scenarios and situations.Chapter 1(3)DIMENSIONAL ANALYSIS



Chapter 1(3)DIMENSIONAL ANALYSISFIKRI RABIATUL ADAWIAH
Ã˝
This document discusses dimensional analysis and its applications. It can be used to:
1) Derive equations by ensuring the dimensions on both sides are equal
2) Check if equations are dimensionally correct
3) Find the dimensions/units of derived quantities
Examples are provided to illustrate deriving equations based on quantities' dimensions and checking the homogeneity of equations.International Journal of Engineering Research and Development (IJERD)



International Journal of Engineering Research and Development (IJERD)IJERD Editor
Ã˝
journal publishing, how to publish research paper, Call For research paper, international journal, publishing a paper, IJERD, journal of science and technology, how to get a research paper published, publishing a paper, publishing of journal, publishing of research paper, reserach and review articles, IJERD Journal, How to publish your research paper, publish research paper, open access engineering journal, Engineering journal, Mathemetics journal, Physics journal, Chemistry journal, Computer Engineering, Computer Science journal, how to submit your paper, peer reviw journal, indexed journal, reserach and review articles, engineering journal, www.ijerd.com, research journals,
yahoo journals, bing journals, International Journal of Engineering Research and Development, google journals, hard copy of journalMiao



MiaoPalaniswamy Sankariah
Ã˝
This document provides an outline of string theory. It begins with background on reductionism in physics and the unification of forces. String theory emerged as a way to address difficulties in quantizing gravity. There are five consistent string theories in 10 dimensions: type I open superstring theory with oriented strings; type IIA closed superstring theory with two independent sets of supersymmetry; heterotic string theories that combine bosonic and supersymmetric strings. String theory led to the discovery of supersymmetry and relates fundamental forces and particles to vibrational modes of strings.Applications of differential equation in Physics and Biology



Applications of differential equation in Physics and BiologyAhamed Yoonus S
Ã˝
This document discusses several applications of differential equations in physics. It provides examples of how differential equations are used to model radioactive decay, linear and projectile motion, harmonic oscillations, and more. Solving these differential equations provides insights into the physical processes being modeled and has allowed technological progress across many scientific disciplines. Differential equations are necessary to describe most physical phenomena accurately because real-world relationships are typically non-linear rather than linear.Dimensions and Dimensional Analysis



Dimensions and Dimensional AnalysisTanzania Atomic Energy Commission
Ã˝
Dimensional analysis offers a method for reducing complex physical problems to the simplest (that is, most economical) form prior to obtaining a quantitative answer. Coordinate systems



Coordinate systemsAmeenSoomro1
Ã˝
1) The document provides an overview of classical mechanics, including definitions of key concepts like space, time, mass, and force. It summarizes Newton's three laws of motion and how they relate to concepts like momentum and inertia.
2) Key principles of classical mechanics are explained, such as reference frames, Newton's laws, and conservation of momentum. Vector operations and products are also defined.
3) Examples are given to illustrate fundamental principles, like Newton's third law and how it relates to conservation of momentum in systems with multiple objects. Coordinate systems are briefly introduced.Second application of dimensional analysis



Second application of dimensional analysisJaypee Institute of Information Technology
Ã˝
Second application of dimensional analysis
If you liked it don't forget to follow me-
Instagram-yadavgaurav251
Facebook-www.facebook.com/yadavgaurav251 Sistema internacional de unidades (EPITyC)



Sistema internacional de unidades (EPITyC)Yimmy HZ
Ã˝
The document discusses the International System of Units (SI). It states that the SI is the heir to the old metric decimal system, so it is also known generically as the metric system. One of the main characteristics of the International System of Units is that its units are based on fundamental physical phenomena. The units of the SI are the international reference for indications of all measuring instruments. [/SUMMARY]Lecture 1 kosygin



Lecture 1 kosyginKosygin Leishangthem
Ã˝
The document discusses key concepts in mechanics including:
- Mechanics deals with the motion and equilibrium of bodies under forces.
- Statics analyzes equilibrium of rigid bodies at rest, while dynamics analyzes bodies in motion.
- Basic terms like length, area, volume, force, mass, and weight are introduced.
- Concepts like space, time, mass, particles, and forces are defined.
- Coordinate systems including Cartesian, cylindrical and spherical are described to specify positions.
- Newton's laws of motion and gravitational attraction form the basis of mechanics analyses.G11ex1



G11ex1alvarballon
Ã˝
1. The document contains exercises on physics concepts related to kinematics including derivations of equations for displacement, velocity, and acceleration for objects moving with constant velocity in one dimension.
2. Review problems ask the reader to calculate displacements and velocities using kinematic equations and graphs of position, velocity, and acceleration versus time.
3. Additional problems relate to Newton's law of universal gravitation, calculating gravitational field strengths and accelerations near spherical objects like stars and planets.Xi session ending exam 2010 11



Xi session ending exam 2010 11KV no 1 AFS Jodhpur raj.
Ã˝
This document contains instructions and questions for a physics exam for Class XI. It is 3 pages long and has a total of 30 questions worth 70 marks. Questions 1-8 are 1 mark each, questions 9-18 are 2 marks each, questions 19-27 are 3 marks each, and questions 28-30 are 5 marks each. The exam covers topics in physics including motion, forces, work, energy, gravitation, properties of matter, heat and thermodynamics, oscillations and waves. Students are provided with relevant physical constants and formulas. They are not permitted to use calculators during the exam.Chapter 1 units,physicalquantities and vectors



Chapter 1 units,physicalquantities and vectorsPaouloDe
Ã˝
This document provides an overview of fundamental concepts in physics including units, quantities, vectors, and systems of units. It discusses scalar and vector quantities, and how vectors can be represented graphically or through their components. Methods for adding and subtracting vectors using graphical and analytical approaches like trigonometry and components are presented. Fundamental quantities like length, mass and time that other derived quantities are based on are defined. Common systems of units including SI, CGS and English units are compared.C1h2



C1h2azlirozita
Ã˝
The document discusses dimensional analysis, which is a technique used to express physical quantities in terms of base quantities. It defines basic and derived quantities, and lists common base quantities like length, mass, and time. The document also shows how to use dimensional analysis to determine the units and dimensional consistency of equations. Examples are provided to illustrate determining units, checking if equations are dimensionally correct, and deriving relationships between physical quantities.The phase plane of moving discrete breathers



The phase plane of moving discrete breathersPaul Houle
Ã˝
1. The document studies discrete breathers in a periodic chain of 5 atoms coupled by quadratic-quartic springs. It uses discrete symmetries to simplify the analysis and visualize the phase space.
2. It finds that unlike even atom chains, odd atom chains have no energy threshold for breathers due to degenerate band edge modes. It observes long-lived "hopping breathers" that move chaotically in the separatrix region dividing pinned and moving states.
3. It applies linear stability analysis to measure quasi-phonon frequencies around breathers and map the stable and unstable manifolds of unstable breathers. This allows systematically launching moving or pinned breathers by perturbing stable or unstable breathers.MEKANIKA Bab 1-pusat-massa1



MEKANIKA Bab 1-pusat-massa1Fathur Rozaq
Ã˝
This document discusses calculating the centers of mass of various objects. It begins by defining center of mass, center of gravity, and centroid. It then provides formulas and examples for calculating the centers of mass of plane areas and curves using calculus, whether the equations are in x-y or polar coordinates. It also discusses centers of mass for three-dimensional objects and the physical significance of calculating centers of mass, such as for analyzing mechanical systems in static equilibrium or dynamics. The overall purpose is to introduce methods for determining the positions of centers of mass through calculation.Lecture19



Lecture19nomio0703
Ã˝
The document discusses the results of an exam in a physics class on elasticity and oscillations. It provides the grade distributions and averages for the exam, along with lecture materials on springs, Hooke's law, simple harmonic motion, and examples of physics problems involving springs and oscillations. Key concepts covered include restoring forces, potential energy in springs, Young's modulus, and the equations of motion for simple harmonic oscillators.Similar to TRApezoids (20)
6 3 Proving Parallelograms



6 3 Proving Parallelogramslmrogers03
Ã˝
This document discusses different ways to prove that a quadrilateral is a parallelogram, including: if both pairs of opposite sides are congruent; if an angle is supplementary to its consecutive angles; if both pairs of opposite angles are congruent; if the diagonals of a quadrilateral bisect each other; or if one pair of opposite sides is both congruent and parallel. It provides examples of each theorem and assigns practice problems for students to complete.Trapezoid-and-Isosceles-Trapezoid-Theorems-6-9-1 (1).pdf



Trapezoid-and-Isosceles-Trapezoid-Theorems-6-9-1 (1).pdfCristhelMacajeto2
Ã˝
- A trapezoid is a quadrilateral with one pair of parallel sides called the bases. The non-parallel sides are called the legs.
- An isosceles trapezoid has one pair of parallel sides and one pair of congruent non-parallel sides called legs.
- Theorems about the isosceles trapezoid include: the base angles are congruent, opposite angles are supplementary, and the diagonals are congruent.
- The median of any trapezoid is parallel to the bases and is equal to half the sum of the bases.2.8.4 Kites and Trapezoids



2.8.4 Kites and Trapezoidssmiller5
Ã˝
This document discusses properties of kites and trapezoids. It defines kites as quadrilaterals with two pairs of congruent consecutive nonparallel sides, and notes their diagonals are perpendicular. It defines trapezoids as quadrilaterals with one pair of parallel sides called bases, and notes angles along the legs are supplementary. It provides theorems about isosceles trapezoids having congruent base angles or congruent diagonals. It also states the midsegment theorem for trapezoids.2.7.5 Kites and Trapezoids



2.7.5 Kites and Trapezoidssmiller5
Ã˝
This document defines and provides properties of kites and trapezoids. It states that a kite is a quadrilateral with two pairs of congruent consecutive sides, and its diagonals are perpendicular. A trapezoid has one pair of parallel sides called bases, and the nonparallel sides are legs. An isosceles trapezoid has two congruent base angles. The midsegment of a trapezoid is parallel to the bases and is half the sum of the base lengths. Examples are provided to demonstrate solving problems using properties of kites and trapezoids.TRIANGLE-MIDLINE-THEOREM-TRAPEZOID-KITE.pdf



TRIANGLE-MIDLINE-THEOREM-TRAPEZOID-KITE.pdfTreshaBahandi
Ã˝
1. The document provides definitions and theorems related to geometric shapes including triangles, trapezoids, kites, and parallelograms. It defines key terms like midline, median, diagonal, and congruent sides.
2. Theorems covered include the triangle midline theorem stating the midline is parallel to the third side and half its length. For trapezoids, the midsegment theorem states the median is parallel to the bases and half their sum.
3. Theorems for kites include the diagonals being perpendicular and one diagonal bisecting the other or bisecting a pair of opposite angles.2.8.5 Kites and Trapezoids



2.8.5 Kites and Trapezoidssmiller5
Ã˝
This document discusses properties of kites and trapezoids. It defines kites as quadrilaterals with two pairs of congruent consecutive sides and states properties of kites including perpendicular diagonals and one pair of opposite congruent angles. It also defines trapezoids as quadrilaterals with one pair of parallel sides, called bases, and discusses isosceles trapezoids. Theorems are presented about base angles and diagonals of isosceles trapezoids. The midsegment theorem for trapezoids states the midsegment is parallel to the bases and its length is half the sum of the base lengths. Examples apply the properties and theorems to solve problems.Geometry Section 6-6



Geometry Section 6-6Jimbo Lamb
Ã˝
The document defines key terms and theorems related to trapezoids and kites. It provides definitions for trapezoid, bases, legs of a trapezoid, base angles, isosceles trapezoid, midsegment of a trapezoid, and kite. It also lists theorems about properties of isosceles trapezoids and kites. Two examples problems are included, one finding measures of an isosceles trapezoid and another showing a quadrilateral is a trapezoid.Obj. 28 Kites and Trapezoids



Obj. 28 Kites and Trapezoidssmiller5
Ã˝
1) The document discusses properties of kites and trapezoids, including that kites have perpendicular diagonals and one pair of congruent opposite angles, and trapezoids have one pair of parallel sides called bases.
2) It provides theorems about isosceles trapezoids, including that each pair of base angles is congruent if it is isosceles.
3) The trapezoid midsegment theorem states that the midsegment of a trapezoid is parallel to the bases and its length is half the sum of the base lengths.Geometry unit 6.2.2



Geometry unit 6.2.2Mark Ryder
Ã˝
This document discusses proving that quadrilaterals are parallelograms using various theorems and properties of parallelograms. It provides examples of showing quadrilateral figures are parallelograms by proving pairs of opposite sides are parallel, pairs of angles are supplementary, or the diagonals of the figure bisect each other. The document also discusses determining if given information is sufficient to classify a quadrilateral as a parallelogram and applying properties of parallelograms to real world examples.6.5 Trapezoids and Kites.ppt



6.5 Trapezoids and Kites.pptRizaCatli2
Ã˝
This document discusses properties of trapezoids and kites. It defines a trapezoid as a quadrilateral with one pair of parallel sides, and an isosceles trapezoid as having congruent legs. Theorems state that in an isosceles trapezoid, the base angles are congruent and the diagonals are congruent. A midsegment connects the midpoints of the legs and equals half the sum of the parallel sides. A kite has two pairs of congruent adjacent sides, with perpendicular diagonals and one pair of congruent opposite angles. The document provides homework problems related to these shapes.6.5 Trapezoids and Kites.ppt



6.5 Trapezoids and Kites.pptssuser209495
Ã˝
This document discusses properties of trapezoids and kites. It defines a trapezoid as a quadrilateral with one pair of parallel sides, and an isosceles trapezoid as having congruent legs. Theorems state that in an isosceles trapezoid, the base angles are congruent and the diagonals are congruent. A midsegment connects the midpoints of the legs and equals half the sum of the parallel sides. A kite has two distinct pairs of congruent adjacent sides, with perpendicular diagonals and one pair of opposite angles that are congruent. The document provides homework problems related to these shapes.Corpo rigido



Corpo rigidoelysioruggeri
Ã˝
1) The motion of a rigid body can be described by tracking the position of a reference trihedron attached to the body over time.
2) At each instant, the orientation of the mobile trihedron relative to a fixed reference frame is defined by a rotation dyadic with a rotation axis and angle.
3) The rotation dyadic transforms the fixed frame vectors into the mobile frame vectors, allowing the position and orientation of any point on the rigid body to be determined as a function of time.Geometry Section 6-3



Geometry Section 6-3Jimbo Lamb
Ã˝
The document discusses properties of parallelograms and provides examples of determining if a quadrilateral is a parallelogram. It defines four theorems for identifying parallelograms based on opposite sides, opposite angles, bisecting diagonals, and parallel/congruent sides. Examples solve systems of equations to find values of variables such that the quadrilaterals satisfy parallelogram properties. One example uses slopes of side segments to show a quadrilateral is a parallelogram due to parallel opposite sides.Adv math[unit 4]![Adv math[unit 4]](https://cdn.slidesharecdn.com/ss_thumbnails/advmathunit4-140731091744-phpapp01-thumbnail.jpg?width=560&fit=bounds)
![Adv math[unit 4]](https://cdn.slidesharecdn.com/ss_thumbnails/advmathunit4-140731091744-phpapp01-thumbnail.jpg?width=560&fit=bounds)
![Adv math[unit 4]](https://cdn.slidesharecdn.com/ss_thumbnails/advmathunit4-140731091744-phpapp01-thumbnail.jpg?width=560&fit=bounds)
![Adv math[unit 4]](https://cdn.slidesharecdn.com/ss_thumbnails/advmathunit4-140731091744-phpapp01-thumbnail.jpg?width=560&fit=bounds)
Adv math[unit 4]Nald Torres
Ã˝
This document discusses power series and power series solutions of differential equations. It begins by defining sequences and series, and discussing concepts such as convergence, divergence, and limits. It then introduces power series and examples of testing series for convergence using tests like the ratio test, root test, and integral test. It provides examples of determining if alternating series converge absolutely or conditionally. In summary, the document covers fundamental concepts of sequences and series, introduces power series, and discusses various tests for determining convergence of series.Module5 dodong2



Module5 dodong2Dods Dodong
Ã˝
This document provides instruction and content for a Grade 9 mathematics module on parallelograms. It includes definitions of parallelograms and their properties. Several theorems are proved, including those regarding parallelograms, rectangles, rhombuses, the midline theorem, trapezoids, and kites. Example problems are also provided to demonstrate applying the properties and theorems of parallelograms.5 2 Prove quadrilaterals are parallelograms



5 2 Prove quadrilaterals are parallelogramslmrogers03
Ã˝
This document discusses five ways to prove that a quadrilateral is a parallelogram:
1. By showing that both pairs of opposite sides are parallel.
2. By showing that both pairs of opposite sides are congruent.
3. By showing that one pair of opposite sides are both congruent and parallel.
4. By showing that both pairs of opposite angles are congruent.
5. By showing that the diagonals bisect each other.Lattices.ppt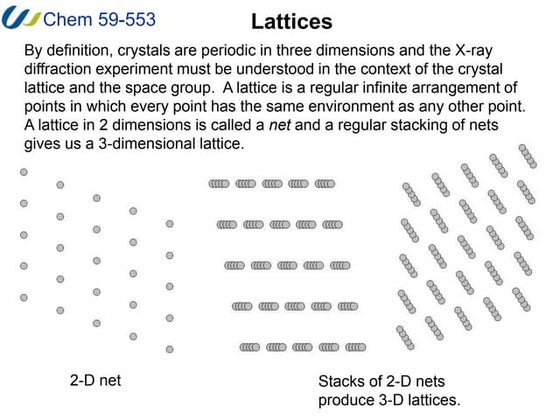



Lattices.pptRadhyesham
Ã˝
1. A lattice is a regular, infinite arrangement of points in which every point has the same environment as any other point. A 2D lattice is called a net and stacking of nets produces a 3D lattice.
2. The unit cell is the smallest repeating unit that generates the entire lattice through translations. It is defined by three distances (a, b, c) and three angles (α, β, γ).
3. There are 14 possible lattice arrangements, or Bravais lattices, that result from the 7 crystal systems which place different restrictions on the unit cell parameters. Lattices can have different types of centering.MT102 –õ–µ–∫—Ü 6



MT102 –õ–µ–∫—Ü 6ssuser184df1
Ã˝
1. The document discusses methods for calculating the area of regions bounded by curves using integral calculus.
2. Six methods are presented for computing the area of regions bounded above and below by curves including the use of polar coordinates.
3. One example calculates the area between the curves y=x2 and y=2x from x=0 to x=2 as 8π/15 using the integral of the difference of the two curves.9.5 Kites and Trapezoids



9.5 Kites and Trapezoidssmiller5
Ã˝
Use the properties of kites and trapezoids to solve problems
Classify quadrilaterals on a coordinate planeRecently uploaded (20)
How to Configure Deliver Content by Email in Odoo 18 Sales



How to Configure Deliver Content by Email in Odoo 18 SalesCeline George
Ã˝
In this slide, we’ll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Azure Data Engineer Interview Questions By ScholarHat



Azure Data Engineer Interview Questions By ScholarHatScholarhat
Ã˝
Azure Data Engineer Interview Questions By ScholarHatUnit 1 Computer Hardware for Educational Computing.pptx



Unit 1 Computer Hardware for Educational Computing.pptxRomaSmart1
Ã˝
Computers have revolutionized various sectors, including education, by enhancing learning experiences and making information more accessible. This presentation, "Computer Hardware for Educational Computing," introduces the fundamental aspects of computers, including their definition, characteristics, classification, and significance in the educational domain. Understanding these concepts helps educators and students leverage technology for more effective learning.Dr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptx



Dr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptxKhurshid Ahmed Ansari
Ã˝
Validity is an important characteristic of a test. A test having low validity is of little use. Validity is the accuracy with which a test measures whatever it is supposed to measure. Validity can be low, moderate or high. There are many factors which affect the validity of a test. If these factors are controlled, then the validity of the test can be maintained to a high level. In the power point presentation, factors affecting validity are discussed with the help of concrete examples.Functional Muscle Testing of Facial Muscles.pdf



Functional Muscle Testing of Facial Muscles.pdfSamarHosni3
Ã˝
Functional Muscle Testing of Facial Muscles.pdfEffective Product Variant Management in Odoo 18



Effective Product Variant Management in Odoo 18Celine George
Ã˝
In this slide we’ll discuss on the effective product variant management in Odoo 18. Odoo concentrates on managing product variations and offers a distinct area for doing so. Product variants provide unique characteristics like size and color to single products, which can be managed at the product template level for all attributes and variants or at the variant level for individual variants.BỘ TEST KIỂM TRA GIỮA KÌ 2 - TIẾNG ANH 10,11,12 - CHUẨN FORM 2025 - GLOBAL SU...



BỘ TEST KIỂM TRA GIỮA KÌ 2 - TIẾNG ANH 10,11,12 - CHUẨN FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
Ã˝
https://app.box.com/s/ij1ty3vm7el9i4qfrr41o756xycbahmgHow to Configure Recurring Revenue in Odoo 17 CRM



How to Configure Recurring Revenue in Odoo 17 CRMCeline George
Ã˝
This slide will represent how to configure Recurring revenue. Recurring revenue are the income generated at a particular interval. Typically, the interval can be monthly, yearly, or we can customize the intervals for a product or service based on its subscription or contract. How to create security group category in Odoo 17



How to create security group category in Odoo 17Celine George
Ã˝
This slide will represent the creation of security group category in odoo 17. Security groups are essential for managing user access and permissions across different modules. Creating a security group category helps to organize related user groups and streamline permission settings within a specific module or functionality.Year 10 The Senior Phase Session 3 Term 1.pptx



Year 10 The Senior Phase Session 3 Term 1.pptxmansk2
Ã˝
Year 10 The Senior Phase Session 3 Term 1.pptxNUTRITIONAL ASSESSMENT AND EDUCATION - 5TH SEM.pdf



NUTRITIONAL ASSESSMENT AND EDUCATION - 5TH SEM.pdfDolisha Warbi
Ã˝
NUTRITIONAL ASSESSMENT AND EDUCATION, Introduction, definition, types - macronutrient and micronutrient, food pyramid, meal planning, nutritional assessment of individual, family and community by using appropriate method, nutrition education, nutritional rehabilitation, nutritional deficiency disorder, law/policies regarding nutrition in India, food hygiene, food fortification, food handling and storage, food preservation, food preparation, food purchase, food consumption, food borne diseases, food poisoningAI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
Ã˝
AI and Academic Writing, Short Term Course in Academic Writing and Publication, UGC-MMTTC, MANUU, 25/02/2025, Prof. (Dr.) Vinod Kumar Kanvaria, University of Delhi, vinodpr111@gmail.comASP.NET Web API Interview Questions By Scholarhat



ASP.NET Web API Interview Questions By ScholarhatScholarhat
Ã˝
ASP.NET Web API Interview Questions By ScholarhatRRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
Ã˝
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.BỘ TEST KIỂM TRA GIỮA KÌ 2 - TIẾNG ANH 10,11,12 - CHUẨN FORM 2025 - GLOBAL SU...



BỘ TEST KIỂM TRA GIỮA KÌ 2 - TIẾNG ANH 10,11,12 - CHUẨN FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
Ã˝
AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
Ã˝
TRApezoids
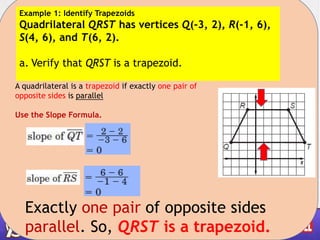
- 5. Example 1: Identify Trapezoids Quadrilateral QRST has vertices Q(-3, 2), R(-1, 6), S(4, 6), and T(6, 2). a. Verify that QRST is a trapezoid. A quadrilateral is a trapezoid if exactly one pair of opposite sides is parallel Use the Slope Formula. Exactly one pair of opposite sides parallel. So, QRST is a trapezoid.
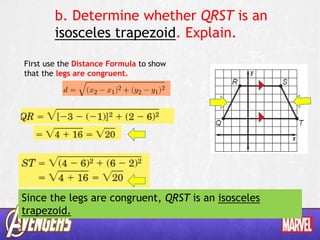
- 6. b. Determine whether QRST is an isosceles trapezoid. Explain. First use the Distance Formula to show that the legs are congruent. Since the legs are congruent, QRST is an isosceles trapezoid.
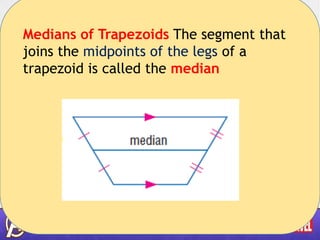
- 7. Medians of Trapezoids The segment that joins the midpoints of the legs of a trapezoid is called the median
- 8. Theorem 6.20
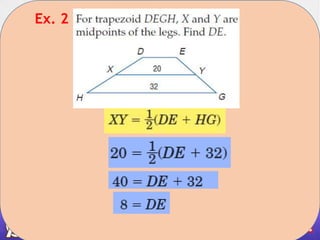
- 9. Ex. 2
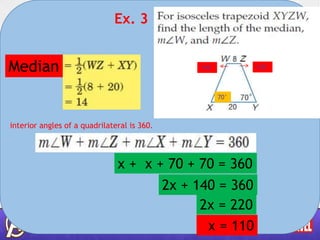
- 10. Ex. 3 Median 70° interior angles of a quadrilateral is 360. x + x + 70 + 70 = 360 2x + 140 = 360 2x = 220 x = 110 110°110°
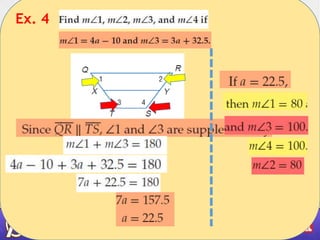
- 11. Ex. 4
- 12. Question 3 on page 358 Questions 4A and 4B on page 359 Questions 5-6, 18, 20, 21-22, and 25-26 on pages 359-369 Extra challenge Questions 1 and 7-10






