Triginometry
- 1. Answer these Questions: Type of the triangle in fig 1 WhatĪ»s the side opposite to right angle Called? Which property relate the sides of right triangle? fig1 P H B
- 2. ?
- 3. What Is Trigonometry? The word Ī░TrigonometryĪ▒ is derived from Greek words Ī«triĪ» (meaning three), Ī«gonĪ» (meaning sides) and Ī«metronĪ» (meaning measure). It is used to find Distances and Heights of objects in real life.
- 4. A trigonometric ratio is a ratio of the lengths of two sides in a right triangle. TRIGONOMETRIC RATIO
- 5. Three basic trigonometric ratios: sine cosine tangent each of which is the ratio of one side to another. .
- 6. How to Use Trigonometry Take the right-angled triangle ABC. Notice that A and C are acute angles and B is right angle. Acute angles are taken under consideration for finding T-ratios . A B C Hypotenuse Base Perpendicular
- 7. First, Label the Sides LetĪ»s take angle A under consideration. Each side is given a label in relation to angle Ī« A Ī». There is the hypotenuse , perpendicular and base side. A B C Hypotenuse Base Perpendicular
- 8. So, Now the Trigonometry As previously mentioned, the trigonometric functions: sine , cosine and tangent are ratios of the sides in relation to angle Ī« A Ī». A B C Hypotenuse Base Perpendicular
- 9. Firstly, Sine sine is shortened to Ī░sinĪ▒. Possible values of sine A are between 0 and 1. A B C Hypotenuse Base Perpendicular
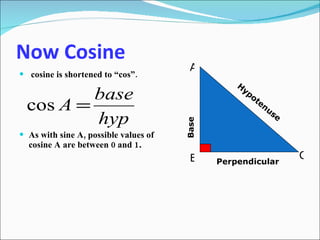
- 10. Now Cosine cosine is shortened to Ī░cosĪ▒. As with sine A, possible values of cosine A are between 0 and 1 . A B C Hypotenuse Base Perpendicular
- 11. And Finally Tangent tangent is shortened to Ī░tanĪ▒. Any value for tangent A is possible, both positive and negative. A B C Hypotenuse Base Perpendicular
- 12. opposite adjacent A B C Hypotenuse Base Perpendicular
- 13. S C T P B P H H B Sin P H Cos B H Tan P B
- 14. 6 8 10 A B C (P) (B) (H)
- 15. Identify perpendicular , hypotenuse and base in relation to angle C in given fig. A B C
- 16. Other Trigonometric-ratios Cosecant In short it is cosec. Secant In short it is sec. Cotangent In short it is cot.
- 17. ?
- 18. Example 1: Finding the Value of Trigonometric Ratio sin A, cos A, tan A,cosec A,sec A and cot A . A B C 17 15 8
- 19. sin A, cos A, tan A,cosec A,sec A and cot A . Sin A Cos A Tan A solution A B C 17 15 8
- 20. A B C 17 15 8
- 21. Find the values of all the trigonometric ratios of ? . 4 3 ? Pythagoras Theorem: (3) ? + (4)? = c? 5 = c 5
- 22. Example 2:If tan A=4/3 then calculate sinA.cosA SOLUTION A B C Let us first draw a right ABC As we know 3k 4k Therefore BC=4k,AB=3k, where k is any positive number. Now,by using Pythagoras theorem we have AC 2 = AB 2 + BC 2 =(3K) 2 +(4K) 2 =9K 2 + 16K 2 AC 2 =25K 2 AC=5K
- 23. A B C 4k 3k 5K Answer= 12/25
- 24. Students tend to make simple mistakes by mislabeling the perpendicular and base To overcome this mistake first determine the Hypotenuse. The side opposite to acute angle under Consideration is the perpendicular. COMMON ERROR ALERT
- 25. Find each trigonometric ratio. Sin B Cos B Tan B cosec B sec B cot B QUESTION 1 A C B 25 24 7
- 26. In ABC right angle at B, if calculate all other trigonometric ratios. QUESTION 2