2. Pengertian Sinus, Cosinus dan Tangen
留
r
y
x
r
y
=留sin
r
x
=留cos
x
y
=留tan
留
留
留
cos
sin
tan =
1cossin 22
=+ 留留
Berikut adalah beberapa
rumus-rumus
perbandingan geometri
yang akan sangat
berguna dalam
mempelajari materi ini :
3. A. Rumus Trigonometri Untuk Jumlah dan
Selisih Dua Sudut
Dengan mempelajari rumus trigonometri untuk
jumlah dan selisih dua sudut,kita dapat menentukan
fungsi trigonometri untuk sudut-sudut yang
merupakan jumlah atau selisih dua sudut istimewa.
Namun sebelum kita membahas mengenai rumus-
rumus tersebut, sebaiknya kita pahami terlebih
dahulu pengertian jumlah dua sudut dan selisih dua
sudut.
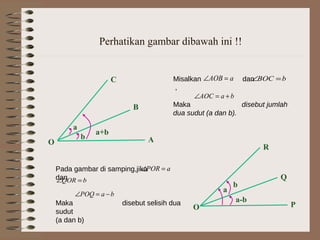
4. Perhatikan gambar dibawah ini !!
A
B
C
O
a
b
a+b
Misalkan dan
,
Maka disebut jumlah
dua sudut (a dan b).
aAOB = bBOC =
baAOC +=
a
a-b
b
P
Q
R
O
Pada gambar di samping,jika
dan
Maka disebut selisih dua
sudut
(a dan b)
aPOR =
bQOR =
baPOQ =
5. Rumus-rumus untuk cos(a+b) dan cos(a-b)
cos (a+b) = cos a cos b sin a sin b
tanda berlawanan
cos (a-b) = cos a cos b + sin a sin
b
tanda berlawanan
6. Contoh soal :
1) Jabarkanlah cos (4x+3y)!
Answer:
cos (4x+3y) = cos 4x cos 3y sin 4x sin 3y
2) Buktikan bahwa cos (90属- a) = sin a!
Answer :
cos (90属-a) = cos 90属 cos a + sin 90属 sin a
= 0 . cos a + 1 . sin a
= 0 + sin a
cos (90属-a) = sin a (proven)
7. Diketahui dan . Jika sudut A dan B
lancip,tentukan nilai cos (A-B)!
5
4
cos =A
5
3
cos =B
A B
4
5
? =
3
5
3
? =
4
5
4
sin
5
3
sin
=
=
B
A
BaBABA sinsincoscos)cos( +=
Answer:
5
4
.
5
3
5
3
.
5
4
+=
25
24
=
8. Buktikan bahwa : !!ba
ba
ba
tantan1
coscos
)cos(
=
+
ba
baba
ba
ba
coscos
sinsincoscos
coscos
)cos(
=
+
ba
ba
ba
ba
coscos
sinsin
coscos
coscos
=
ba
b
b
a
a
tantan1
cos
sin
.
cos
sin
1
=
=
(proven)
9. Rumus-rumus untuk sin (a+b) dan sin (a-b)
sin (a+b) = sin a cos b + cos a sin b
bertanda sama
sin (a-b) = sin a cos b - cos a sin b
bertanda sama
10. Contoh soal :
1) Jabarkanlah sin (4x-3y)!
Answer:
sin(4x-3y) = sin 4x cos 3y cos 4x sin 3y
2) Buktikan bahwa sin (180属-a) = sin a
Answer :
sin (180属-a) = sin 180属 cos a cos 180属 sin a
= 0 . cos a (-1) sin a
= 0 + sin a
sin (180属-a) = sin a (proven)
11. Diketahui dan . Sudut-sudut A dan B lancip.
Buktikan bahwa !
5
4
sin =A
13
5
sin =B
A B
? =
3
5
4
13
? =
12
5
13
12
cos
5
3
cos
=
=
B
A
babaBA sincoscossin)sin( =
Answer:
13
5
.
5
3
13
12
.
5
4
+=
65
33
)sin( = BA
65
33
)sin( = BA
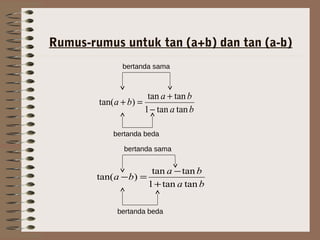
12. Rumus-rumus untuk tan (a+b) dan tan (a-b)
bertanda sama
bertanda sama
ba
ba
ba
tantan1
tantan
)tan(
+
=+
ba
ba
ba
tantan1
tantan
)tan(
+
=
bertanda beda
bertanda beda
13. Contoh soal :
1) Jabarkanlah tan (4x-3y)!
Answer:
2) Buktikan bahwa
Answer :
yx
yx
yx
3tan4tan1
3tan4tan
)34tan(
+
=
A
A
A
tan1
tan1
)45tan(
+
=+
A
A
A
tan45tan1
tan45tan
)45tan(
+
=+
A
A
tan.11
tan1
+
=
A
A
tan1
tan1
+
=
14. Diketahui dan . Sudut-sudut A dan B lancip.
Buktikan bahwa !
5
3
sin =A
13
12
cos =B
A B
? = 4
5
3
13
12
? =
5 4
3
tan
5
4
cos
=
=
A
A
BA
BA
BA
tantan1
tantan
)tan(
+
=Answer:
)(
63
16
63
48
.
48
16
48
15
48
48
48
20
48
36
12
5
.
4
3
1
12
5
4
3
proven==
+
=
+
=
63
16
)tan( = BA
12
5
tan
13
5
sin
=
=
B
B
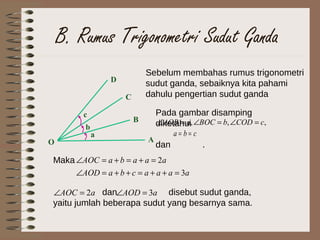
15. B. Rumus Trigonometri Sudut Ganda
A
B
C
O
a
b
D
c
Sebelum membahas rumus trigonometri
sudut ganda, sebaiknya kita pahami
dahulu pengertian sudut ganda
Pada gambar disamping
diketahui
dan .
,,, cCODbBOCaAOB ===
cba ==
Maka
dan disebut sudut ganda,
yaitu jumlah beberapa sudut yang besarnya sama.
aaaacbaAOD
aaabaAOC
3
2
=++=++=
=+=+=
aAOC 2= aAOD 3=
20. Dalam menentukan nilai perbandingan trigonometri
untuk sudut pertengahan, kita dapat menggunakan
rumus berikut :
2
2cos1
cos
a
a
+
賊=
2
2cos1
sin
a
a
賊=
a
a
a
2cos1
2cos1
tan
+
賊=
21. Contoh soal
Hitunglah nilai !!
2
1
22sin
2
2cos1
sin
a
a
賊=
Answer :
2
1
22sin tidak
negatif,maka :
2
45cos1
2
1
22sin
=
22
2
1
2
22
2
2
2
1
1
=
=
=
22. C. Rumus Perkalian
)cos()cos(coscos2 bababa ++=
)cos()cos(sinsin2 bababa +=
)cos()cos(sinsin2 bababa +=
Sejeni
s atau
)sin()sin(cossin2 bababa ++=
)sin()sin(sincos2 bababa +=
Tidak sejenis
23. Nyatakan bentuk-bentuk dibawah ini ke bentuk
jumlah atau selisih kosinus!
a)
Answer :
b)
Answer :
)sin()sin(2 yxyx +
)]()cos[()]()cos[()sin()sin(2 yxyxyxyxyxyx +++=+
xy 2cos2cos =
25sin65sin
]25sin.65sin2[
2
1
25sin65sin
=
40cos
2
1
)040(cos
2
1
)90cos40(cos
2
1
])2565cos()2565[cos(
2
1
==
=
+=
24. Nyatakan bentuk-bentuk dibawah ini ke bentuk
jumlah atau selisih sinus!
a)
Answer :
b)
Answer :
30cos50sin2
)3050sin()3050sin(30cos50sin2
++=
20sin80sin +=
)sin()cos(2 QPQP +
)]()sin[()]()sin[()sin()cos(2 QPQPQPQPQPQP +++=+
QP 2sin2sin =
![Nyatakan bentuk-bentuk dibawah ini ke bentuk
jumlah atau selisih kosinus!
a)
Answer :
b)
Answer :
)sin()sin(2 yxyx +
)]()cos[()]()cos[()sin()sin(2 yxyxyxyxyxyx +++=+
xy 2cos2cos =
25sin65sin
]25sin.65sin2[
2
1
25sin65sin
=
40cos
2
1
)040(cos
2
1
)90cos40(cos
2
1
])2565cos()2565[cos(
2
1
==
=
+=](https://image.slidesharecdn.com/trigonometri-130720083359-phpapp02/85/Trigonometri-23-320.jpg)
![Nyatakan bentuk-bentuk dibawah ini ke bentuk
jumlah atau selisih sinus!
a)
Answer :
b)
Answer :
30cos50sin2
)3050sin()3050sin(30cos50sin2
++=
20sin80sin +=
)sin()cos(2 QPQP +
)]()sin[()]()sin[()sin()cos(2 QPQPQPQPQPQP +++=+
QP 2sin2sin =](https://image.slidesharecdn.com/trigonometri-130720083359-phpapp02/85/Trigonometri-24-320.jpg)
![Nyatakan dalam bentuk perkalian!
a)
Answer :
b)
Answer :
AA 7cos9cos
)79(
2
1
sin)79(
2
1
sin27cos9cos AAAAAA +=
AAsin8sin2=
)2sin()2sin( 硫留硫留 +
硫留 sin2cos2=
)]2()2[(
2
1
sin)]2()2[(
2
1
cos2)2sin()2sin( 硫留硫留硫留硫留硫留硫留 +++=+](https://image.slidesharecdn.com/trigonometri-130720083359-phpapp02/85/Trigonometri-27-320.jpg)
![Jika , maka buktikan bahwa :
180=++ CBA
CBACBA sinsinsin4sin2sin2sin2 =++
CBA sin2sin2sin2 ++
Answer :
))(180cos(sin2)cos()180sin(2 BACBAC ++=
CCBABA cossin2)cos()sin(2 ++=
))cos((sin2)cos(sin2 BACBAC ++=
CBA
BAC
BABAC
sinsinsin4
)]sin(sin2[sin2
)]cos()[cos(sin2
=
=
+=
(proven)](https://image.slidesharecdn.com/trigonometri-130720083359-phpapp02/85/Trigonometri-29-320.jpg)
