Triunghiul dreptunghic
- 1. Prof. Rad Aurelian Florin TRIUNGHIUL DREPTUNGHIC
- 2. TRIUNGHIUL DREPTUNGHIC DESCRIERE B C A m(<A) = 900 m(<B) < 900 m(<C) < 900 m(<B) + m(<C) = 900 AB , AC = catete BC = ipotenuz
- 3. TRIUNGHIUL DREPTUNGHIC PERIMETRUL I ARIA A B C D P ABC = AB + AC + BC AABC 2 ACAB = ABC A 2 ADBC =
- 4. TRIUNGHIUL DREPTUNGHIC TEOREMA LUI PITAGORA A B C ntr-un triunghi dreptunghic, suma ptratelor catetelor este egal cu ptratul ipotenuzei. catet 2 + catet 2 = ipotenuz 2 AB 2 + AC 2 = BC2
- 5. TRIUNGHIUL DREPTUNGHIC RECIPROCA TEOREMEI LUI PITAGORA A B C Dac 樽ntr-un triunghi, suma ptratelor a dou laturi este egal cu ptratul celei de-a treia laturi, atunci triunghiul este dreptunghic. AB2 + AC2 = BC2 m(<A)=90
- 6. TRIUNGHIUL DREPTUNGHIC TEOREMA NL鄭IMII A C B D AD BC ; AD = inl釘imea BD,CD=proiec釘iile catetelor pe ipotenuz nl釘imea corespunztoare ipotenuzei este media geometric a proiec釘iilor catetelor pe ipotenuz. AD2 = BD CD Relatia dintre inaltime si laturile triunghiului: AD = BC ACAB
- 7. TRIUNGHIUL DREPTUNGHIC TEOREMA CATETEI A B D C AD BC ; AD = inl釘imea BD,CD=proiec釘iile catetelor pe ipotenuz Cateta este media geometric dintre ipotenuz i proiec釘ia catetei pe ipotenuz. AB2 = BC BD AC2 = BC CD
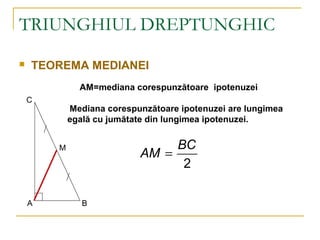
- 8. TRIUNGHIUL DREPTUNGHIC TEOREMA MEDIANEI A B C M AM=mediana corespunztoare ipotenuzei Mediana corespunztoare ipotenuzei are lungimea egal cu jumtate din lungimea ipotenuzei. 2 BC AM =
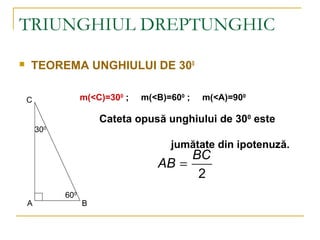
- 9. TRIUNGHIUL DREPTUNGHIC TEOREMA UNGHIULUI DE 300 A B C 300 600 m(<C)=300 ; m(<B)=600 ; m(<A)=900 Cateta opus unghiului de 300 este jumtate din ipotenuz. 2 BC AB =
- 10. TRIUNGHIUL DREPTUNGHIC RAPOARTE CONSTANTE: sin , cos, tg , ctg ipotenuz opcateta SINUS . = relatii intre unghiuri si laturi ipotenuz alcateta COSINUS . = . . alcateta opcateta TANGENTA = . . opcateta alcateta COTANGENTA =
- 11. TRIUNGHIUL DREPTUNGHIC VALORILE UZUALE ALE FUNC鄭IILOR TRIGONOMETRICE 300 600 450 SIN COS TG CTG 2 3 2 3 2 1 2 1 3 1 3 1 3 3 1 1 2 2 2 2