ݺߣ

ݺߣShare a Scribd company logo

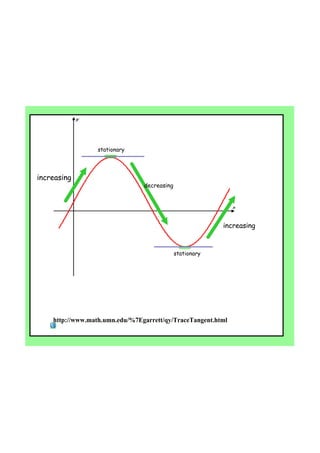
IB Maths. Turning points. First derivative test

?
?
E
estelav

By the end of the lesson, students will be able to use derivatives to find maximum and minimum points of a function, and use second derivatives to determine the nature of stationary points and points of inflection. Specifically, they will learn that: (1) if the first derivative is zero at a point, it is a stationary point; (2) the second derivative test can determine if it is a local max, min or point of inflection; and (3) points of inflection occur when the curve changes concavity. Students will apply these concepts to find the stationary points of sample functions and classify their nature.

Convert to study materialsBETA

Transform any presentation into ready-made study materialselect from outputs like summaries, definitions, and practice questions.

1 of 14
Downloaded 40 times
By?the?end?of?the?lesson?you?will?be?able?to: ? Use?the?derivative?of?a?function?to?find? ????maximum?and?minimum?points. ? Use?the?second?derivative?to?test?the?nature?of?a? stationary?point?and/or?point?of?inflexion.
increasing increasing decreasing stationary stationary http://www.math.umn.edu/%7Egarrett/qy/TraceTangent.html
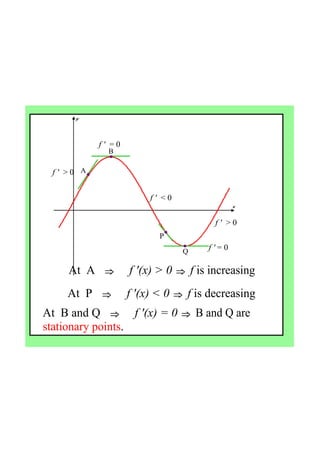
? ? ? ? ? ? ? ? A B P Q At??A???? ?f?'(x)?>?0?? f?is?increasing ????????? At??P???? ?f?'(x)?<?0?? f?is?decreasing ????????? At??B?and?Q???? ?f?'(x)?=?0?? B?and?Q?are? stationary?points.????????? f?'??=?0 f?'??<?0 f?'??>?0 f?'??>?0 f?'?=?0
If the derivative is positive then the function is increasing. If the derivative is negative then the function is decreasing. ?
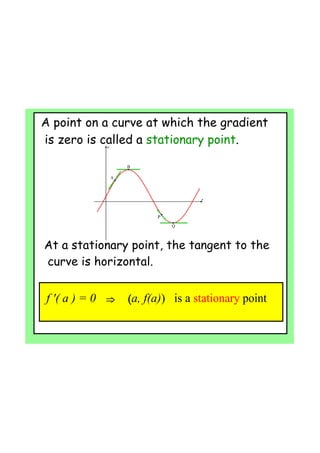
f?'(?a?)?=?0???? (a,?f(a))???is?a?stationary?point ? ? ? ? ? ? ? ? A B P Q A point on a curve at which the gradient is zero is called a stationary point. At a stationary point, the tangent to the curve is horizontal.
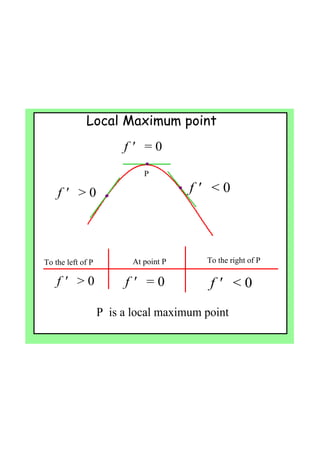
? ? ? ? ? ? Local Maximum point ?f?'???>?0 ?f?'???=?0 ?f?'???<?0 P To?the?left?of?P At?point?P To?the?right?of?P ?f?'???>?0 ?f?'???<?0?f?'???=?0 P??is?a?local?maximum?point
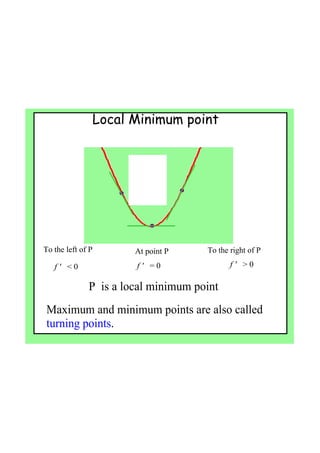
Local Minimum point ?f?'???>?0 ?f?'???=?0 ?f?'???<?0 To?the?left?of?P At?point?P To?the?right?of?P ?f?'???>?0?f?'???<?0 ?f?'???=?0 P??is?a?local?minimum?point P ? ? ? ?? ? Maximum?and?minimum?points?are?also?called? turning?points.
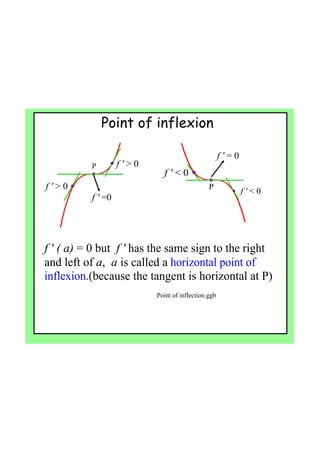
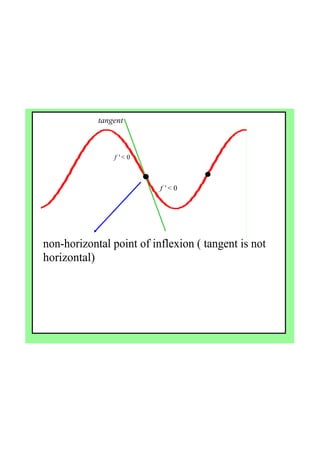
Point of inflexion ? ? ? ? ? ? f?'?=0 f?'?>?0 f?'?>?0P ? ? ? ? ? ? f?'?=?0 f?'?<?0 f?'?<?0 P f?'?(?a)?=?0?but??f?'?has?the?same?sign?to?the?right? and?left?of?a,??a?is?called?a?horizontal?point?of? inflexion.(because?the?tangent?is?horizontal?at?P) Point?of?inflection.ggb
? ? non?horizontal?point?of?inflexion?(?tangent?is?not? horizontal) f?'?<?0 f?'?<?0 tangent ? ?
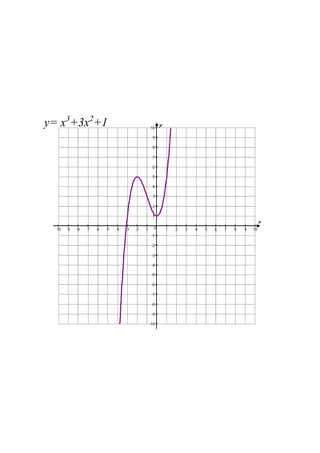
Find?the?coordinates?of?the?stationary?points?on?the? curve?y=?x3 +3x2 +1?and?determine?their?nature.
y=?x3 +3x2 +1?
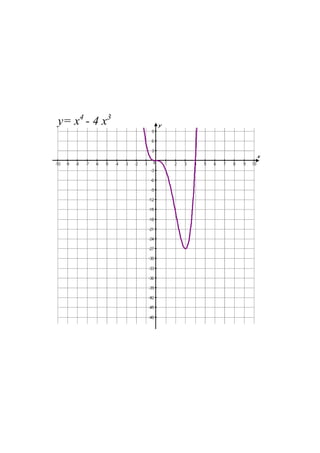
Find?the?coordinates?of?the?stationary?points?on?the? curve?y=?x4? ??4?x3 ??and?determine?their?nature.
y=?x4? ??4?x3 ?
Attachments Point?of?inflection.ggb

More Related Content

IB Maths. Turning points. First derivative test