Tutorial on EM algorithm - Poster
Maximum likelihood estimation (MLE) is a popular method for parameter estimation in both applied probability and statistics but MLE cannot solve the problem of incomplete data or hidden data because it is impossible to maximize likelihood function from hidden data. Expectation maximum (EM) algorithm is a powerful mathematical tool for solving this problem if there is a relationship between hidden data and observed data. Such hinting relationship is specified by a mapping from hidden data to observed data or by a joint probability between hidden data and observed data (showing MLE, EM, and practical EM, hidden info implies the hinting relationship). The essential ideology of EM is to maximize the expectation of likelihood function over observed data based on the hinting relationship instead of maximizing directly the likelihood function of hidden data (showing the full EM with proof along with two steps). An important application of EM is (finite) mixture model which in turn is developed towards two trends such as infinite mixture model and semiparametric mixture model. Especially, in semiparametric mixture model, component probabilistic density functions are not parameterized. Semiparametric mixture model is interesting and potential for other applications where probabilistic components are not easy to be specified (showing mixture models). I raise a question that whether it is possible to backward discover semiparametric EM from semiparametric mixture model. I hope that this question will open a new trend or new extension for EM algorithm (showing the question).
Tutorial on EM algorithm - Poster
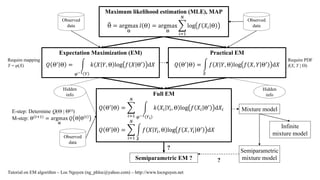
- 1. Presentation Maximum likelihood estimation (MLE) is a popular method for parameter estimation in both applied probability and statistics but MLE cannot solve the problem of incomplete data or hidden data because it is impossible to maximize likelihood function from hidden data. Expectation maximum (EM) algorithm is a powerful mathematical tool for solving this problem if there is a relationship between hidden data and observed data. Such hinting relationship is specified by a mapping from hidden data to observed data or by a joint probability between hidden data and observed data (showing MLE, EM, and practical EM, hidden info implies the hinting relationship). The essential ideology of EM is to maximize the expectation of likelihood function over observed data based on the hinting relationship instead of maximizing directly the likelihood function of hidden data (showing the full EM with proof along with two steps). An important application of EM is (finite) mixture model which in turn is developed towards two trends such as infinite mixture model and semiparametric mixture model. Especially, in semiparametric mixture model, component probabilistic density functions are not parameterized. Semiparametric mixture model is interesting and potential for other applications where probabilistic components are not easy to be specified (showing mixture models). I raise a question that whether it is possible to backward discover semiparametric EM from semiparametric mixture model. I hope that this question will open a new trend or new extension for EM algorithm (showing the question).
- 2. Maximum likelihood estimation (MLE), MAP = argmax = argmax =1 log Expectation Maximization (EM) = 1 , log d Practical EM = , log , d Full EM = =1 1 , log d = =1 , log , d Observed data Observed data Observed data Mixture model Semiparametric EM ? ? E-step: Determine Q( | (t)) M-step: +1 = argmax Require mapping Y = (X) Require PDF f(X, Y | 牢) ? Tutorial on EM algorithm Loc Nguyen (ng_phloc@yahoo.com) http://www.locnguyen.net Semiparametric mixture model Infinite mixture model Hidden info Hidden info
- 3. Thank you for attention 3 Conditional mixture model for modeling attributed dyadic data 16/09/2021
Editor's Notes
- #3: Maximum likelihood estimation (MLE) is a popular method for parameter estimation in both applied probability and statistics but MLE cannot solve the problem of incomplete data or hidden data because it is impossible to maximize likelihood function from hidden data. Expectation maximization (EM) algorithm is a powerful mathematical tool for solving this problem if there is a relationship between hidden data and observed data. Such hinting relationship is specified by a mapping from hidden data to observed data or by a joint probability between hidden data and observed data (showing MLE, EM, and practical EM, hidden info implies the hinting relationship). The essential ideology of EM is to maximize the expectation of likelihood function over observed data based on the hinting relationship instead of maximizing directly the likelihood function of hidden data (showing the full EM with proof along with two steps). An important application of EM is (finite) mixture model which in turn is developed towards two trends such as infinite mixture model and semiparametric mixture model. Especially, in semiparametric mixture model, component probabilistic density functions are not parameterized. Semiparametric mixture model is interesting and potential for other applications where probabilistic components are not easy to be specified (showing mixture models). I raise a question that whether it is possible to backward discover semiparametric EM from semiparametric mixture model. I hope that this question will open a new trend or new extension for EM algorithm (showing the question).