Uji asumsi klasik
•Download as DOCX, PDF•
6 likes•49,128 views
Terdapat 5 uji asumsi klasik yang perlu dilakukan untuk model regresi, yaitu: (1) multikolinearitas, (2) autokorelasi, (3) heteroskedastisitas, (4) normalitas, dan (5) linearitas. Hasil uji pada contoh penelitian menunjukkan bahwa model regresi memenuhi semua asumsi klasik tersebut.
Uji asumsi klasik
- 1. Uji Asumsi Klasik | 1 Uji Asumsi Klasik Tujuan pengujian asumsi klasik ini adalah untuk memberikan kepastian bahwa persamaan regresi yang didapatkan memiliki ketepatan dalam estimasi, tidak bias dan konsisten. Perlu diketahui, terdapat kemungkinan data aktual tidak memenuhi semua asumsi klasik ini. Beberapa perbaikan, baik pengecekan kembali data outlier maupun recollecterror data dapat dilakukan. Uji asumsi klasik yang dikemukakan dalam modul ini antara lain: uji multikolinearitas, uji autokorelasi, uji heteroskedastisitas, uji normalitas dan uji linearitas. 1. Uji Asumsi Multikolinieritas Tujuan digunakannya uji ini adalah untuk menguji apakah pada model regresi ditemukan adanya korelasi antar variabel independen. Jika terdapat atau terjadi korelasi, maka dinamakan terdapat problem multikolinieritas (multiko). Model regresi yang baik seharusnya tidak terjadi kerelasi di antara variabel independen. Kasus: Seorang peneliti ingin menguji asumsimultikolinieritas dari variabel Kinerja Karyawan (Y), Struktur Organisasi (X1), Budaya Organisasi (X2) dan Kepemimpinan (X3). Langkah-Langkah: 1) Masukkan data X1, X2, X3 dan Y yang terdapat pada lampiran. 2) Pilih menu Analize kemudian submenu Regression, lalu pilih Linear.
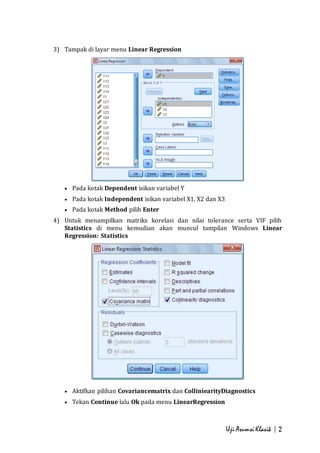
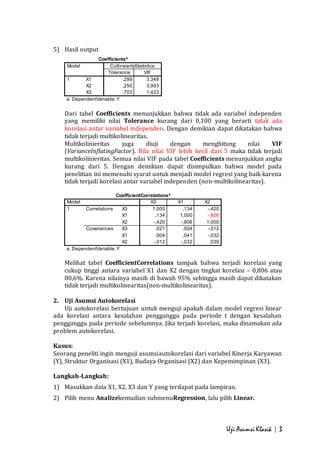
- 2. Uji Asumsi Klasik | 2 3) Tampak di layar menu Linear Regression ï‚· Pada kotak Dependent isikan variabel Y ï‚· Pada kotak Independent isikan variabel X1, X2 dan X3 ï‚· Pada kotak Method pilih Enter 4) Untuk menampilkan matriks korelasi dan nilai tolerance serta VIF pilih Statistics di menu kemudian akan muncul tampilan Windows Linear Regression: Statistics ï‚· Aktifkan pilihan Covariancematrix dan ColliniearityDiagnostics ï‚· Tekan Continue lalu Ok pada menu LinearRegression
- 3. Uji Asumsi Klasik | 3 5) Hasil output Coefficientsa Model CollinearityStatistics Tolerance VIF 1 X1 ,299 3,348 X2 ,250 3,993 X3 ,703 1,423 a. DependentVariable: Y Dari tabel Coefficients menunjukkan bahwa tidak ada variabel independen yang memiliki nilai Tolerance kurang dari 0,100 yang berarti tidak ada korelasi antar variabel independen. Dengan demikian dapat dikatakan bahwa tidak terjadi multikolinearitas. Multikolinieritas juga diuji dengan menghitung nilai VIF (VarianceInflatingFactor). Bila nilai VIF lebih kecil dari 5 maka tidak terjadi multikolinieritas. Semua nilai VIF pada tabel Coefficients menunjukkan angka kurang dari 5. Dengan demikian dapat disimpulkan bahwa model pada penelitian ini memenuhi syarat untuk menjadi model regresi yang baik karena tidak terjadi korelasi antar variabel independen (non-multikolinearitas). CoefficientCorrelationsa Model X3 X1 X2 1 Correlations X3 1,000 ,134 -,420 X1 ,134 1,000 -,806 X2 -,420 -,806 1,000 Covariances X3 ,021 ,004 -,012 X1 ,004 ,041 -,032 X2 -,012 -,032 ,039 a. DependentVariable: Y Melihat tabel CoefficientCorrelations tampak bahwa terjadi korelasi yang cukup tinggi antara variabel X1 dan X2 dengan tingkat korelasi – 0,806 atau 80,6%. Karena nilainya masih di bawah 95% sehingga masih dapat dikatakan tidak terjadi multikolinearitas(non-multikolinearitas). 2. Uji Asumsi Autokorelasi Uji autokorelasi bertujuan untuk menguji apakah dalam model regresi linear ada korelasi antara kesalahan pengganggu pada periode t dengan kesalahan pengganggu pada periode sebelumnya. Jika terjadi korelasi, maka dinamakan ada problem autokorelasi. Kasus: Seorang peneliti ingin menguji asumsiautokorelasi dari variabel Kinerja Karyawan (Y), Struktur Organisasi (X1), Budaya Organisasi (X2) dan Kepemimpinan (X3). Langkah-Langkah: 1) Masukkan data X1, X2, X3 dan Y yang terdapat pada lampiran. 2) Pilih menu Analizekemudian submenuRegression, lalu pilih Linear.
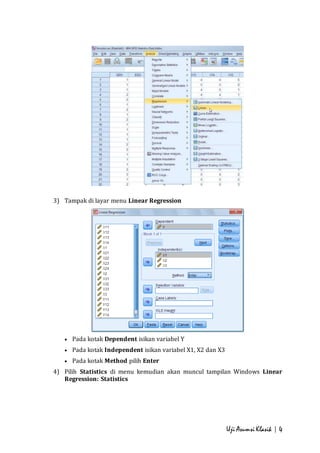
- 4. Uji Asumsi Klasik | 4 3) Tampak di layar menu Linear Regression ï‚· Pada kotak Dependent isikan variabel Y ï‚· Pada kotak Independent isikan variabel X1, X2 dan X3 ï‚· Pada kotak Method pilih Enter 4) Pilih Statistics di menu kemudian akan muncul tampilan Windows Linear Regression: Statistics
- 5. 1 ,710a ,504 ,474 1,319 1,844 a. Predictors: (Constant), X3, X1, X2 b. DependentVariable: Y Uji Asumsi Klasik | 5 ï‚· Aktifkan pilihan Durbin-Watson ï‚· Tekan Continue lalu Ok pada menu Linear Regression 5) Hasil output Model Summaryb Model R R Square Adjusted R Square Std. Error of theEstimate Durbin-Watson di me ns i o n0 Nilai DW sebesar 1,844 akan dibandingkan dengan nilai tabel yang memiliki signifikansi 5%, jumlah sampel 54 dan jumlah variabel independen 3. Oleh karena nilai ini lebih besar dari batas atas (du) 1,681 dan kurang dari 4-du, maka dapat disimpulkan tidak terdapat autokorelasi. 3. Uji Asumsi Heteroskedastisitas. Uji ini bertujuan untuk menguji apakah dalam model regresi terjadi atau terdapat ketidaksamaan varians dari rersidual dari satu pengamatan ke pengamatan yang lain. Jika varians dari nilai residual dari satu pengamatan ke pengamatan yang lain tetap, maka disebut dengan Homokedastisitas. Dan jika varians berbeda dari satu pengamatan ke pengamatan yang lainnya, maka disebut Heteroskedastisitas. Menurut Singgih Santoso dalam bukunya yang berjudul Buku Latihan SPSS Statistik Parametrik, menyabutkan bahwa model regresi yang baik adalah yang tidak terjadi Heteroskedastisitas, atau dengan kata lain model regresi yang baik adalah yang Homokedastisitas. Kasus:
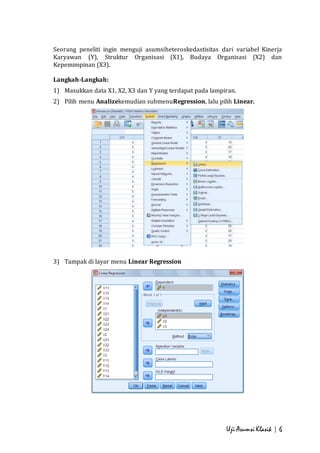
- 6. Seorang peneliti ingin menguji asumsiheteroskedastisitas dari variabel Kinerja Karyawan (Y), Struktur Organisasi (X1), Budaya Organisasi (X2) dan Kepemimpinan (X3). Langkah-Langkah: 1) Masukkan data X1, X2, X3 dan Y yang terdapat pada lampiran. 2) Pilih menu Analizekemudian submenuRegression, lalu pilih Linear. Uji Asumsi Klasik | 6 3) Tampak di layar menu Linear Regression
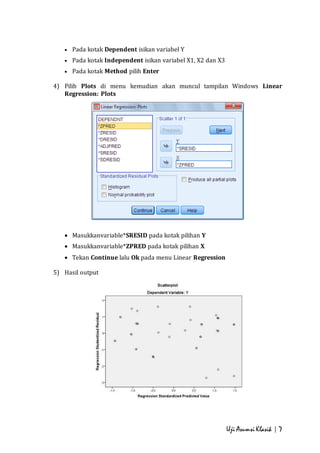
- 7. Uji Asumsi Klasik | 7 ï‚· Pada kotak Dependent isikan variabel Y ï‚· Pada kotak Independent isikan variabel X1, X2 dan X3 ï‚· Pada kotak Method pilih Enter 4) Pilih Plots di menu kemudian akan muncul tampilan Windows Linear Regression: Plots ï‚· Masukkanvariable*SRESID pada kotak pilihan Y ï‚· Masukkanvariable*ZPRED pada kotak pilihan X ï‚· Tekan Continue lalu Ok pada menu Linear Regression 5) Hasil output
- 8. Dari grafik Scatterplot terlihat bahwa titik-titik menyebar secara acak serta tersebar baik diatas maupun dibawah angka nol pada sumbu Y. Jadi dapat disimpulkan bahwa model pada penelitian ini memenuhi syarat untuk menjadi model yang baik karena merupakan model yang homoskedastisitas atau varians dari nilai residual pengamatan satu ke pengamatan yang lain tetap. Uji Asumsi Klasik | 8 4. Uji asumsi Normalitas Uji ini bertujuan untuk menguji apakah dalam sebuah model regresi, variabel independen, variabel dependen, atau keduanya mempunyai distribusi normal atau tidak. Suatu model regresi yang baik adalah yang memiliki distribusi data normal atau mendekati normal. Kasus: Seorang peneliti ingin menguji asumsiheteroskedastisitas dari variabel Kinerja Karyawan (Y), Struktur Organisasi (X1), Budaya Organisasi (X2) dan Kepemimpinan (X3). Langkah-Langkah: 1) Masukkan data X1, X2, X3 dan Y yang terdapat pada lampiran. 2) Pilih menu Analizekemudian submenuRegression, lalu pilih Linear.
- 9. Uji Asumsi Klasik | 9 3) Tampak di layar menu Linear Regression ï‚· Pada kotak Dependent isikan variabel Y ï‚· Pada kotak Independent isikan variabel X1, X2 dan X3 ï‚· Pada kotak Method pilih Enter 4) Pilih Plots di menu kemudian akan muncul tampilan Windows Linear Regression: Plots ï‚· Aktifkan pilihan Histogram dan Normal probability plot ï‚· Tekan Continue lalu Ok pada menu Linear Regression
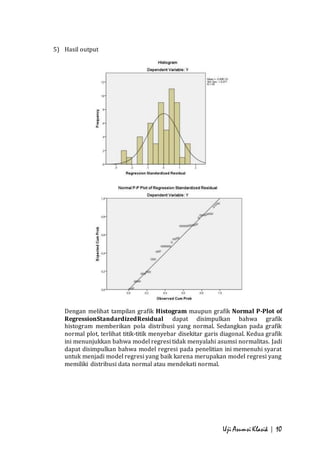
- 10. Uji Asumsi Klasik | 10 5) Hasil output Dengan melihat tampilan grafik Histogram maupun grafik Normal P-Plot of RegressionStandardizedResidual dapat disimpulkan bahwa grafik histogram memberikan pola distribusi yang normal. Sedangkan pada grafik normal plot, terlihat titik-titik menyebar disekitar garis diagonal. Kedua grafik ini menunjukkan bahwa model regresi tidak menyalahi asumsi normalitas. Jadi dapat disimpulkan bahwa model regresi pada penelitian ini memenuhi syarat untuk menjadi model regresi yang baik karena merupakan model regresi yang memiliki distribusi data normal atau mendekati normal.
- 11. Uji Asumsi Klasik | 11 5. Uji Asumsi Linearitas Uji linieritas dilakukan dengan melihat scatterplot antara standar residual dengan prediksinya. Bila sebaran tidak menunjukkan pola tertentu maka dikatakan asumsi linieritas memenuhi syarat. Hasil pengujian menunjukkan scatterplot tidak membentuk pola tertentu sehingga dapat disimpulkan bahwa model pada penelitian ini memenuhi syarat untuk menjadi model yang baik karena asumsi linieritasterpenuhi.