Ukuran Pemusatan Data - Materi ke-9.pptx
- 1. Probabilitas dan Statistika UKURAN PEMUSATAN DATA Rekayasa Sistem Komputer Universitas Tanjungpura Pontianak 2023
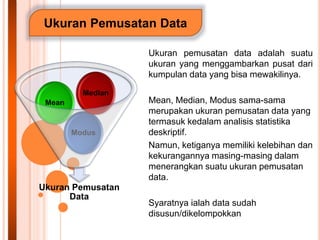
- 2. Ukuran Pemusatan Data Ukuran pemusatan data adalah suatu ukuran yang menggambarkan pusat dari kumpulan data yang bisa mewakilinya. Mean, Median, Modus sama-sama merupakan ukuran pemusatan data yang termasuk kedalam analisis statistika deskriptif. Namun, ketiganya memiliki kelebihan dan kekurangannya masing-masing dalam menerangkan suatu ukuran pemusatan data. Syaratnya ialah data sudah disusun/dikelompokkan Ukuran Pemusatan Data Modus Mean Median
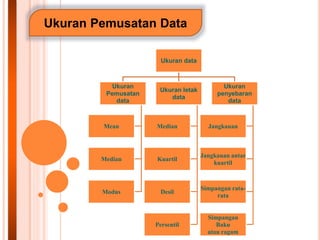
- 3. Ukuran Pemusatan Data Ukuran data Ukuran Pemusatan data Mean Median Modus Ukuran letak data Median Kuartil Desil Persentil Ukuran penyebaran data Jangkauan Jangkauan antar kuartil Simpangan rata- rata Simpangan Baku atau ragam
- 4. Data Tunggal Data tunggal : data yang belum tersusun atau dikelompokkan ke dalam kelas-kelas interval. Perhitungan Frekuensi data tak berkelompok, biasanya setiap data mewakili data tersebut secara tunggal. x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 3 3 4 5 5 5 7 8 9 9
- 5. Data Berkelompok Data berkelompok adalah data yang telah digolongkan dalam distribusi frekuensi. Data berkelompok biasanya disajikan dalam bentuk tabel yang terdiri dari beberapa kelas. Yang dimaksud dengan kelas di sini adalah suatu bagian/elemen dari tabel yang menunjukkan jumlah data yang berada pada suatu rentang tertentu. Nomor Fi 10 14 3 15 19 6 20 24 9
- 6. Data Berkelompok Mengubah Data Tunggal Menjadi Data Berkelompok 1. Cari Jangkauan dengan rumus J = Xmaks Xmin 2. Setelah mencari jangkauan kita mencari banyak kelas dengan kaidah empiris Sturgess k = 1+3.3 log n (n =banyak Data) 3. Cari panjang kelas dengan rumus C = J:k (pembulatan ke atas) 4. Tentukan frekuensi tiap kelasnya
- 7. Pembahasan TK-01 2. Ubah data tunggal berikut ini ke dalam bentuk data Kelompok.
- 8. Pembahasan TK-01 2. Ubah data tunggal berikut ini ke dalam bentuk data Kelompok. Interval Nilai fi BB BA 119 127 3 128 136 4 137 145 10 146 154 14 155 163 4 164 172 3 173 181 2
- 10. Mean Perhitungan rata-rata (mean) didapat dari jumlah nilai seluruh data dibagi dengan banyaknya data. Ini bisa dilakukan baik untuk data tunggal maupun data berkelompok. Mean Data Tunggal Perhitungan rata-rata () untuk data tunggal menggunakan rumus sebagai berikut : = ヰ ヰ = Penjumlahan unsur pada variabel n = jumlah subjek
- 11. Mean Contoh Soal Mean Data Tunggal Usia tujuh orang mahasiswa Program Studi Teknik Informatika adalah : 19, 20,18, 26 ,21, 23, 24. Berapakah rata-rata usia ke tujuh orang mahasiswa tersebut ? = ヰ
- 12. Mean Mean Data Berkelompok Perhitungan rata-rata () untuk data berkelompok menggunakan rumus sebagai berikut : = ヰ ヰ = nilai-nilai pengamatan yang diwakili dengan nilai tengah kelas = frekuensi relatif tiap kelas interval = n = jumlah subjek
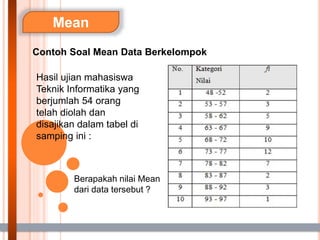
- 13. Mean Contoh Soal Mean Data Berkelompok Hasil ujian mahasiswa Teknik Informatika yang berjumlah 54 orang telah diolah dan disajikan dalam tabel di samping ini : Berapakah nilai Mean dari data tersebut ?
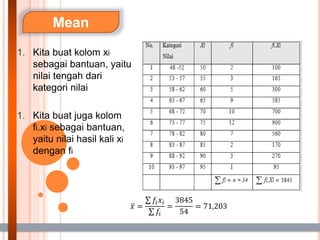
- 14. Mean 1. Kita buat kolom xi sebagai bantuan, yaitu nilai tengah dari kategori nilai 1. Kita buat juga kolom fi.xi sebagai bantuan, yaitu nilai hasil kali xi dengan fi = ヰ = 3845 54 = 71,203
- 15. Median Median adalah nilai yang persis berada di tengah jika suatu angkatan data diurutkan dari nilai terkecil / terendah sampai terbesar / tertinggi atau sebaliknya. Perhitungan median juga menggunakan teknik yang berbeda antara data tak berkelompok/tunggal dengan data berkelompok atau bergolong. Median Data Tunggal Ada satu kelompok nilai yang telah diurutkan sebagai berikut : 60, 61, 62, 64, 65, 66, 67. Untuk kelompok nilai tadi, mediannya adalah 64 karena persis berada di tengah. Nilai : 60, 61, 62, 64, 65, 66, 67, 68 Nilai yang persis di tengah dari urutan nilai di atas bukan lagi satu nilai tetapi telah menjadi dua nilai yaitu 64, dan 65. Me =
- 16. Median Data Berkelompok Untuk data berkelompok menentukan mediannya () diawali dengan menentukan kelas median, kemudian menentukan median kelas tersebut dengan persamaan berikut : = + 2 n = jumlah individu frekuensi = frekuensi relatif kelas median = frekuensi kumulatif sebelum kelas yang dimaksud = tepi bawah = ( BB 0,5 ) = interval/panjang kelas = (BA BB) + 1
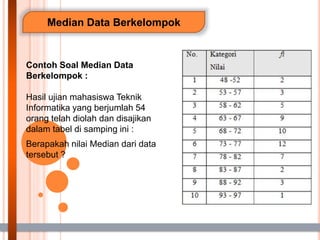
- 17. Median Data Berkelompok Contoh Soal Median Data Berkelompok : Hasil ujian mahasiswa Teknik Informatika yang berjumlah 54 orang telah diolah dan disajikan dalam tabel di samping ini : Berapakah nilai Median dari data tersebut ?
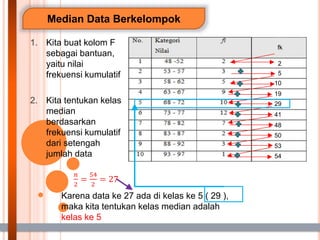
- 18. Median Data Berkelompok 1. Kita buat kolom F sebagai bantuan, yaitu nilai frekuensi kumulatif 2. Kita tentukan kelas median berdasarkan frekuensi kumulatif dari setengah jumlah data fk 5 10 19 29 41 48 50 53 54 2 Karena data ke 27 ada di kelas ke 5 ( 29 ), maka kita tentukan kelas median adalah kelas ke 5
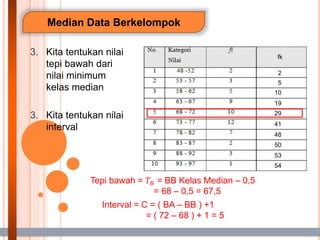
- 19. Median Data Berkelompok 3. Kita tentukan nilai tepi bawah dari nilai minimum kelas median 3. Kita tentukan nilai interval fk 5 10 19 29 41 48 50 53 54 2 Tepi bawah = = BB Kelas Median 0,5 = 68 0,5 = 67,5 Interval = C = ( BA BB ) +1 = ( 72 68 ) + 1 = 5
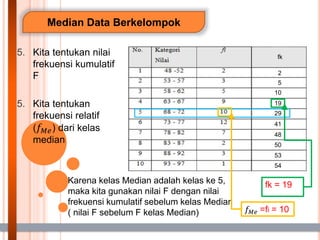
- 20. Median Data Berkelompok 5. Kita tentukan nilai frekuensi kumulatif F 5. Kita tentukan frekuensi relatif () dari kelas median fk 5 10 19 29 41 48 50 53 54 2 Karena kelas Median adalah kelas ke 5, maka kita gunakan nilai F dengan nilai frekuensi kumulatif sebelum kelas Median ( nilai F sebelum F kelas Median) fk = 19 =fi = 10
- 21. Median Data Berkelompok 8. Kita hitung median ( Me ) dengan menggunakan rumus Median untuk data berkelompok = + 2 = 67,5 + 54 2 19 10 5
- 22. 22 Modus Modus dapat dipahami sebagai nilai yang sering muncul atau suatu kelompok nilai yang memiliki frekuensi relatif terbesar. Modus Data Tunggal Perhitungan modus untuk data tunggal menggunakan rumus sebagai berikut : x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 3 3 4 5 5 5 7 8 9 9 Modus ( Mo ) = 5
- 23. Modus Data Berkelompok Modus Data Berkelompok Perhitungan modus () untuk data berkelompok menggunakan rumus sebagai berikut : = + 1 1 + 2 1 = frekuensi relatif kelas modus dikurangi frekueinsi relatif kelas sebelumnya 2 = frekuensi relatif kelas modus dikurangi frekueinsi relatif kelas berikutnya = tepi bawah = ( BB 0,5 ) = interval/panjang kelas = (BA BB) + 1
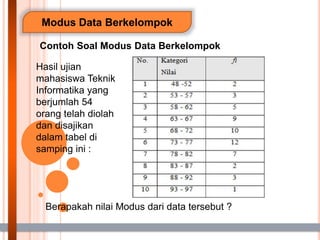
- 24. Modus Data Berkelompok Contoh Soal Modus Data Berkelompok Hasil ujian mahasiswa Teknik Informatika yang berjumlah 54 orang telah diolah dan disajikan dalam tabel di samping ini : Berapakah nilai Modus dari data tersebut ?
- 25. Modus Data Berkelompok 1. Kita tentukan kelas Modus dengan memilih kelas yang memiliki frekuensi relatif terbesar 2. Kita tentukan tepi bawah dari nilai minimum kelas Modus Tepi bawah = = BB Kelas Modus 0,5 = 73 0,5 = 72,5 Kelas Modus
- 26. Modus Data Berkelompok 3. Kita tentukan nilai interval 3. Kita tentukan nilai b1 dengan menghitung selisih fi kelas Modus dengan nilai fi kelas sebelumnya Interval = C = ( BA BB ) +1 = ( 77 73 ) + 1 = 5 d1 = fi ( Modus ) - fi ( Modus 1 ) = 12 10 = 2
- 27. Modus Data Berkelompok 5. Kita tentukan nilai b2 dengan menghitung selisih fi kelas Modus dengan nilai fi kelas setelahnya 5. Menghitung Modus dengan rumus Modus untuk data berkelompok d2 = fi ( Modus ) - fi ( Modus + 1 ) = 12 7 = 5 = + 1 1 + 2
- 28. Kuartil Nilai yang membagi data menjadi 4 bagian Kuartil Data Tunggal Perhitungan kuartil untuk data tunggal menggunakan rumus sebagai berikut : i = menunjukkan kuartil ke berapa yang hendak dihitung n = jumlah individu frekuensi Contoh Soal Kuartil Data Tunggal Diketahui data sebagai berikut : 3, 3, 4, 5, 5, 5, 7, 8, 9, 9 . Tentukan Kuartil ke-3 !
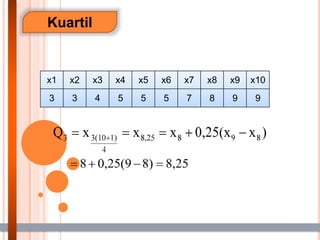
- 29. Kuartil x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 3 3 4 5 5 5 7 8 9 9
- 30. Kuartil Kuartil Data Berkelompok Perhitungan kuartil untuk data berkelompok menggunakan rumus sebagai berikut : i = menunjukkan Kuartil ke berapa yang hendak dihitung n = jumlah individu frekuensi = frekuensi kelas kuartil = frekuensi kumulatif sebelum kelas yang dimaksud = tepi bawah = ( BB 0,5 ) C = interval/panjang kelas = BA BB + 1 = + 4
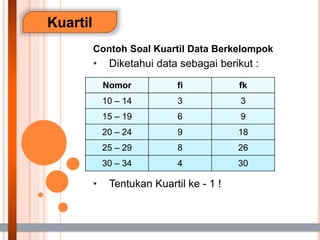
- 31. Kuartil Contoh Soal Kuartil Data Berkelompok Diketahui data sebagai berikut : Tentukan Kuartil ke - 1 ! Nomor fi fk 10 14 3 3 15 19 6 9 20 24 9 18 25 29 8 26 30 34 4 30
- 32. Kuartil 1. Kita tentukan kelas Kuartil 1 ( Q1 ) 1. Kita hitung nilai Kuartil 1 ( Q1 ) Nomor fi fk 10 14 3 3 15 19 6 9 20 24 9 18 25 29 8 26 30 34 4 30 data ke 7,5 terletak di kelas ke 2 1 = + 4 1
- 33. Desil Nilai yang membagi data menjadi 10 bagian Desil Data Tunggal Perhitungan desil untuk data tunggal menggunakan rumus sebagai berikut : i = menunjukkan desil ke berapa yang hendak dihitung n = jumlah individu frekuensi i = 1, 2 , 3, 4, .....9
- 34. Desil Contoh Soal Desil Data Tunggal Diketahui data sebagai berikut : 3, 3, 4, 5, 5, 5, 7, 8, 9, 9 . Tentukan Desil ke-7 ! x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 3 3 4 5 5 5 7 8 9 9
- 35. Desil Desil Data Berkelompok Perhitungan desil untuk data berkelompok menggunakan rumus sebagai berikut : i = menunjukkan Desill ke berapa yang hendak dihitung n = jumlah individu frekuensi = frekuensi kelas Desil = frekuensi kumulatif sebelum kelas yang dimaksud = tepi bawah = ( BB 0,5 ) C = interval/panjang kelas = BA BB + 1 倹 = + 10 倹 倹
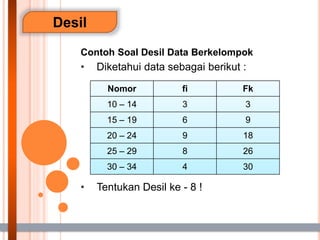
- 36. Desil Contoh Soal Desil Data Berkelompok Diketahui data sebagai berikut : Tentukan Desil ke - 8 ! Nomor fi Fk 10 14 3 3 15 19 6 9 20 24 9 18 25 29 8 26 30 34 4 30
- 37. Desil 1. Kita tentukan kelas Desil 8 ( D8 ) 1. Kita hitung nilai Desil 8 ( D8 ) Nomor fi Fk 10 14 3 3 15 19 6 9 20 24 9 18 25 29 8 26 30 34 4 30 data ke 24 terletak di kelas ke 4 8 = + 10 8
- 38. PERTANYAAN?
- 39. 1. Tentukan simpangan rata-rata, variansi, dan simpangan baku (standart deviasi) dari data tunggal berikut. a. 11, 13, 14, 16, 17, 18, 19, 20 b. 102, 105, 103, 106, 104, 102, 101, 105, 102 2. Dari tabel data kelompok berikut ini. Tentukanlah simpangan rata-rata, variansi, dan simpangan baku (standart deviasi) ! TUGAS KELOMPOK Berat (kg) frekuensi 31-36 4 37-42 6 43-48 9 49-54 14 55-60 10 61-66 5 67-72 2
- 40. Ketentuan tugas kelompok : 1. Ditulis tangan di kertas folio bergaris. 2. Di kumpulkan selambatnya hari selasa tanggal 12 Mei 2023 jam 13.00 (saat kuliah). 3. Tuliskan nama anggota kelompok (Nama, NIM, Kelas). 4. Jumlah anggota kelompok maksimal 3 orang.
- 41. Terima
Editor's Notes
- #3: Tujuan pemusatan data adalah membandingkan 2 populasi atau contoh. Karena sulit untuk membandingkan masing-masing anggota dari masing-masing anggota populasi.
- #4: Tujuan pemusatan data adalah membandingkan 2 populasi atau contoh. Karena sulit untuk membandingkan masing-masing anggota dari masing-masing anggota populasi.
- #7: Ada beberapa data nantinya yang tdk cocok menggunakan rumus ini
- #8: Ada beberapa data nantinya yang tdk cocok menggunakan rumus ini
- #9: Ada beberapa data nantinya yang tdk cocok menggunakan rumus ini