狠狠撸

Union-Find
（素集合データ構造）

? グループ分けを管理する
? はじめ，? 個の物は全て別々のグループ
? 次の 2 種類のクエリに対応する
1. 「まとめる」
2. 「判定」
Union-Find 木の機能
1 2 3 4 5

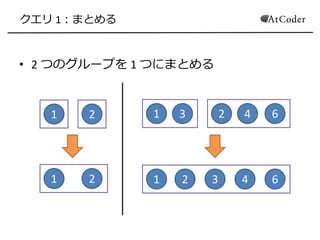
クエリ 1：まとめる
? 2 つのグループを 1 つにまとめる
1 2
1 2
1 3 2 4 6
1 2 3 4 6

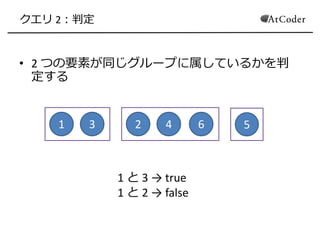
クエリ 2：判定
? 2 つの要素が同じグループに属しているかを判
定する
1 3 2 4 6 5
1 と 3 → true
1 と 2 → false

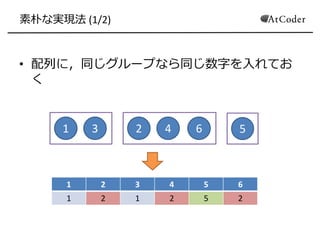
素朴な実現法 (1/2)
? 配列に，同じグループなら同じ数字を入れてお
く
1 3 2 4 6 5
1 2 3 4 5 6
1 2 1 2 5 2

素朴な実現法 (2/2)
? この方針の問題点
– グループをまとめる際に，?(?) 時間かかってしまう
– 実際には，この方針でも少しの工夫でならし ?(log ?) 時間にできます
http://topcoder.g.hatena.ne.jp/iwiwi/20131226/1388062106
? Union-Find 木は，もっと効率的に行う

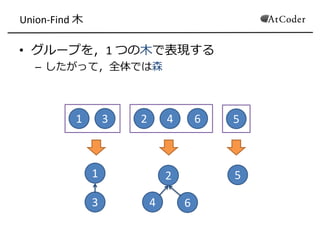
Union-Find 木
? グループを，1 つの木で表現する
– したがって，全体では森
1 3 2 4 6 5
1
3
2
4 6
5

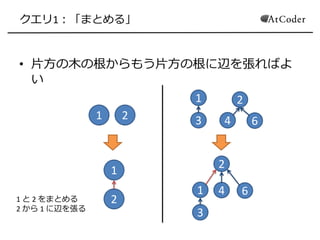
クエリ1：「まとめる」
? 片方の木の根からもう片方の根に辺を張ればよ
い
1 2
1
2
1
3
2
4 6
1
3
2
4 6
1 と 2 をまとめる
2 から 1 に辺を張る

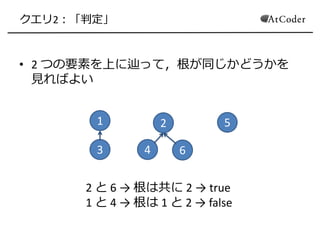
クエリ2：「判定」
? 2 つの要素を上に辿って，根が同じかどうかを
見ればよい
1
3
2
4 6
5
2 と 6 → 根は共に 2 → true
1 と 4 → 根は 1 と 2 → false

Union-Find 木の効率
? 正当性：このやり方で，グループの判定はうま
くできる
? 効率：最悪の場合，この方法でも
ツリーが縦長になると処理が遅く
なってしまう
→ 効率化のテクニックを導入

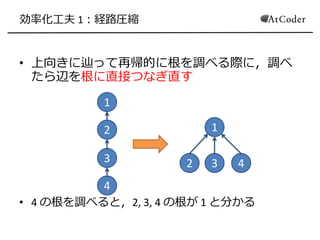
効率化工夫 1：経路圧縮
? 上向きに辿って再帰的に根を調べる際に，調べ
たら辺を根に直接つなぎ直す
? 4 の根を調べると，2, 3, 4 の根が 1 と分かる
1
2
3
4
1
2 3 4

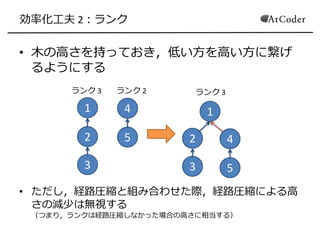
効率化工夫 2：ランク
? 木の高さを持っておき，低い方を高い方に繋げ
るようにする
? ただし，経路圧縮と組み合わせた際，経路圧縮による高
さの減少は無視する
（つまり，ランクは経路圧縮しなかった場合の高さに相当する）
1
2
3
4
5
1
2
3
4
5
ランク 3 ランク 2 ランク 3

Union-Find 木の計算量
? 2 つの工夫の両方をして ?(?(?))
– ?(?) はアッカーマン関数 ?(?, ?) の逆関数
– 相当小さい（log より小さい！）
? 片方だけでも，だいたい ?(log ?)
– 経路圧縮のみが実装が楽でよい
? これらはならし計算量

Union-Find 木の実装（ランク無し）
? 経路圧縮のみ（ランクは使わない）
? par[i] = i ならば根
– はじめは全部の頂点が根
int par[MAX_N]; // 親の番号
// n 要素で初期化
void init(int n) {
for (int i = 0; i < n; i++) par[i] = i;
}

// 木の根を求める
int root(int x) {
if (par[x] == x) { // 根
return x;
} else {
return par[x] = root(par[x]); // 経路圧縮
}
}
// x と y が同じ集合に属するか否か
bool same(int x, int y) {
return root(x) == root(y);
}

// x と y の属する集合を併合
void unite(int x, int y) {
x = root(x);
y = root(y);
if (x == y) return;
par[x] = y;
}

Union-Find 木の実装（ランク有り）
int par[MAX_N], rank[MAX_N];
void init(int n) {
for (int i = 0; i < n; i++) {
par[i] = i;
rank[i] = 0;
}
}
int root(int x) {
return par[x] == x ? x : par[x] =
root(par[x]);
}
bool same(int x, int y) {
return root(x) == root(y);
}
void unite(int x, int y) {
x = root(x);
y = root(y);
if (x == y) return;
if (rank[x] < rank[y]) {
par[x] = y;
} else {
par[y] = x;
if (rank[x] == rank[y]) rank[x]++;
}
}

補足
? Union-Find 木はグループをまとめることはでき
ても，分割することはできない
重要な制約
? Union-Find 木を改造して機能を付加することが
必要になるような問題もあります

狠狠撸

Union find(素集合データ構造)

More Related Content

Union find(素集合データ構造)