Unit 1.6
- 1. 1.6 Graphical Transformations Copyright ÂĐ 2011 Pearson, Inc.
- 2. What youâll learn about ïŪ Transformations ïŪ Vertical and Horizontal Translations ïŪ Reflections Across Axes ïŪ Vertical and Horizontal Stretches and Shrinks ïŪ Combining Transformations âĶ and why Studying transformations will help you to understand the relationships between graphs that have similarities but are not the same. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 2
- 3. Transformations In this section we relate graphs using transformations, which are functions that map real numbers to real numbers. Rigid transformations, which leave the size and shape of a graph unchanged, include horizontal translations, vertical translations, reflections, or any combination of these. Nonrigid transformations, which generally distort the shape of a graph, include horizontal or vertical stretches and shrinks. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 3
- 4. Vertical and Horizontal Translations Let c be a positive real number. Then the following transformations result in translations of the graph of y = f(x). Horizontal Translations y = f(x â c) a translation to the right by c units y = f(x + c) a translation to the left by c units Vertical Translations y = f(x) + c a translation up by c units y = f(x) â c a translation down by c units Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 4
- 5. Example Vertical Translations Describe how the graph of f (x) ï― x can be transformed to the graph of y ï― x ï 4. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 5
- 6. Solution Describe how the graph of f (x) ï― x can be transformed to the graph of y ï― x ï 4. It is a translation down by 4 units. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 6
- 7. Example Finding Equations for Translations Each view shows the graph of y1 ï― x3 and a vertical or horizontal translation y2 . Write an equation for y2 . Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 7
- 8. Solution Each view shows the graph of y1 ï― x3 and a vertical or horizontal translation y2 . Write an equation for y2 . (a) y2 ï― x3 ï 3 (b) y2 ï― ïĻx ïŦ 2ïĐ3 (c) y2 ï― ïĻx ï 3ïĐ3 Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 8
- 9. Reflections The following transformations result in reflections of the graph of y = f(x): Across the x-axis y = âf(x) Across the y-axis y = f(âx) Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 9
- 10. Graphing Absolute Value Compositions Given the graph of y = f(x), the graph y = |f(x)| can be obtained by reflecting the portion of the graph below the x-axis across the x-axis, leaving the portion above the x-axis unchanged; the graph of y = f(|x|) can be obtained by replacing the portion of the graph to the left of the y-axis by a reflection of the portion to the right of the y-axis across the y-axis, leaving the portion to the right of the y-axis unchanged. (The result will show even symmetry.) Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 10
- 11. Stretches and Shrinks Let c be a positive real number. Then the following transformations result in stretches or shrinks of the graph of y ï― f (x): Horizontal Stretches or Shrinks y ï― f x c ïĶ ïĻ ï§ ïķ ïļ ï· a stretch by a factor of c if c ïū 1 a shrink by a factor of c if c ïž 1 ïŽ ï ïŪ Vertical Stretches or Shrinks y ï― c ï f (x) a stretch by a factor of c if c ïū 1 a shrink by a factor of c if c ïž 1 ïŽ ï ïŪ Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 11
- 12. Example Finding Equations for Stretches and Shrinks Let C1 be the curve defined by y1 ï― x3 ïŦ 3. Find equations for the following non-rigid transformations of C1 : (a) C2 is a vertical stretch of C1 by a factor of 4. (b) C3 is a horizontal shrink of C1 by a factor of 1/3. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 12
- 13. Solution Let C1 be the curve defined by y1 ï― x3 ïŦ 3. Find equations for the following non-rigid transformations of C1 : (a) C2 is a vertical stretch of C1 by a factor of 4. (b) C3 is a horizontal shrink of C1 by a factor of 1/3. (a) y2 ï― 4 ï f (x) ï― 4(x3 ïŦ 3) ï― 4x3 ïŦ 12 (b) y3 ï― f x 1 / 3 ïĶ ïĻ ï§ ïķ ïļ ï· ï― f (3x) ï― (3x)3 ïŦ 3 ï― 27x3 ïŦ 3 Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 13
- 14. Example Combining Transformations in Order The graph of y ï― x2 undergoes the following transformations, in order. Find the equation of the graph that results. ï· a horizontal shift 5 units to the left ï· a vertical stretch by a factor of 3 ï· a vertical translation 4 units up Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 14
- 15. Solution The graph of y ï― x2 undergoes the following transformations, in order. Find the equation of the graph that results. ï· a horizontal shift 5 units to the left ï· a vertical stretch by a factor of 3 ï· a vertical translation 4 units up x2 ïïĻx ïŦ 5ïĐ2 ï3ïĻx ïŦ 5ïĐ2 ï3ïĻx ïŦ 5ïĐ2 ïŦ 4 Expanding the final expression: y ï― 3x2 ïŦ 30x ïŦ 79 Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 15
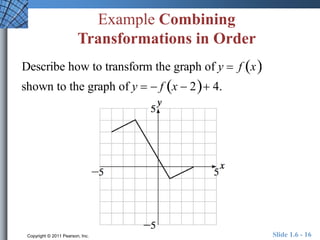
- 16. Example Combining Transformations in Order Describe how to transform the graph of y ï― f ïĻxïĐ shown to the graph of y ï― ï f ïĻx ï 2ïĐïŦ 4. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 16
- 17. Solution Describe how to transform the graph of y ï― f ïĻxïĐ shown to the graph of y ï― ï f ïĻx ï 2ïĐïŦ 4. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 17
- 18. Solution (continued) Describe how to transform the graph of y ï― f ïĻxïĐ shown to the graph of y ï― ï f ïĻx ï 2ïĐïŦ 4. Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 18
- 19. Quick Review Write the expression as a binomial squared. 1. x2 ïŦ 4x ïŦ 4 2. x2 ï 2x ïŦ 1 3. 4x2 ïŦ 36x ïŦ 81 Perform the indicated operations and simplify. 4. (x ï 1)2 ïŦ (x ï 1) ïŦ 2 5. (x ï 1)3 ïŦ (x ï 1) ïŦ 2 Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 19
- 20. Quick Review Solutions Write the expression as a binomial squared. 1. x2 ïŦ 4x ïŦ 4 (x ïŦ 2)2 2. x2 ï 2x ïŦ 1 (x ï 1)2 3. 4x2 ïŦ 36x ïŦ 81 (2x ïŦ 9)2 Perform the indicated operations and simplify. 4. (x ï 1)2 ïŦ (x ï 1) ïŦ 2 x2 ï x ïŦ 2 5. (x ï 1)3 ïŦ (x ï 1) ïŦ 2 x3 ï 3x2 ïŦ 4x Copyright ÂĐ 2011 Pearson, Inc. šÝšÝßĢ 1.6 - 20