Unit 3: Classical information
Download as PPTX, PDF
0 likes82 views
This document discusses classical information theory and concepts like entropy. It defines entropy as quantifying the apparent disorder of particles in a room. Different examples of sequences are provided, from a highly ordered repeating sequence to a more random typical sequence. Functions are defined to calculate the string length and characters of a given sequence. The document also shows how to calculate the entropy of a sequence and compares the results of different entropy calculation functions.
![Classical Information Theory
sequence = "this is not a sentence"
StringLength[sequence]
22
Characters[sequence]
{"t", "h", "i", "s", " ", "i", "s", " ", "n", "o", "t", " ", "a", " ", "s",
"e", "n", "t", "e", "n", "c", "e"}](https://image.slidesharecdn.com/classicalinformation-180926154547/85/Unit-3-Classical-information-8-320.jpg)
![Classical Information Theory
{3/22, 1/22, 1/11, 3/22, 2/11, 3/22, 1/22, 1/22, 3/22, 1/22}
MyEntropy[base_, s_] :=
N@Total[Table[-Log[base, #[[i, 2]]/Total[Last /@ #]] (#[[i, 2]]/
Total[Last /@ #]), {i, Length[#]}] &@Tally[Characters@s]]
MyEntropy[2, sequence]
3.14036](https://image.slidesharecdn.com/classicalinformation-180926154547/85/Unit-3-Classical-information-10-320.jpg)
![Classical Information Theory
1 <= x <= N
Log2 N
O Log2 N
N@Log[2, 100]
6.64386](https://image.slidesharecdn.com/classicalinformation-180926154547/85/Unit-3-Classical-information-12-320.jpg)
![Classical Information Theory
(1) between 1 and 50? In this case, yes
(2) between 1 and 25? Yes
(3) between 1 and 13? No
(4) between 14 and 20? Yes
(5) between 14 and 17? Yes
(6) between 16 and 17? Yes
(7) is it 16? No
N@Entropy[2, sequence]
MyEntropy[sequence] == Entropy[sequence]
True](https://image.slidesharecdn.com/classicalinformation-180926154547/85/Unit-3-Classical-information-13-320.jpg)
Unit 3: Classical information
- 2. Classical Information Theory Entropy is defined to quantify the apparent disorder of a room with particles Statistical information on the average behaviour A way to study particles is by using symbols forming objects such as sequences or messages
- 3. Classical Information Theory Looks highly ordered: s = 1111111111111111111111111111111111111111111111111 1
- 4. Classical Information Theory Looks highly ordered: s = 1111111111111111111111111111111111111111111111111 1 Looks less ordered: s = 0011010000110011000011000000110111110101010010100 0 Looks more typical because it is the kind of sequence one
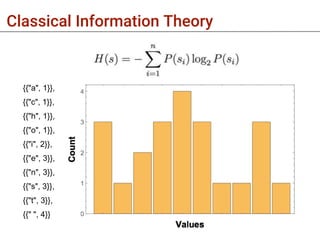
- 8. Classical Information Theory sequence = "this is not a sentence" StringLength[sequence] 22 Characters[sequence] {"t", "h", "i", "s", " ", "i", "s", " ", "n", "o", "t", " ", "a", " ", "s", "e", "n", "t", "e", "n", "c", "e"}
- 9. Classical Information Theory {{"a", 1}}, {{"c", 1}}, {{"h", 1}}, {{"o", 1}}, {{"i", 2}}, {{"e", 3}}, {{"n", 3}}, {{"s", 3}}, {{"t", 3}}, {{" ", 4}}
- 10. Classical Information Theory {3/22, 1/22, 1/11, 3/22, 2/11, 3/22, 1/22, 1/22, 3/22, 1/22} MyEntropy[base_, s_] := N@Total[Table[-Log[base, #[[i, 2]]/Total[Last /@ #]] (#[[i, 2]]/ Total[Last /@ #]), {i, Length[#]}] &@Tally[Characters@s]] MyEntropy[2, sequence] 3.14036
- 12. Classical Information Theory 1 <= x <= N Log2 N O Log2 N N@Log[2, 100] 6.64386
- 13. Classical Information Theory (1) between 1 and 50? In this case, yes (2) between 1 and 25? Yes (3) between 1 and 13? No (4) between 14 and 20? Yes (5) between 14 and 17? Yes (6) between 16 and 17? Yes (7) is it 16? No N@Entropy[2, sequence] MyEntropy[sequence] == Entropy[sequence] True